Тема 9. индексы
Содержание задания и требования к нему
Расчеты по задаче должны быть выполнены с приведением формул в развернутом виде, сопровождаться пояснениями и описанием результатов.
Исходные данные
| Вариант | Продукты | Единицы измерения | Продано товаров, тыс. ед. | Цена реализации за ед., руб. | ||
| Базисный период | Отчетный период | Базисный период | Отчетный период | |||
| А Б В | кг л шт. | 42,0 38,0 13,5 | 44,0 39,5 14,0 | |||
| А Б В | кг л шт. | 51,5 49,5 15,5 | 52,0 50,5 16,5 | |||
| А Б В | кг л шт. | 40,0 50,0 14,5 | 42,0 55,0 14,5 | |||
| А Б В | кг л шт. | 63,0 78,0 17,0 | 63,5 79,0 17,5 | |||
| А Б В | кг л шт. | 92,5 88,5 16,5 | 93,0 88,9 17,0 | |||
| А Б В | кг л шт. | 32,0 18,0 3,5 | 34,0 19,5 4,0 | |||
| А Б В | кг л шт. | 41,5 19,5 5,5 | 42,0 20,5 6,5 | |||
| А Б В | кг л шт. | 40,0 30,0 4,5 | 42,0 35,0 4,5 | |||
| А Б В | кг л шт. | 43,0 28,0 7,0 | 43,5 29,0 7,5 | |||
| А Б В | кг л шт. | 42,5 28,5 6,5 | 43,0 28,9 7,0 |
На основе соответствующих вашему варианту данных определить:
1) индивидуальные индексы физического объема реализации, цен и товарооборота;
2) сводный индекс цен (Пааше);
3) сводный индекс физического объема реализации;
4) сводный индекс товарооборота;
5) абсолютное изменение товарооборота в отчетном периоде по сравнению с базисным всего, в том числе за счет изменения цен и физического объема реализации.
Показать взаимосвязь полученных результатов.
Методические указания к выполнению задания по теме 9
В статистике индексами называют относительные показатели, характеризующие соотношение явлений во времени, в пространстве или по сравнению с некоторым эталоном (планируемым, нормативным уровнем и т.п.).
Индексы делятся на индивидуальные и общие (сводные).
Индивидуальный индекс характеризует изменение отдельных элементов той или иной совокупности. Так, индивидуальный индекс цены рассчитывается по формуле
,
где р 1 – цена товара в текущем периоде;
р 0 – цена товара в базисном периоде.
Например, если цена товара А в текущем периоде составляла 30 руб., а в базисном 25 руб., то индивидуальный индекс цены равен
1,2 или 120%.
В данном примере цена товара А возросла по сравнению с базисным уровнем в 1,2 раза или на 20%.
Сводный индекс – это сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из непосредственно несоизмеримых элементов. Исходной формой сводного индекса является агрегатная.
При расчете агрегатного индекса для разнородной совокупности находят такой общий показатель, в котором можно объединить все ее элементы. Например, цены различных товаров складывать неправомерно, однако с экономической точки зрения вполне допустимо суммировать товарооборот по этим товарам. Если мы сравним товарооборот в текущем периоде с его величиной в базисном периоде, то получим сводный индекс товарооборота:
.
На величину данного индекса оказывают влияние как изменение цен, так и изменение объемов реализации. Чтобы оценить изменение только цен (индексируемой величины), необходимо количество проданных товаров (веса индекса) зафиксировать на каком-либо постоянном уровне. Если в качестве веса используют объемный показатель, его обычно фиксируют на уровне текущего периода. Таким способом получают сводный индекс цен (по методу Пааше):
.
Третьим индексом в данной индексной системе является сводный индекс физического объема реализации:
.
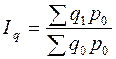Весами в данном индексе выступают цены, которые фиксируются на базисном уровне.
Между рассчитанными индексами существует следующая взаимосвязь:
Ip·Iq = Ipq.
Пример. На основе следующих данных рассчитать сводные индексы доходов, цен и объема перевозок:
| Род груза | Объем перевозок, млн. ткм | Доходная ставка, коп./10 ткм | Расчетные графы, тыс. руб. | ||||
база
| отчет
| база
| отчет
| 
| 
| 
| |
| Руда Уголь Нефть | 126,484 58,425 138,421 | 129,135 59,274 140,345 | 10118,7 5842,5 10381,6 | 9685,1 5631,0 12631,1 | 9486,3 5550,4 12457,9 | ||
| Итого | – | – | – | – | 26342,8 | 27947,2 | 27494,6 |
Решение:
1,061 или 106,1%.
Мы получили, что доходы от перевозок данных грузов в текущем периоде по сравнению с базисным увеличились на 6,1% (106,1 – 100).
1,016 или 101,6%.
По данной группе грузов доходные ставки в текущем периоде по сравнению с базисным в среднем выросли на 1,6%.
Числитель и знаменатель сводного индекса цен можно интерпретировать с точки зрения потребителей транспортных услуг. Числитель представляет собой сумму денег, фактически уплаченных грузовладельцами за перевезенные в текущем периоде грузы. Знаменатель же показывает, какую сумму грузовладельцы заплатили бы за перевозку тех же грузов, если бы доходные ставки не изменились. Разность числителя и знаменателя будет отражать величину экономии (знак "–") или перерасхода (знак "+") грузоотправителей от изменения цен на перевозку:
= 27947,2 – 27494,6 = +452,6 тыс. руб. – перерасход.
1,044 или 104,4%.
Объем перевозок в целом по данной группе грузов увеличился на 4,4%.
Используя взаимосвязь индексов, проверим правильность вычислений:
= 1,016·1,044 = 1,061 или 106,1%.
Для определения общего изменения уровня себестоимости нескольких видов продукции, выпускаемых предприятием, рассчитывается сводный индекс себестоимости. При этом себестоимость взвешивается по объему производства отдельных видов продукции текущего периода:
.
Числитель этого индекса отражает затраты на производство текущего периода, а знаменатель – условную величину затрат при сохранении себестоимости на базисном уровне. Разность числителя и знаменателя показывает сумму экономии предприятия от снижения себестоимости:
.
Сводный индекс физического объема продукции, взвешенный по себестоимости, имеет следующий вид:
.
Третьим показателем в данной индексной системе является сводный индекс затрат на производство:
.
Все три индекса взаимосвязаны между собой: 
.
Еще одна область применения индексного метода – анализ изменений в производительности труда. Индивидуальные индексы производительности труда имеют вид:
,
где t – затраты рабочего времени на единицу продукции.
Трудоемкость является обратным показателем, поэтому снижение трудоемкости в текущем периоде по сравнению с базисным свидетельствует о росте производительности труда.
Располагая данными о трудоемкости различных видах продукции и объемах их производства, можно рассчитать сводный индекс производительности труда:
.
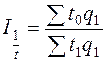Разность знаменателя и числителя этого индекса показывает сумму экономии затрат труда за счет роста производительности труда.
Сводный индекс физического объема продукции, взвешенный по трудоемкости, имеет следующий вид:
.
Третьим показателем в данной индексной системе является сводный индекс затрат труда (массы отработанного времени):
.
Все три индекса взаимосвязаны между собой:
.
В ряде случаев на практике вместо индексов в агрегатной форме удобнее использовать средние арифметические и средние гармонические индексы.
Предположим, мы располагаем данными о стоимости проданной продукции в текущем периоде (
) и индивидуальными индексами цен 
. Тогда в знаменателе сводного индекса цен 
можно использовать следующую замену:
.
Таким образом, сводный индекс цен будет выражен в форме средней гармонической из индивидуальных индексов:
.
Например, требуется получить сводную оценку изменения тарифов по имеющимся данным:
| Род груза | Сумма доходов в текущем периоде, тыс.руб. p1q1 | Изменение тарифа в текущем периоде по сравнению с базисным, % | Расчетные графы | |
| 
| |||
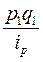
| Лесоматериалы Нефтепродукты Торф | +4,0 +2,3 -0,8 | 1,04 1,023 0,992 | ||
| Итого | – | – |
Вычислим средний гармонический индекс:
1,016 или 101,6%.
Тарифы по данной группе грузов в текущем периоде по сравнению с базисным в среднем возросли на 1,6%.
При расчете сводного индекса физического объема продукции 
можно использовать среднюю арифметическую форму. При этом в числителе производится замена 
= 
. Тогда индекс примет вид:
.
Например, необходимо рассчитать сводный индекс объема перевозок по следующим данным:
| Род груза | Доходы от перевозок в базисном периоде,
тыс. руб.
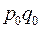
| Изменение объема перевозок в текущем периоде по сравнению с базисным, % | Расчетные графы | |
|  
| |||
| Кирпич Цемент Удобрения | –6,4 –8,2 +1,3 | 0,936 0,918 1,013 | ||
| Итого | – | – |
Рассчитаем средний арифметический индекс:
0,964 или 96,4%.
Таким образом, объем перевозок по данной группе грузов в среднем снизился на 3,6%.