Министерство сельского хозяйства Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«Саратовский государственный университет
Имени Н.И. Вавилова»
Дифференциальные уравнения
первого порядка
Саратов
ВВЕДЕНИЕ
В учебно-методических указаниях рассмотрены три вида дифференциальных уравнений первого порядка: дифференциальные уравнения с разделяющимися переменными, однородные и линейные дифференциальные уравнения, которые изучаются студентами технических специальностей вузов. Кратко излагается теоретический материал с разбором типовых примеров. Составлены задания для самостоятельного решения.
Дифференциальные уравнения имеют широкие применения в классической механике, математической экономике, математическом анализе и многих других разделах естествознания.
Опираясь на многолетний опыт работы, авторы попытались создать универсальное учебно-методическое указание, пригодное как для самообразования, так и для активной работы с преподавателем на практических занятиях.
Работа содержит пять разделов, каждый из которых включает в себя необходимый теоретический материал, решения типовых задач.
Цель работы: усвоение методов и приобретение практических навыков в решении обыкновенных дифференциальных уравнений первого порядка.
Основные понятия
Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту ил иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков.
В качестве примера можно рассмотреть простейший случай равноускоренного движения материальной точки.
Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:
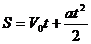
В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения S. Т.е.
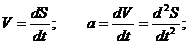
Тогда получаем: 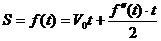 - уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t).
- уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t).
Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную х, искомую функцию y=f(x) и ее производную y'.
В общем случае дифференциальное уравнение первого порядка можно записать так
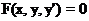 (1.1)
(1.1)
Решением или интегралом дифференциального уравнения называется всякая функция y=f(x), которая будучи подставлена в уравнение, превращает его в тождество.
Рассмотрим пример.
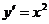 (1.2)
(1.2)
Путем интегрирования найдем
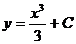 (1.3)
(1.3)
Выражение (1.3) является общим решением уравнения (1.2). Давая постоянной 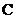 конкретные численные значения, получим частные решения уравнения (1.2).
конкретные численные значения, получим частные решения уравнения (1.2).
Очень часто общее решение получается в неявной форме
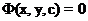 (1.4)
(1.4)
Соотношение (1.4) называется общим интегралом. Чтобы из общего решения выделить одно частное, требуется к дифференциальному уравнению присоединить начальное условие.
Условие, что при 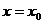 функция
функция 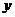 должна равняться заданному числу
должна равняться заданному числу 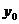 , называется начальным условием. Оно записывается в виде:
, называется начальным условием. Оно записывается в виде:
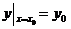 или
или 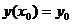 .
.
Задача о нахождении частного решения дифференциального уравнения при заданных начальных условиях есть начальная задача или задача Коши.
Задачей Коши называется нахождение любого частного решения дифференциального уравнения вида 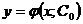 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 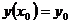 .
.
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка) Если функция 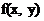 непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную
непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную 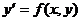 , то какова бы не была точка
, то какова бы не была точка 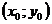 в области D, существует единственное решение
в области D, существует единственное решение 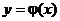 уравнения
уравнения 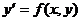 , определенное в некотором интервале, содержащем точку
, определенное в некотором интервале, содержащем точку 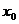 , принимающее при
, принимающее при 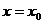 значение
значение 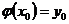 , т.е. существует единственное решение дифференциального уравнения.
, т.е. существует единственное решение дифференциального уравнения.
Интегралом дифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием. 
Интегральной кривой называется график 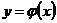 решения дифференциального уравнения на плоскости ХОY.
решения дифференциального уравнения на плоскости ХОY.
Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши не выполняется, т.е. в окрестности некоторой точки 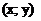 существует не менее двух интегральных кривых. Особые решения не зависят от постоянной С.
существует не менее двух интегральных кривых. Особые решения не зависят от постоянной С.
Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Вопросы для самоконтроля
1. Обыкновенные дифференциальные уравнения.
2. Теорема Коши о существовании и единственности решения дифференциального уравнения 1- го порядка.
3. Геометрический смысл дифференциального уравнения 1- го порядка.
4. Особые решения дифференциального уравнения.
2. Дифференциальные уравнения
с разделяющимися переменными
Дифференциальное уравнение с разделяющимися переменными имеет вид
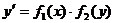 (2.1)
(2.1)
Отсюда
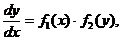
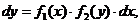
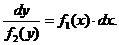 (2.2)
(2.2)
Переменные разделились (считаем, что f2(y)≠0). Равенство (2.2) можно рассматривать как равенство двух дифференциалов, а неопределенные интегралы от них будут тогда отличаться на постоянное слагаемое. Очевидно, общий интеграл его есть
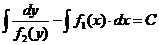 (2.3)
(2.3)
Уравнения вида 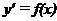 .
.
Пусть функция 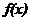 – определена и непрерывна на некотором интервале
– определена и непрерывна на некотором интервале 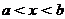 . В таком случае все решения данного дифференциального уравнения находятся как
. В таком случае все решения данного дифференциального уравнения находятся как 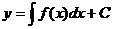 . Если заданы начальные условия
. Если заданы начальные условия 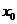 и
и 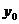 , то можно определить постоянную С.
, то можно определить постоянную С.
Пример 1. Найти общее решение уравнения
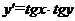 .
.
Решение. Записываем
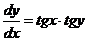 ,
,
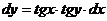 (2.4)
(2.4)
Полагая, что 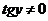 , разделим обе части равенства на
, разделим обе части равенства на 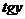 :
:
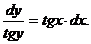
Проинтегрируем последнее выражение
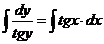 ,
,
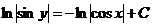 ,
,
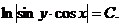
Это есть общий интеграл уравнения (2.4).
Иногда, для удобства записи, произвольную постоянную представляют как 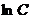 . Так, в последнем примере мы могли бы записать
. Так, в последнем примере мы могли бы записать

Тогда имели бы общее решение в виде
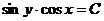
Пример 2. Найти частное решение дифференциального уравнения 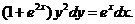 Начальное условие:
Начальное условие: 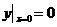
Решение. Делим обе части уравнения на 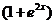 :
:
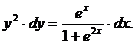
Переменные разделились. Интегрируя, находим:
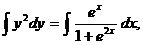
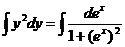 ,
,
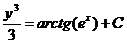
Или  - это есть общее решение исходного уравнения.
- это есть общее решение исходного уравнения.
Используя начальное уравнение, из общего решения найдем частное:
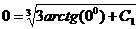 ,
,
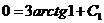 ,
,
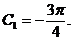
Частное решение: 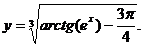
Замечание. Уравнения вида
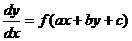 (2.5)
(2.5)
приводится к уравнениям с разделяющимися переменными заменой 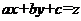 .
.
Пример 3. Решить уравнение
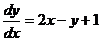 (2.6)
(2.6)
Решение. Обозначим
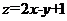 ,
,
тогда 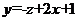 (2.7)
(2.7)
 (2.8)
(2.8)
Подставляя (2.7), (2.8) в (2.6), будем иметь
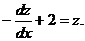
Разделим переменные:
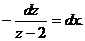
Проинтегрировав, получаем
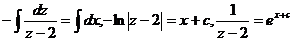
Учитывая (2.7), запишем общее решение дифференциального уравнения:
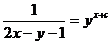
или
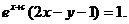
Вопросы для самоконтроля
1. Уравнения с разделяющимися переменными.
2. Уравнения вида 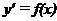 .
.
Однородные дифференциальные уравнения
Функция 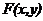 называется однородной степени
называется однородной степени  , если для всех
, если для всех  выполняется равенство
выполняется равенство 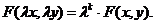
Например, 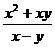 является однородной функцией степени 1.
является однородной функцией степени 1.
Действительно,
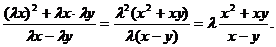
Функция 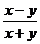 - однородная функция 0 - измерения, так как
- однородная функция 0 - измерения, так как
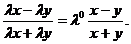
Дифференциальное уравнение
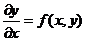 (3.1)
(3.1)
называется однородным, если 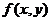 является однородной функцией 0-измерения.
является однородной функцией 0-измерения.
Является ли однородной функция 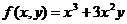 ?
?
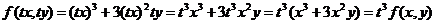
Таким образом, функция 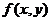 является однородной 3- го порядка.
является однородной 3- го порядка.
По условию 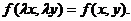 Положив
Положив 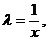 получим:
получим:
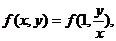
то есть однородная функция нулевого измерения зависит только от отношения аргументов.
Уравнение (3.1) примет вид
 (3.2)
(3.2)
Сделаем подстановку 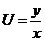 или
или 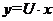 . Тогда
. Тогда 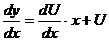 (как производная произведения). Уравнение (3.2) запишется сл. образом
(как производная произведения). Уравнение (3.2) запишется сл. образом
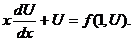
Это уравнение с разделяющимися переменными.
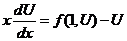 ,
,
 ,
,
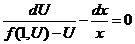 .
.
Интегрируя, найдем
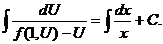
Подставляя после интегрирования вместо  отношение
отношение  , получим интеграл уравнения (3.1).
, получим интеграл уравнения (3.1).
Замечание. Однородное дифференциальное уравнение может быть записано в виде
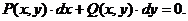 (3.3)
(3.3)
В этом случае 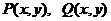 должны быть однородными функциями одного измерения.
должны быть однородными функциями одного измерения.
Пример 1. Найти общий интеграл уравнения
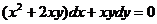 (3.4)
(3.4)
Решение. Здесь 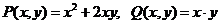 , обе функции однородные, второго измерения, так как
, обе функции однородные, второго измерения, так как
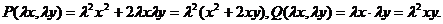
Введем подстановку 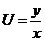
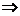
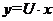 . Отсюда
. Отсюда
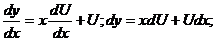
Уравнение (3.4) примет вид
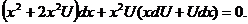 (3.5)
(3.5)
Раскрывая скобки, приводя подобные члены и сокращая на 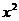 , получаем
, получаем 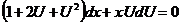 .
.
Разделяя переменные, интегрируя, заменяя 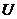 на
на 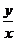 , находим общий интеграл уравнения (3.4).
, находим общий интеграл уравнения (3.4).
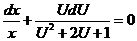 ,
,
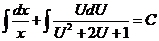 ,
,
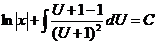 ,
,
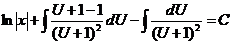 ,
,
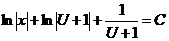 ,
,
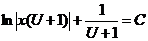 ,
,
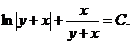
Пример 2. Найти частной решение уравнения
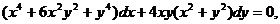 (3.5)
(3.5)
 (3.6)
(3.6)
Решение. Здесь 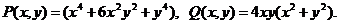
Обе функции - однородные четвертого измерения. Введем подстановку 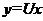
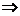
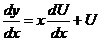 ,
, 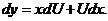
Уравнение (3.5) преобразуется к виду
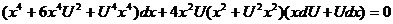 (3.7)
(3.7)
Раскрывая скобки, приводя подобные члены и сокращая на 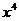 , приходим к уравнению с разделяющимися переменными:
, приходим к уравнению с разделяющимися переменными:
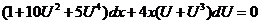 ,
,
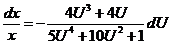 ,
,
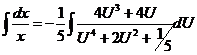 ,
,
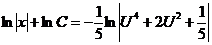 ,
,
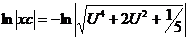 ,
,
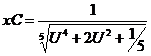 .
.
Заменяя 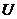 на
на 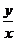 , получаем общий интеграл уравнения (3.5)
, получаем общий интеграл уравнения (3.5)
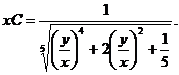
Для нахождения частного решения используем начальное условие (3.6)
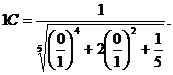
Таким образом, частное решение уравнения (3.5) запишется так:
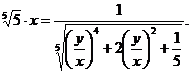
Преобразуем ответ:
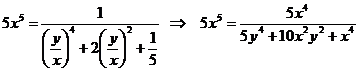 ,
,
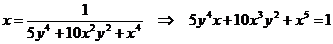 .
.
Вопросы для самоконтроля
1. Однородные функции однородные степени к.
2. Однородные дифференциальные уравнения.
4. Дифференциальные уравнения,
приводящиеся к однородным
Уравнение вида
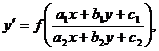 (4.1)
(4.1)
в зависимости от величины определителя 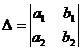 , приводится к однородным двумя способами. Если
, приводится к однородным двумя способами. Если 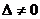 , то применяется подстановка
, то применяется подстановка 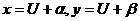 , где
, где 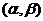 - точка пересечения прямых
- точка пересечения прямых 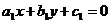 ,
, 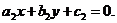 Если определитель равен нулю, то используется подстановка
Если определитель равен нулю, то используется подстановка 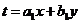 , которая позволяет разделить переменные.
, которая позволяет разделить переменные.
Пример 1. Решить уравнение
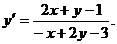 (4.2)
(4.2)
Решение. Составим определитель 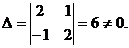
Найдем точку пересечения прямых
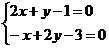 ,
, 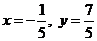 то есть
то есть 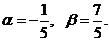
Применяя подстановку 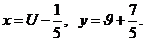 Тогда
Тогда 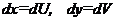 , а следовательно,
, а следовательно, 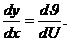
Уравнение (4.2) примет вид
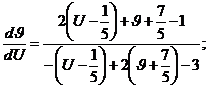 (4.3)
(4.3)
или
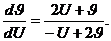 (4.4)
(4.4)
Пришли к однородному уравнению. Полагаем 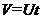 .
.
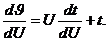 Подставляем данные выражения в уравнение (4.4)
Подставляем данные выражения в уравнение (4.4)
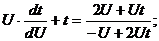
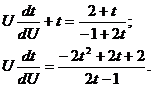
Разделяем переменные
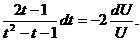
Интегрируем
 ,
,
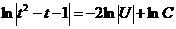 ,
,
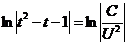 .
.
Применим логарифмическое свойство.
 (4.5)
(4.5)
Так как 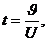 то выражение (4.5) запишется в виде
то выражение (4.5) запишется в виде
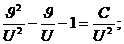
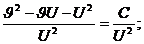
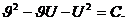 (4.6)
(4.6)
Но  следовательно,
следовательно,
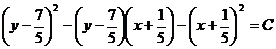
Раскрывая скобки и приводя подобные члены, приходим к общему интегралу уравнения (4.2):
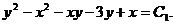
Пример 2. Найти общий интеграл уравнения
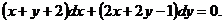 (4.7)
(4.7)
Решение. Данное уравнение можно записать в виде
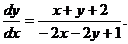 (4.8)
(4.8)
Составим определитель 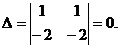
Применим подстановку 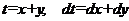 ,
, 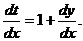
Уравнение (4.8) в новых переменных запишется так:

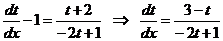 ,
,
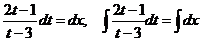 ,
,
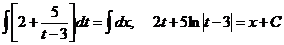 ,
,
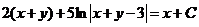 .
.
 - общий интеграл уравнения (4.7).
- общий интеграл уравнения (4.7).