Фильтр Калмана основан на дискретизированных по времени линейных динамических системах. Такие системы можно смоделировать с помощью Марковских цепей при помощи линейных операторов и слагаемых с нормальным распределением [5]. Состояние системы описывается вектором конечной размерности — вектором состояния. В каждый такт времени линейный оператор действует на вектор состояния и переводит его в другой вектор состояния, добавляется некоторый вектор нормального шума и в общем случае вектор управления, моделирующий воздействие системы управления [6].
Вектор состояния содержит в себе компоненты интерферометрического сигнала, модель которого описана в первой главе. Набор параметров в уравнении (1) можно преобразовать в вектор состояния, он будет выглядеть следующим образом:
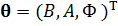 , (2)
, (2)
где 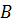 – компонента оценки фоновой составляющей сигнала,
– компонента оценки фоновой составляющей сигнала, 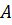 – компонента оценки амплитуды,
– компонента оценки амплитуды, 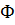 – компонента оценки фазы. Далее вводятся компоненты для оценивания всех необходимых составляющих сигнала: вектор компонентов
– компонента оценки фазы. Далее вводятся компоненты для оценивания всех необходимых составляющих сигнала: вектор компонентов 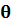 из уравнения (2), содержащий 3 элемента, описанных выше – оценки компонент амплитуды, фона и фазы. При инициализации алгоритма данные компоненты оценок представляют собой вектора, размерность которых соответствует размерности исходного сигнала, а начальные значения данных компонент равны нулю.
из уравнения (2), содержащий 3 элемента, описанных выше – оценки компонент амплитуды, фона и фазы. При инициализации алгоритма данные компоненты оценок представляют собой вектора, размерность которых соответствует размерности исходного сигнала, а начальные значения данных компонент равны нулю.
На k -ом шаге работы алгоритма вектор состояния рассчитывается по следующей формуле:
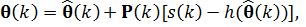 (3)
(3)
где 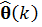 – предсказанное значение,
– предсказанное значение, 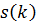 – значение исходного сигнала на k-ом шаге;
– значение исходного сигнала на k-ом шаге; 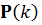 – матричный коэффициент усиления фильтра, определяющий вклад невязки наблюдения и предсказания в оценку вектора параметров. Коэффициент усиления
– матричный коэффициент усиления фильтра, определяющий вклад невязки наблюдения и предсказания в оценку вектора параметров. Коэффициент усиления 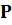 вычисляется следующим образом:
вычисляется следующим образом:
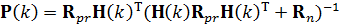 , (4)
, (4)
где 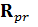 – предсказание ковариационной матрицы ошибок,
– предсказание ковариационной матрицы ошибок, 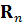 – ковариационная матрица шума наблюдения, а
– ковариационная матрица шума наблюдения, а 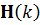 – матрица первых производных функции h (θ) по компонентам исходного сигнала [7]. Рассчитанная матрица H представлена следующим образом:
– матрица первых производных функции h (θ) по компонентам исходного сигнала [7]. Рассчитанная матрица H представлена следующим образом:
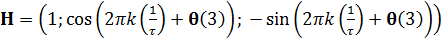 .(5)
.(5)
Компоненты предсказания ковариационной матрицы ошибок и ковариационной матрицы шума наблюдения, содержащиеся в уравнении (4), определяют вклад каждой оценки компоненты вектора параметров 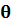 , то есть, какую из компонент вектора параметров фильтр обрабатывает в большей степени. Ковариационная матрица ошибок
, то есть, какую из компонент вектора параметров фильтр обрабатывает в большей степени. Ковариационная матрица ошибок 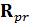 описана следующим образом:
описана следующим образом:
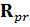 =
= 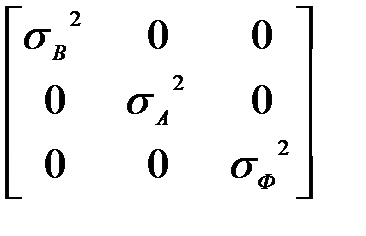 , (6)
, (6)
где 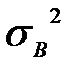
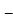 дисперсия оценки компоненты фона,
дисперсия оценки компоненты фона, 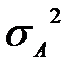 – дисперсия оценки компоненты амплитуды,
– дисперсия оценки компоненты амплитуды, 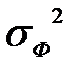 – дисперсия оценки компоненты фазы. Ковариационная матрица шума наблюдения
– дисперсия оценки компоненты фазы. Ковариационная матрица шума наблюдения 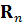 представлена в виде матрицы единичной размерности.
представлена в виде матрицы единичной размерности.
Исходя из своего предназначения, данные параметры могут быть интерпретированы как настройки фильтра. Необходимо подобрать корректные значения для ковариационных матриц, чтобы получить наиболее точные оценки каждой из компонент вектора параметров. Опытным путём были подобраны следующие значения для 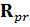 и
и 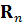 :
:
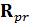 =
= 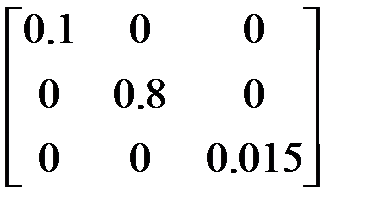 ,
,
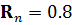 .
.
Одним из критериев подбора значений для ковариационных матриц является то, что евклидовых норм (норм Фробениуса) должны примерно совпадать. При расчёте значение нормы для 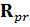 составило 0.8079, для
составило 0.8079, для 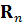 = 0.8. Применив данные настройки к алгоритму фильтра Калмана, были получены следующие результаты, график которых представлен на рис. 4. Был смоделирован сигнал, априорное значение τ для которого равно 7. Красным цветом обозначен исходный сигнал, синим - значения оценки каждой компоненты.
= 0.8. Применив данные настройки к алгоритму фильтра Калмана, были получены следующие результаты, график которых представлен на рис. 4. Был смоделирован сигнал, априорное значение τ для которого равно 7. Красным цветом обозначен исходный сигнал, синим - значения оценки каждой компоненты.
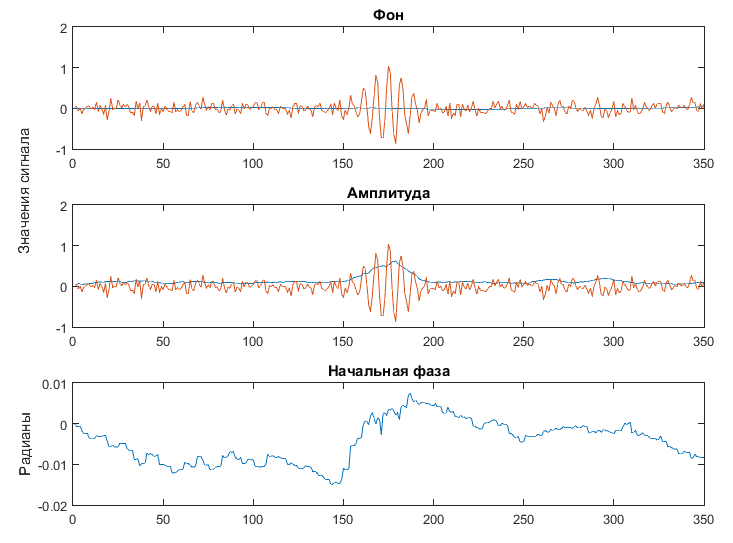
Рис. 4. График результатов работы фильтра Калмана при подобранных настройках фильтра
При рассмотрении рисунка 4 видно, что при подобранных настройках фильтр показал удовлетворительные результаты: оценки фона и амплитуды визуально близки к истинным значениям фона и амплитуды, а значения оценки фазовой компоненты должны находиться в диапазоне от -2π до 2 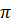 : в данном случае они находятся в диапазоне приблизительно от -0.02 до 0.02.
: в данном случае они находятся в диапазоне приблизительно от -0.02 до 0.02.
Для выполнения основной задачи данной работы, заключающейся в проверке работоспособности фильтра при различных значениях количества отсчетов на период сигнала, удовлетворяющих и не удовлетворяющих критерию Найквиста, в вектор параметров 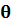 необходимо ввести четвёртую компоненту для оценки параметра сигнала τ. В таком случае вектор параметров будет представлен в следующем виде:
необходимо ввести четвёртую компоненту для оценки параметра сигнала τ. В таком случае вектор параметров будет представлен в следующем виде:
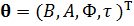 . (7)
. (7)
При этом, определённые компоненты алгоритма должны быть расширены путём добавления нового параметра τ: ковариационная матрица шума ошибок теперь содержит дисперсию оценки компоненты количества отсчетов на период и приобретает следующий вид:
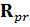 =
= 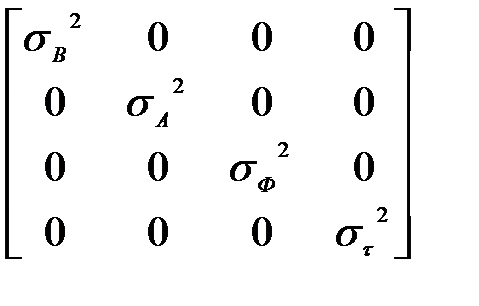 . (8)
. (8)
Также в матрицу H, определённую в уравнении (4), добавляется производная исходного сигнала по четвёртому параметру:
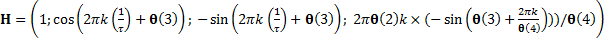 . (9)
. (9)
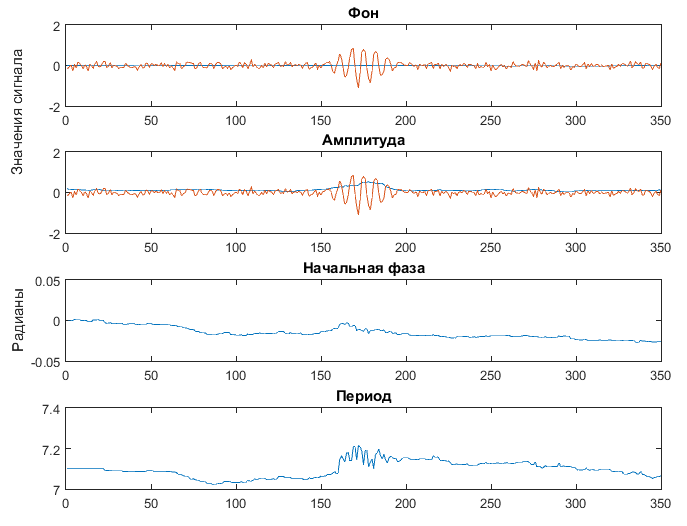
Рис. 5. График результатов работы фильтра Калмана после введения нового оцениваемого параметра
Визуально по представленному на рис. 5 графику также можно сделать вывод, что при текущих настройках фильтр успешно справляется со своей задачей. Нижний график оценки компоненты периода показывает, что значения оценки периода имеют погрешность не более 0.2 относительно истинного значения периода. Также наибольшие отклонения находятся примерно со 150-ого по 200-ый отсчёт - там, где находится информативная часть сигнала.
Далее был смоделирован сигнал, не удовлетворяющий критерию Найквиста. Количество отсчётов на период сигнала равно 1.8. Алгоритм был запущен, с использованием аналогичных настроек.

Рис. 6. Результаты работы фильтра Калмана для сигнала, не удовлетворяющего критерию Найквиста
Как видно, текущие настройки фильтра оказались приемлемыми также для сигнала, у которого количество отсчётов на период меньше двух. В первой главе было сделано наблюдение, что для данной модели интерферометрического сигнала уменьшение количества отсчётов на период до несоблюдения критерия Найквиста приводит к тому, что сигнал начинает содержать в себе кратную частоту, что в итоге не влияет в целом на результаты работы фильтра.
Выводы по главе 2
Была рассмотрена модель расширенного фильтра Калмана, в частности, все его основные параметры и то, как происходит прогнозирование компонент интерферометрического сигнала путём расчёта основных параметров фильтра. Определено, какие параметры алгоритма отвечают за настройки фильтра, вследствие чего опытным путём были подобраны корректные значения для данных параметров. Далее параметры алгоритма были расширены путём добавления компоненты, определяющей количество отсчётов на период сигнала, так как при моделировании сигналов с различной частотой оценка данного параметра должна рассчитываться фильтром. Были смоделированы сигналы с различной частотой, удовлетворяющие критерию Найквиста и не удовлетворяющие ему, для которых был запущен реализованный алгоритм фильтра Калмана. Визуально результаты работы алгоритма указывают на то, что подобранные настройки фильтра корректны для сигналов с различной частотой. Также можно сделать вывод о том, что сигнал с количеством отсчётов на период меньше двух, преобразующийся к кратной частоте, не влияет на результаты работы фильтра.