Отчет по курсовой работе
Тема:
Исследование расширенного фильтра Калмана в задаче обработки квазигармонических сигналов с малым количеством отсчётов
Студент Бухтияров Н.В. Группа B3416
(подпись) (Ф.И.О)
Руководитель Волынский М.А., главный научный сотрудник, к.т.н.
(Ф.И.О., должность, уч. степень)
(подпись) (дата)
Работа защищена ""2020 г. с оценкой
(подпись)
Санкт-Петербург
2020 г.
Министерство науки и высшего образования Российской Федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
“НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
УНИВЕРСИТЕТ ИТМО”
Группа: B3416УТВЕРЖДАЮ
Руководитель ОП_______И.П. Гуров
“____”____________________2020 г.
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Студенту Бухтиярову Никите Владимировичу
Научный руководитель: Волынский М.А., Университет ИТМО, главный
(Фамилия И.О., место работы, должность)
научный сотрудник
1. Тема работы: Исследование расширенного фильтра Калмана в задаче обработки квазигармонических сигналов с малым количеством отсчётов
2. Срок сдачи студентом законченной работы: 17.03.2020
3. Содержание работы:
1) Обзор метода расширенной калмановской фильтрации для интерферометрических сигналов
2) Моделирование интерферометрических сигналов с различным количеством отсчётов на периоде
3) Реализация метода расширенной калмановской фильтрации для смоделированных сигналов
4) Исследование погрешностей результатов работы реализованного алгоритма
4. Исходные данные:
Нет.
5. Содержание отчёта:
1) Описание модели интерферометрического сигнала в системе оптической когерентной томографии
2) Описание алгоритма расширенного фильтра Калмана применительно к интерферометрическим сигналам малой когерентности
3) Моделирование сигналов с изменением количества отсчётов на периоде сигнала, а также их сравнение
4) Описание работы алгоритма расширенного фильтра Калмана применительно к смоделированным сигналам
5) Исследование погрешностей результатов работы алгоритма и определение границ его применимости
6. Перечень графических материалов:
1) Примеры смоделированных сигналов малой когерентности
2) Графики полученных результатов работы фильтра Калмана для смоделированных сигналов
3) Графики рассчитанных погрешностей результатов работы алгоритма
7. Исходные библиографические источники:
1) R. E. Kalman. A New Approach to Linear Filtering and Prediction Problems. // Transactions of the ASME–Journal of Basic Engineering, 82 (Series D). 1960. P. 35-45.
2) S. Huang and G. Dissanayake, Convergence and consistency analysis for Extended
Kalman Filter based SLAM. IEEE Transactions on Robotics, 23(5):1036-1049, 2007
8. Основные этапы и сроки их выполнения:
| № п.п. | Наименование этапов работы | Срок выполнения этапов работы | |
| 1. | Обзор научно-технической литературы по тематике работы | 17.01.2020 | |
| 2. | Описание модели интерферометрического сигнала | 17.01.2020 | |
| 3. | Реализация алгоритма расширенного фильтра Калмана для модели сигнала | 24.01.2020 | |
| 4. | Расчёт погрешностей полученных результатов работы алгоритма | 15.02.2020 | |
| 5. | Анализ результатов работы алгоритма и оформление отчета |
9. Дата выдачи задания: 09.01.2020
Руководитель
(подпись)
Задание принял к исполнению
(подпись)
Оглавление
Введение.................................................................................................................... 4
Глава 1. Модель интерферометрического сигнала малой когерентности............. 6
Глава 2. Реализация алгоритма расширенного фильтра Калмана........................ 9
Глава 3. Расчёт погрешностей для результатов работы реализованного алгоритма................................................................................................................................. 15
Заключение.............................................................................................................. 18
Список литературы................................................................................................. 19
Приложение А. Листинг программы..................................................................... 20
Введение
В интерферометрах белого света, используемых для исследования микрорельефа поверхности объектов с помощью метода оптической когерентной томографии (ОКТ), предпочтительна обработка данных в режиме реального времени [1]. Интерферометр является основной частью системы ОКТ, при этом система обработки поступающих во время выполнения исследования структуры объекта данных рассматриваются как единая система. Основные требования, предъявляемые к обработке данных в этой системе, можно сформулировать следующим образом: разрешающая способность, быстродействие, устойчивость [2]. В силу того, что данные для результата накапливаются по мере сканирования структуры обрабатываемого объекта по глубине, обосновано применение рекуррентных алгоритмов динамического оценивания параметров системы обработки поступающих данных, соответствующих критерию быстродействия. Одним из известных видов алгоритмов динамического оценивания параметров сигналов малой когерентности является фильтр Калмана. Фильтр Калмана представляет собой математический аппарат, позволяющий проводить фильтрацию данных, поступающих в реальном времени, не накапливая их для анализа. Другим известным видом алгоритмов обработки сигналов малой когерентности являются алгоритмы, основанные на преобразовании Фурье, но их применение в системах, работающих в реальном времени, нецелесообразно, так как такие алгоритмы требуют полной информации об обрабатываемом сигнале [3]. Также основанные на преобразовании Фурье методы не всегда устойчивы к шумам, а их разрешающая способность сопоставима с классическими ограничениями, накладываемыми критерием Рэлея [4]. Для увеличения быстродействия алгоритма может быть применено прореживание обрабатываемого интерферометрического сигнала – уменьшение количества отсчётов на период сигнала вплоть до того момента, когда перестанет соблюдаться критерий Найквиста.
Целью работы является исследование свойств алгоритма калмановской фильтрации при различном количестве отсчётов на периоде интерферометрического сигнала и определение границ применимости указанного алгоритма.
Для достижения поставленной цели необходимо решить следующие задачи:
1) Описать модель интерферометрического сигнала малой когерентности
2) Cмоделировать сигналы с различным количеством отсчётов на периоде
3) Сравнить сигналы, характеристики которых соответствуют критерию Найквиста и не соответствуют ему
4) Реализовать алгоритм расширенного фильтра Калмана для смоделированных сигналов
5) Оценить полученные результаты работы фильтра путём расчёта погрешностей
6) Проанализировать полученные результаты
Глава 1. Модель интерферометрического сигнала малой когерентности
Интерферометрический сигнал, получаемый в результате видеосъёмки физического объекта в системе ОКТ, представлен в виде априорной модели вида:
, (1)
где 
– фоновая составляющая, 
– амплитуда, 
– шум с нормальным распределением и нулевым средним, 
– фазовая компонента сигнала, 
– количество отсчётов на один период сигнала. Данная модель представляет собой интерпретацию модели нормального распределения. В данной работе наибольший интерес представляет параметр , так как его изменение влияет на соответствие модели сигнала критерию Найквиста. По описанной модели был построен сигнал, количество отсчётов на период которого равно пяти ( = 5) (рис. 1).
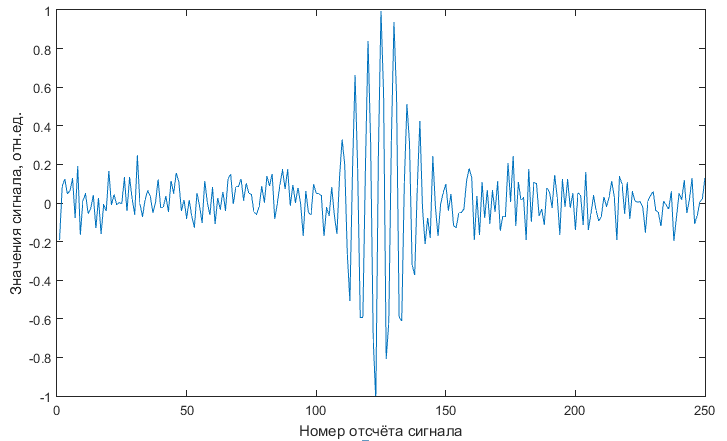
Рис. 1. График смоделированного сигнала (τ = 5)
По представленному графику визуально можно сделать вывод о том, что информативная часть сигнала содержится приблизительно с 100-ого по 150-ый отсчёт. При изменении значения количества отсчётов на период сигнала, при котором соответственно изменялось суммарное количество отсчётов в сигнале, диапазон значений, содержащих информативную часть, не изменялся и составлял порядка 50-ти отсчётов. Моделирование сигналов проводилось таким образом, что суммарное количество периодов косинусоиды, содержащейся в уравнении (1), равно 50, при этом данное значение оставалось неизменным при изменении значения параметра τ.
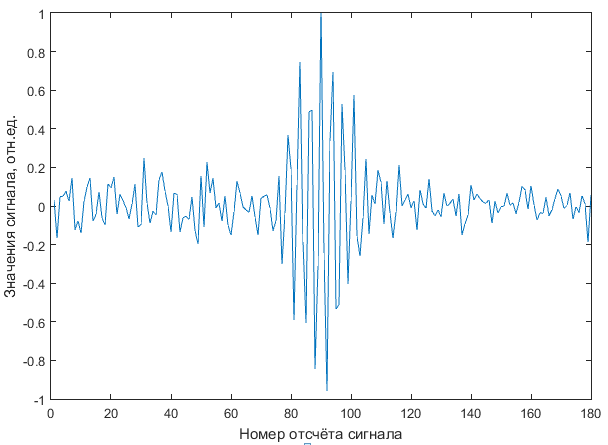
Был смоделирован сигнал, значение τ для которого не соответствовало критерию Найквиста. В интерферометрических сигналах, полученных в системе ОКТ, минимально возможное значение количества отсчётов на период, равно 1.8 (τ < 2). График данного сигнала представлен на рис. 2.
Рис. 2. График смоделированного сигнала (τ = 1.8)
По представленному на рис. 2 графику видно, что при несоответствующей критерию Найквиста частоте данная модель сигнала преобразуется к кратной частоте – количество отсчётов на период удваивается, и в этом случае оно становится равно 3.6. Для более наглядного представления был смоделирован сигнал с априорно заданным параметром τ = 3.6 и проведено сравнение с сигналом, представленном на рис. 2.
(а) (б)
Рис. 3. Сравнение графиков сигналов с параметром τ =1.8 (а) и τ =3.6 (б)
При сравнении данных графиков на рис. 3 можно более наглядно сделать вывод о том, что при уменьшении частоты до несоблюдения критерия Найквиста модель сигнала начинает содержать в себе кратную частоту. Данное наблюдение также будет рассмотрено в главе 2 при описании работы расширенного фильтра Калмана для данных сигналов, так как оно отражается на результатах работы фильтра непосредственно для этих сигналов.
Выводы по главе 1
При моделировании и сравнении двух сигналов, для которых данный параметр соответствует критерию Найквиста и не соответствует ему, выяснилось, что при описанной модели сигнал априорно не будет содержать количество отсчётов на период меньше, чем два, при этом он начнёт выходить на кратную частоту - это означает, что фактическое количество отсчётов на период будет в 2 раза больше.