Для определения качества работы фильтра были проведены эксперименты, заключающиеся в том, что был проведён расчёт погрешностей для оценки каждой компоненты фильтра для разных значений параметра τ, изменяющихся в диапазоне от 1.8 до 21.5 с шагом от 0.1 до 0.5. Для достоверности эксперимента сигнал был смоделирован 50 раз для каждого значения параметра τ, так как сигнал имеет стохастическую природу происхождения. Значение 50 выбрано исходя из критерия P-значения, определяющего достоверность статистических данных, его значение составило 0.0447. Погрешности каждой компоненты были рассчитаны в виде дисперсии, при этом они рассчитывались для диапазона сигнала, содержащего его информативную часть, чтобы уменьшить количество выбросов.

Рис. 7. График погрешностей оценки компоненты фона сигнала при изменении параметра τ

Рис. 8. График погрешностей оценки компоненты амплитуды сигнала при изменении параметра τ

Рис. 9. График погрешностей оценки компоненты фазы сигнала при изменении параметра τ
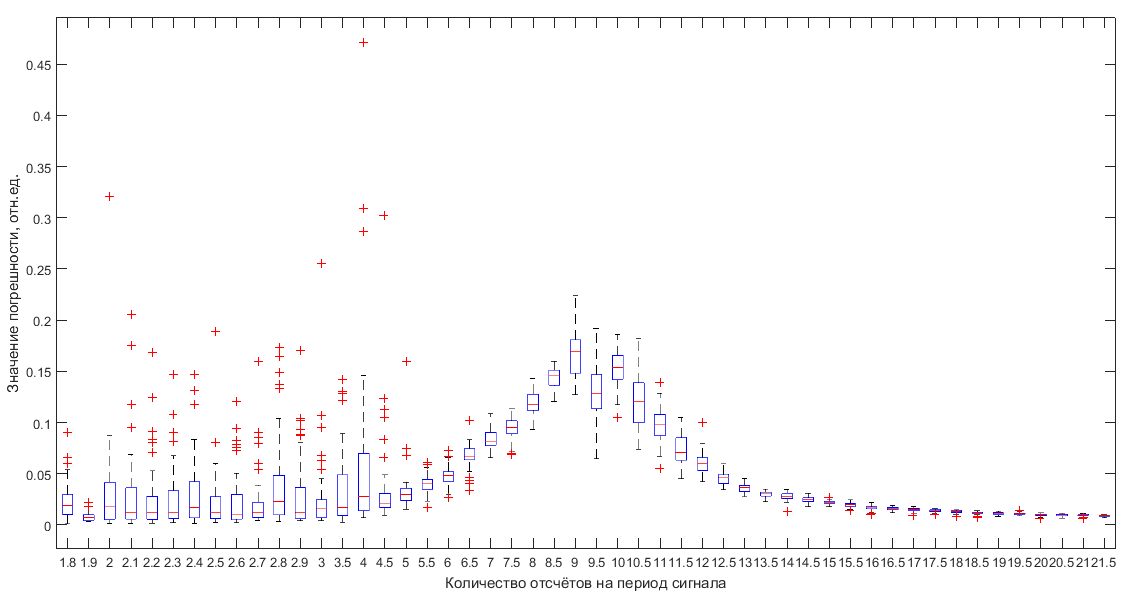
Рис. 10. График погрешностей оценки компоненты количества отсчётов на период сигнала при изменении параметра τ
По данным графикам можно сформулировать следующие наблюдения: погрешности оценок компоненты фона (рис. 7) практически не меняются с увеличением частоты сигнала, но, начиная от τ=10, они постепенно становятся меньше, а значительные выбросы в статистике исчезают после τ = 4.5. При рассмотрении графика погрешностей оценок амплитуды (рис. 8) и частоты (рис. 10) можно заметить, что значительные выбросы также исчезают после τ=4.5 (как на рис. 7), но при этом значения погрешностей начинают волнообразно расти и снижаться примерно в середине графика. График погрешностей оценок компоненты фазы показывает, что значения также волнообразно увеличиваются, и визуально разброс ошибки значительно выше, чем на рис. 7 и рис. 8, но по факту все значения лежат в диапазоне 1% погрешности.
Выводы по главе 3
Полученные зависимости ошибок оценки параметров сигнала от количества отсчетов на периоде показали, что ошибка оценки фоновой составляющей не зависит от соблюдения критерия Найквиста, а остальные параметры корректно оцениваются для всех значений периода сигнала из исследуемого диапазона, однако погрешность уменьшается по мере увеличения количества отсчётов на периоде и становится незначительной (не превышает 1% для каждого параметра) при 5 и более отсчетах на периоде сигнала.
Заключение
Был разработан, исследован и программно реализован алгоритм метода калмановской фильтрации для прогнозирования компонент интерферометрического сигнала малой когерентности, полученного в системе ОКТ. Была произведена настройка точности фильтра путём подбора различных значений ковариационной матрицы ошибки и ковариационной матрицы шума системы. Для смоделированных сигналов с изменяемым количеством отсчётов на период реализованный алгоритм показал приемлемые результаты, при этом настройки точности фильтра не изменились при расширении параметров фильтра после добавления новой фильтруемой компоненты, определяющей количество отсчётов на период сигнала. При расчёте погрешностей для смоделированных сигналов было выявлено, что полученные результаты позволяют сформировать рекомендации к эффективному применению калмановской фильтрации для обработки интерферометрических сигналов малой когерентности. Данный алгоритм позволяет получить удовлетворительные результаты при анализе сигналов с количеством отсчётов на периоде, соответствующим критерию Найквиста, при этом сигнал может иметь небольшое количество отсчетов на периоде (несколько единиц), а существенное увеличение количества отсчетов не приводит к повышению точности оценивания.
Список литературы
1. М.А. Волынский, И.П. Гуров, П.А. Ермолаев, П.С. Скаков. Динамическое оценивание параметров интерферометрических сигналов на основе последовательного метода Монте-Карло. // Научно-технический вестник информационных технологий, механики и оптики. 2014, № 3 (91). С. 18 – 22.
2. М.А.Волынский. Рекуррентные алгоритмы обработки данных в оптической когерентной томографии:. дис. … канд. техн. наук: 05.13.01: защищена 20.12.11, Санкт-Петербург, 2011 – 112 с.
3. М.А. Волынский, А.С. Захаров, И.П. Гуров. Анализ интерференционных сигналов малой когерентности на основе моделей линейной и нелинейной стохастической фильтрации. // Научно-технический вестник информационных технологий, механики и оптики. 2007, №7 (3). С.4 – 8.
4. Фильтр Калмана [Электронный ресурс]. // Научный блог Павла Малинникова – 2013. – URL: https://malinnikov.ru/filtr-kalmana/ (Дата обращения: 10.06.2019).
5. И.А. Тебякин. Повышение точности позиционирования в сетях Wi-Fi с использованием фильтра Калмана:. маг. дис.: 11.04.02, Санкт-Петербургский политехнический университет Петра Великого, Санкт-Петербург, 2016 – 44 с.
6. М.А. Волынский, И.П. Гуров, П.А. Ермолаев, П.С. Скаков. Анализ вычислительной сложности рекуррентных алгоритмов обработки данных в оптической когерентной томографии. // Научно-технический вестник информационных технологий, механики и оптики. 2014, № 6 (94). С. 37 – 40.
7. Калман Р.Э., Фалб П.Л., Арбиб М.А. Очерки по математической теории систем // М.: Едиториал УРСС, 2004. 400 с.
Приложение А.
Листинг программы для реализации алгоритма расширенного фильтра Калмана
1. clc
2. close all;
3. clear all;
4.
5. T_vec = zeros(1,50);
6. T = 1.8;
7. K = round(T*50);
8.
9. DEV_A = zeros(50, 50);
10. DEV_B = zeros(50, 50);
11. DEV_PHI = zeros(50, 50);
12. DEV_T = zeros(50, 50);
13.
14. for k = 1: K
15. kk(k) = k;
16. end
17.
18. sigmaPsi=0.05;
19. sigmaEtaModel=0.01;
20. kk = zeros(1, K);
21. Rpr = [0.1 0 0 0; 0 0.5 0 0; 0 0 0.015 0; 0 0 0 0.05];
22.
23. Rn = 0.01;
24.
25. for n = 1:50
26.
27.
28. B = zeros(1, K);
29. A = zeros(1, K);
30. y = zeros(1, K);
31. z = zeros(1, K);
32.
33. devA = zeros(1,50);
34. devB = zeros(1,50);
35. devPhi = zeros(1,50);
36. devT = zeros(1,50);
37.
38. for i = 1:50
39.
40. for x = 1:K
41. A(x) = exp((-(x-(K/2))^2)/(K/1.5));
42. y(x) =A(x)*cos(2*3.14*(1/T)*x)+normrnd(0,sigmaPsi);
43. z(x)=y(x)+normrnd(0,sigmaEtaModel);
44. end
45.
46. deviationA = zeros(1,K);
47. deviationB = zeros(1,K);
48. deviationPhi = zeros(1,K);
49. deviationT = zeros(1,K);
50.
51. dev_sumA = 0;
52. dev_sumB = 0;
53. dev_sumPhi = 0;
54. dev_sumT = 0;
55.
56.
57. B_est = zeros(1, K);
58. A_est = zeros(1, K);
59. ph_init_est = zeros(1, K);
60. T_est = zeros(1, K);
61.
62. B_est(1) = 0;
63. A_est(1) = 0;
64. ph_init_est(1) = 0;
65. T_est(1) = T + 0.1;
66. Thetta = [B_est(1); A_est(1); ph_init_est(1); T_est(1) ];
67.
68. for k = 1: K
69. H = [1; cos(2*pi*k*(1/Thetta(4))+Thetta(3)); -Thetta(2)*sin(2*pi*k*(1/Thetta(4))+Thetta(3)); (2*pi*Thetta(2)*k*(-sin(Thetta(3) + (2*pi*k)/Thetta(4))))/Thetta(4)^2]';
70. P = Rpr*H'*inv(H*Rpr*H'+Rn);
71. Thetta = Thetta + P * (z(k) - (Thetta(1)+Thetta(2)*cos(2*pi*k*(1/Thetta(4))+Thetta(3))));
72. Thetta(2) = abs(Thetta(2));
73. Thetta(4) = abs(Thetta(4));
74. B_est(k) = Thetta(1);
75. A_est(k) = Thetta(2);
76. ph_init_est(k) = Thetta(3);
77. T_est(k) = Thetta(4);
78. end
79.
80. signal_sub3 = z - B_est;
81.
82. for j = (K/2)- 25:(K/2) + 25
83. deviationA(j) = ((A_est(j) - A(j))^2);
84. end
85.
86. dev_sumA = sum(deviationA)/K;
87. devA(i) = dev_sumA;
88.
89. for j = (K/2)- 25:(K/2) + 25
90. deviationB(j) = ((B_est(j) - B(j))^2);
91. end
92.
93. dev_sumB = sum(deviationB)/K;
94. devB(i) = dev_sumB;
95.
96. devPhi(i) = var(ph_init_est);
97.
98. for j = (K/2)- 25:(K/2) + 25
99. deviationT(j) = ((T_est(j) - T)^2);
100. end
101.
102. dev_sumT = sum(deviationT)/K;
103. devT(i) = dev_sumT;
104.
105. end;
106. T_vec(n)= T;
107.
108. if (T < 3)
109. T = T + 0.1;
110. else
111. T = T + 0.5;
112. end;
113.
114. devA_t = devA';
115. devB_t = devB';
116. devPhi_t = devPhi';
117. devT_t = devT';
118.
119. for f = 1:50
120. DEV_A(f, n) = devA_t(f,:);
121. DEV_B(f, n) = devB_t(f,:);
122. DEV_PHI(f, n) = devPhi_t(f,:);
123. DEV_T(f, n) = devT_t(f,:);
124. end;
125.
126. end;
127. figure(1);
128. boxplot(DEV_A, T_vec), xlabel('Количество отсчётов на период сигнала'), ylabel('Значение погрешности');
129. figure(2);
130. boxplot(DEV_B, T_vec), xlabel('Количество отсчётов на период сигнала'), ylabel('Значение погрешности');
131. figure(3);
132. boxplot(DEV_PHI, T_vec), xlabel('Количество отсчётов на период сигнала'), ylabel('Значение погрешности');
133. figure(4);
134. boxplot(DEV_T, T_vec), xlabel('Количество отсчётов на период сигнала'), ylabel('Значение погрешности');
135. plot(B, k);
136. figure (2),
137. subplot(3,1,1),plot(kk,B_est_sm,kk, z),title('Фон');
138. subplot(3,1,2),plot(kk,A_est_sm, kk,z),title('Амплитуда');
139. subplot(3,1,3),plot(kk,ph_init_est),title('Начальная фаза');