ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ВЕТЕРИНАРНОЙ МЕДИЦИНЫИ БИОТЕХНОЛОГИИ ИМЕНИ К.И. СКРЯБИНА»
Ветеринарно-биологический факультет
Расчетно-графическая работа по математической статистике на тему:
«Статистический анализ вариационных рядов распределения настрига шерсти овец и длины волоса шерсти»
Выполнила
Студентка 1 курса ФВМ 9 группы
Преподаватель:
Москва 2012
Первичные данные.
Таблица 1
| Номер овцы | Настриг шерсти, кг (y) | Длина волоса шерсти, см (x) |
I. Интервальные ряды распределения настрига и длины волоса шерсти.
1. Интервальный рад распределения настрига шерсти.
Минимальное значение – 3,9кг;
Максимальное значение – 5,4кг;
Размах вариации – 1,5кг: r = xmax - xmin;
Число групп вариаций – 6: k = 1 + 3,322 
lg(n);
Длина интервала – 0,25кг: d = r/k.
Таблица 2
| Номер интервала | Группа овец по велечине настрига шерсти | Число овец | Середина интервала | Накопленная частота | |
| нижняя граница | верхняя граница | fi | xi' | fi' | |
| 3,9 | 4,15 | 4,025 | |||
| 4,15 | 4,4 | 4,275 | |||
| 4,4 | 4,65 | 4,525 | |||
| 4,65 | 4,9 | 4,775 | |||
| 4,9 | 5,15 | 5,025 | |||
| 5,15 | 5,4 | 5,275 | |||
| Итого | x | x |
|
|
2. Интервальный ряд распределения по длине волоса шерсти.
Минимальное значение – 12,7см;
Максимальное значение – 24,8см;
Размах вариации – 12,1см: r = xmax - xmin;
Число групп вариаций – 6: k = 1 + 3,322 lg(n);
Длина интервала – 2,02см: d = r/k.
Таблица 3
| Номер интервала | Группа овец по длине волоса | Число овец | Середина интервала | Накопленная частота | |
| нижняя граница | верхняя граница | fi | xi' | fi' | |
| 12,7 | 14,72 | 13,71 | |||
| 14,72 | 16,74 | 15,73 | |||
| 16,74 | 18,76 | 17,75 | |||
| 18,76 | 20,78 | 19,77 | |||
| 20,78 | 22,8 | 21,79 | |||
| 22,8 | 24,82 | 23,81 | |||
| Итого | x | x |
Графическое представление данных.
Рис. 1. Гистограмма интервального ряда распределения по настригу шерсти, кг.
Рис. 2. Полигон интервального ряда распределения по настригу шерсти, кг.
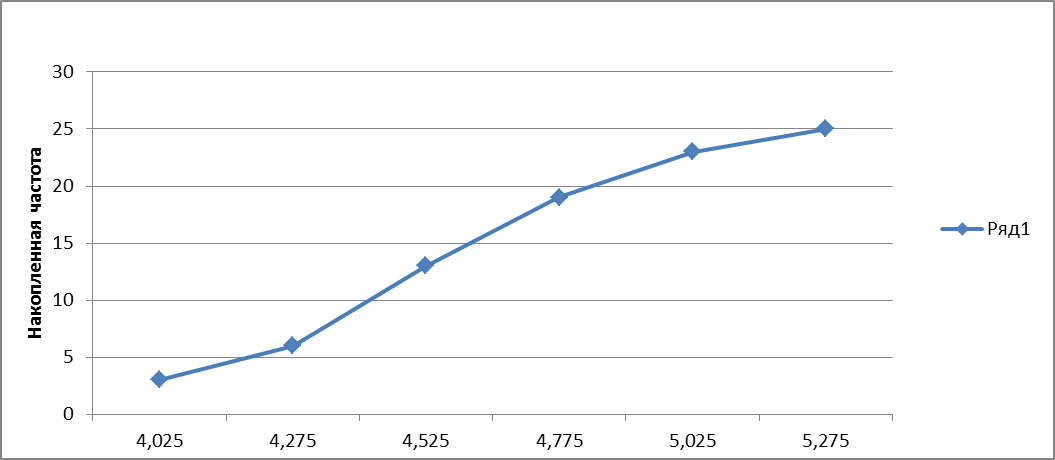
Рис. 3. Кумулята интервального ряда распределения по настригу шерсти, кг.
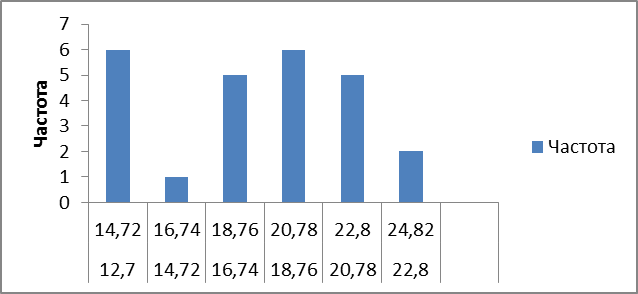
Рис. 4. Гистограмма интервального ряда распределения длины волоса шерсти, см.
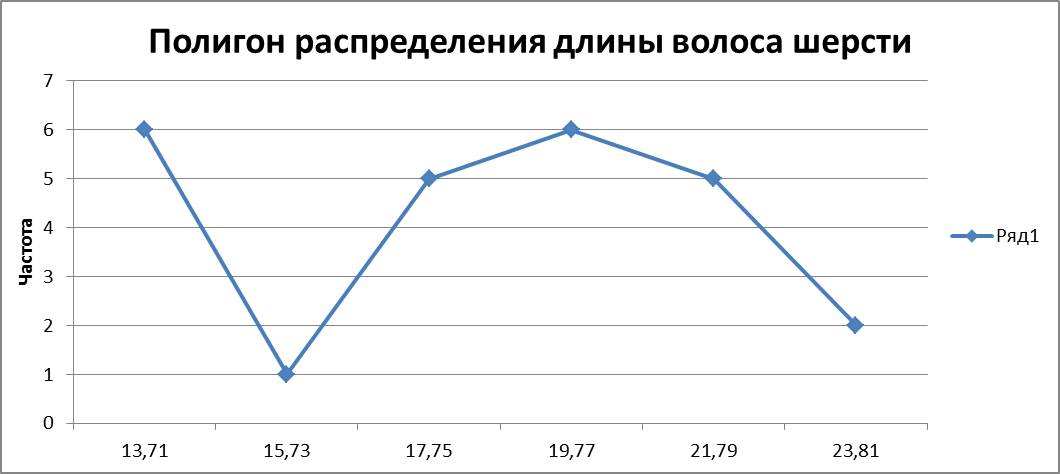
Рис. 5. Полигон интервального ряда распределения длины волоса шерсти, см.
Рис. 6. Кумулята интервального ряда распределения длины волоса шерсти, см.
II. Средние величины. Выборочные показатели вариации и показатели распределения.
Таблица 4
| Показатели | Настриг шерсти | Длина волоса |
| Среднее арифметическое | 4,664 | 18,364 |
| Дисперсия | 0,150733333 | 12,18573333 |
| Среднее квадратичное отклонение | 0,38824391 | 3,490806975 |
| Коэффициент вариации | 8,324269074 | 19,0089685 |
| Асимметрия | -0,298055735 | -0,036048734 |
| Эксцесс | -0,292049096 | -0,923020109 |
| Мода | 4,6 | 13,80181818 |
| Мода (1) | 19,77 | |
| Медиана | 4,63214286 | 18,9283333 |
|
|
III. Ошибки выборочной средней. Доверительный интервал.
1. Абсолютная ошибка выборочной средней
Sx = 
Sx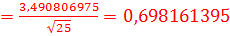 
Sy = 
= 0,0776488
2. Предельная ошибка выборочной средней
ε = t * Sx, где t≈2,1, при P=95%
εx = 2,1* 0,698161395 = 1,466138929
εy = 2,1*0,0776488 = 0,163062442
3. Доверительный интервал для генеральной средней
(
; 
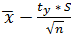Доверительный интервал для генерального среднего настрига шерсти, кг
(4,664 – 0,163062442; 4,664 + 0,163062442)
(4,500937558; 4,827062442)
Доверительный интервал для генеральной средней длины волоса шерсти, см
(18,364 –1,466138929; 18,364 + 1,466138929)
(16,89786107; 19,83013893)
Этот доверительный интервал, который с вероятностью 95% содержит неизвестную длину волоса шерсти всей генеральной совокупности.
IV. Соответствие рядов распределения настрига и длины волоса шерсти нормальному закону распределения.
Проверка гипотез:
Для признака X: признак «длина волоса шерсти» распределен по нормальному закону (α = 0,05).
Дли признака Y: признак «настиг шерсти» распределен по нормальному закону (α = 0,05).
Для проверки гипотез выберем критерий согласия Пирсона – χ2
χ2 = 
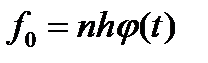Табличное значение для χ2 = 7,815 (для R = 3, α = 0,05)
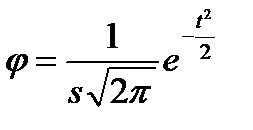
Для признака X:
Таблица 5
| Среднее арифметическое | 18,364 |
| Среднее квадратическое отклонение | 3,490806975 |
| Уровень значимости | 0,05 |
| Степень свободы вариации | |
| Фактический уровень значимости | 0,112686371 |
| Фактическое значение хи квадрат | 8,910532521 |
| Табличное значение хи квадрат | 11,07049775 |
χ2фактическое = 8,91
Вывод: χ2фактическое < χ2теоритическое следовательно нет оснований отвергнуть нулевую гипотезу, т. е. признак «длина волоса шерсти» распределен по нормальному закону (α = 0,05).
|
|
Для признака Y:
Таблица 6
| Среднее арифметическое | 4,664 |
| Среднее квадратическое отклонение | 0,38824391 |
| Уровень значимости | 0,05 |
| Степень свободы вариации | |
| Фактический уровень значимости | 0,916525826 |
| Фактическое значение хи квадрат | 1,469822259 |
| Табличное значение хи квадрат | 11,07049775 |
χ2фактическое = 1,47
Вывод: χ2фактическое < χ2теоритическое следовательно, нет оснований отвергнуть нулевую гипотезу, т. е. признак «настриг шерсти» распределен по нормальному закону (α = 0,05).
Графическое представление данных:
Рис.7 Полигон распределения длины волоса шерсти.
Рис. 8 Полигон распределения настрига шерсти.