Понятие коммутации. Принципы коммутации.

Топографическая диаграмма

Напряжение между отдельными точками трехфазной цепи мож­но найти графически путем построения так называемой топо­графической диаграммы.

Топографическая диаграмма — это векторная диаграмма, по­строенная так, чтобы каждой точке цепи соответствовала опреде­ленная точка на диаграмме и чтобы вектор, проведенный в эту точку из начала координат, выражал по величине и фазе потенци­ал соответствующей точки цепи. Отрезок, соединяющий любые две точки на этой диаграмме, определяет напряжение между соот­ветствующими точками цепи. Если топографическая диаграмма построена в определенном масштабе, то по ней можно опреде­лить искомое напряжение и ток по величине и по фазе.

При построении топографической диаграммы для трехфазной цепи удобно принять за точку с нулевым потенциалом нулевую, или нейтральную, точку генератора. Этой точке генератора соот­ветствует начало координат топографической диаграммы.

Топографическая диаграмма для трехфазной цепи, изображен­ной на рис. 16.6, построена при Условии, что точка 0 на диаграмме (рис. 16.10) соответствует нулевой точке генератора, потенциал ко­торой равен нулю, т. е. φ_О = 0.

Из точки 0 откладываются в определенном масштабе напря­жений Ми векторы фазных ЭДС

Еа, Ев и Ее, в результате чего Получаются точки А, В и С на то­пографической диаграмме. Эти точки на диаграмме соответству­ет началам обмоток генератора, соединенного звездой точками А, В и С цепи.

Отрезок ВС, равный разности векторов Ев - Ее, представляет ^собой линейное напряжение U вс = φ _в-φ_с (падением напряжения на внутреннем сопротивлении обмотки генератора пренебрегаем, т.е. ЕA = Uа). Аналогично отрезки АВ и СА на топографу
ческой диаграмме изображают линейные напряжения Uab и U _сA соответственно.

Отложив из точки 0 (начало координат) вектор напряжения смещения нейтрали Un (отрезок 00'), определяют потенциал ну­левой точки потребителя 0' на диаграмме. Тогда отрезки 0' А, 0', Bи 0'С выражают напряжение на фазах потребителя UA, Uв и U_c.

Если напряжение смещения нейтрали Un отсутствует (Un = 0) то точка 0' (нулевая точка потребителя) на топографической диа­грамме совпадет с точкой 0 (нулевой точкой генератора). Тогда векторы напряжений на фазах потребителя U'_a,U'b и U'_c равны по величине и по фазе векторам ЭДС генератора ЕA, Ев и ЕC.

Применение топографической диаграммы для расчета трехфаз­ной цепи рассмотрено в примере 16.1 настоящей главы.

Пример 16.1

К трехфазной трехпроводной сети с линейным напряжени­ем U_л = 220 В подключен потре­битель, соединенный звездой, с сопротивлениями R_A = R_B = R_C = 10 Ом (рис. 16.11).

Определить напряжение и ток каждой фазы потребителя в каж­дом из трех режимов:

1.Потребители соединены звез­дой, как показано на рис. 16.11.Обрыв в фазе А, т. е. R_A = ∞

2. Короткое замыкание в фазе А, т.е. R_A = 0.

Решение

Решение этой задачи произво­дится с помощью построения то­пографической диаграммы для каждого режима.

1. Так как в данном режиме име­ет место равномерная нагрузка фаз (R_A = R_B = R_c), следовательно, на­пряжение смещения нейтрали UN равно нулю (U_N=0) и точка 0' на топографической диаграмме сов­ падает с точкой 0 (рис. 16.12).

Пренебрегая внутренним сопротивлением обмоток генератора U '_A =Е_А,U'_в =Е_В и Uс = E_с), определяют напряжение на каж­дой фазе потребителя при симметричной системе ЭДС:

 

 

так как Ток каждой фазы потребителя будет равен

Линейные токи в каждом линейном проводе также равны между собой и равны фазным токам каждой фазы, т. е. I_л = I_ф= 12,7 А.

2. При обрыве в фазе А схема трехфазной цепи обретает сле­дующий вид (рис. 16.13а), а топографическая диаграмма показана на рис. 16.136.

Таким образом, точка 0' на топографической диаграмме при об­рыве в фазе А как бы опустилась на вектор линейного напряже­ния Uвс, разделив его величину поровну между U'_B aU'_c, т. е.

 

 

Напряжение на оборванной фазе А, т. е. напряжение между точ­ками 0' и А в схеме, как следует из топографической диаграммы (рис. 16.136),будет равно

 

Токи в фазах: 1_А = 0, так как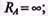

Токи в линейных проводах:

 

3. При коротком замыкании фазы А схема трехфазной цепи по­казана на рис. 16.14а, топографическая диаграмма на рис. 16.146.

Таким образом, точка 0' на топографической диаграмме при коротком замыкании фазы как бы поднялась в точку A (т.е. φо=φA) и фазные напряжения U'_B и U'_c совпали с векто­рами линейных напряжений U_AB и U_AC соответственно и стали равными им по величине, т.е.

U'_в= U_AB =U_л =220В, U'_c = = U_CA=U_л = 220B, a U'_A=0.

 

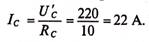Токи в фазах будут равны

 

Ток в коротко замкнутой фазе 1_А, т. е. ток в проводе, соединяю­щем точку 0' и А, определяется геометрической суммой токов I ак =Iв +I_С (рис. 16.146), т.е.

Напряжение U'_B и U'_c и токи I _В и I_с в режимах 2 и 3 легко определить из схем рис. 16.13а и 16.14а, не прибегая к топографи­ческим диаграммам.

56. Понятие о несинусоидальных токах и напряжениях. Принцип Фурье. Гармоники.

57. Расчет несинусоидальной цепи переменного тока.

58. Фильтры.

59. Нелинейные элементы. Статическое и динамическое сопротивления.

60. Цепи с нелинейными активными сопротивлениями.

61. Катушка с ферромагнитным сердечником: магнитный поток, ЭДС, векторная диаграмма.

62. Полная векторная диаграмма и схема замещения катушек с ферромагнитным сердечником.

63. Явление феррорезонанса.

Понятие коммутации. Принципы коммутации.

Переходный процесс в электрической цепи — это электромагнит­ный процесс, возникающий в электрической цепи при переходе от од­ного установившегося (принужденного) режима к другому. Устано­вившимся (принужденным) называется режим работы электриче­ской цепи, при котором напряжение и токи цепи в течение длительного времени остаются неизменными.

Такой режим в электрической цепи устанавливается при длите­льном действии источников постоянной или переменной ЭДС при неизменных параметрах этой цепи R, L и С.

Переходный процесс вызывается коммутацией в цепи.

 

Комму­тацией называется процесс замыкания или размыкания рубильников или выключателей. Переходный процесс может быть вызван изме­нением параметров электрической цепи R, L или С.

Переходный процесс базируется на двух законах коммутации:

1) ток в индуктивности не может изменяться скачком;

2) напряжение на емкости не может изменяться скачком.

Действительно, если ток в индуктивности L изменяется скач­ком, т. е. мгновенно, то ЭДС самоиндукции ei становится беско­нечно большой (при t_KOM = 0):

В реальных цепях ЭДС самоиндукции может иметь только ко­нечные значения.

Если в цепи с емкостью С напряжение на ее обкладках изменя­ется скачком, т. е. мгновенно, то появляется бесконечно большой зарядный (или разрядный) ток (при t_ком = 0):

Ток в электрических цепях может иметь только конечные зна­чения.

Переходный процесс является быстропротекающим процессом, длительность которого обычно составляет десятые, сотые и даже

65. Переходные процессы в RL - цепи при подключении к источнику постоянного тока.

66. Переходные процессы в RC - цепи при подключении к источнику постоянного тока.

67. Переходные процессы в RL - цепи при подключении к источнику переменного тока.

68. Переходные процессы в RC - цепи при подключении к источнику переменного тока.