В качестве форм текущей аттестации используются такие формы, как проверка контрольных работ, решение задач, устные опросы.
Промежуточный контроль имеет форму контрольных работ. Уровень решения задач в них оценивается как уровень овладения обучающимися знаний по данному предмету.
В соответствии с Положением о балльно-рейтинговой системе (БРС) оценки успеваемости студентов во время последней контрольной недели семестра преподаватель подводит итоги работы каждого студента и объявляет результаты студентам.
Однако, если студент желает улучшить свой рейтинг по дисциплине, то ему предоставляется право набрать дополнительные баллы, а именно, пересдать лабораторные работы, решить задачи, выполнить дополнительные задания и т.п.
Поскольку дисциплина преподается в течение одного семестра, для выставления итоговой оценки на зачете выводится средний балл по дисциплине. В случае если средний балл составляет от 40 до 60, студенту предоставляется право сдавать зачет и оценка выставляется непосредственно по его результатам.
Зачет проводится в устно-письменной форме. Он включает письменную часть – решение задач по теме. Устная часть оценивает полученные знания по дисциплине путем собеседования с преподавателем.
Вопросы к экзамену в 1 семестре
1) Матрицы. Понятие матрицы. Линейные операции над матрицами и их свойства
2) Произведение матриц. Свойства произведения матриц.
3) Определители и их свойства. Правило Крамера.
4) Единичная и обратная матрицы. Решение СЛАУ матричным методом.
5) Решение СЛАУ методом Гаусса.
6) Решение СЛАУ методом Гаусса-Жордана.
7) Векторы, действия над ними. Координаты вектора (теорема о базисе плоскости).
8) Скалярное произведение векторов. Свойства и геометрические приложения.
9) Расстояние между точками. Деление отрезка в данном отношении.
10) Векторы в пространстве (теорема о базисе пространства).
11) Векторное произведение векторов. Свойства и геометрические приложения.
12) Смешанное произведение векторов. Свойства и геометрические приложения.
13) Прямая на плоскости. Прямая, проходящая через две точки.
14) Описание прямой, проходящей через заданную точку и с заданным угловым коэффициентом. Условие параллельности и перпендикулярности прямых.
15) Общее уравнение прямой на плоскости. Условие параллельности и перпендикулярности прямых. Уравнение прямой в отрезках.
16) Угол между прямыми. Расстояние от точки до прямой.
17) Плоскость в пространстве. Взаимное расположение плоскостей в пространстве
18) Линии второго порядка на плоскости и их общее описание.
19) Каноническое уравнение эллипса, геометрическая характеристика, построение.
20) Каноническое уравнение гиперболы, геометрическая характеристика, построение.
21) Каноническое уравнение параболы, геометрическая характеристика, построение.
22) Прямые в трехмерном пространстве.
23) Векторное описание плоскости, проходящей через заданную точку перпендикулярно заданному вектору.
24) Векторное описание плоскости, проходящей через три точки.
25) Условия параллельности и перпендикулярности плоскостей.
26) Общее уравнение поверхности. Цилиндрическая поверхность.
27) Эллипсоид, гиперболоид, параболоид, конус
28) Множества и действия над ними.
29) Элементарные функции. Свойства. Графики. Преобразование графиков.
30) Предел функции в точке. Раскрытие неопределенностей.
31) Замечательные пределы.
32) Непрерывность функции в точке.
33) Непрерывность функции на отрезке.
34) Производная функции, её геометрический смысл.
35) Правила дифференцирования. Таблица производных.
36) Основные теоремы дифференциального исчисления (Ферма, Ролля, Лагранжа, Коши).
37) Исследование функции на монотонность и экстремумы.
38) Нахождение направлений выпуклости и точек перегиба графика функции.
39) Правило Лопиталя.
40) Асимптоты графика функции.
41) Формула Тейлора и ее применение.
42) Функция двух переменных, её область определения и график.
43) Частные производные функции двух переменных.
44) Экстремум функции двух переменных: необходимое условие, достаточное условие существования.
45) Условный экстремум. Задача Дидоны. Функция Лагранжа.
46) Глобальный экстремум функции двух переменных в замкнутой области.
47) Неопределённый интеграл и его свойства.
48) Таблица неопределённых интегралов.
49) Метод замены переменной в неопределённом интеграле.
50) Формула интегрирования по частям в неопределённом интеграле.
51) Интегрирование рациональных дробей.
52) Интегрирование некоторых трансцендентных функций.
53) Определённый интеграл и его свойства. Формула Ньютона – Лейбница.
54) Геометрические приложения определённого интеграла.
Вопросы к экзамену во 2 семестре
55) Дифференциальные уравнения первого порядка: интегральная кривая, задача Коши.
56) Дифференциальные уравнения с разделяющимися переменными.
57) Дифференциальные уравнения линейные, однородные относительно переменных.
58) Уравнения Бернулли.
59) Уравнения в полных дифференциалах.
60) Дифференциальные уравнения второго порядка линейные с постоянными коэффициентами.
61) Методы отыскания частных решений дифференциальных уравнений с постоянными коэффициентами.
62) Системы линейных дифференциальных уравнений.
63) Числовые ряды. Сходимость ряда.
64) Бесконечно убывающая геометрическая прогрессия. Признаки сравнения положительных рядов.
65) Признаки сходимости положительных и знакочередующихся рядов. Абсолютная и условная сходимость.
66) Функциональные ряды. Сходимость степенных рядов. Теорема Абеля.
67) Ряды Тейлора. Таблица разложений основных функций в ряд Маклорена.
68) Применение рядов в приближенных вычислениях.
69) Элементы комбинаторики.
70) Определения вероятностей. Алгебра событий.
71) Теоремы сложения и умножения.
72) Полная вероятность. Формула Байеса.
73) Схема Бернулли. Формула Муавра-Лапласа.
74) Случайные величины и их характеристики.
75) Системы случайных величин.
76) Закон больших чисел.
77) Предварительная обработка данных.
78) Статистические оценки.
79) Доверительный интервал.
80) Проверка статистических гипотез. Критерий Пирсона.
81) Корреляция и регрессия.
82) Задачи линейного программирования.
83) Графический метод решения задач ЛП.
84) Симплексный метод решения задач ЛП.
85) Симплексные таблицы.
86) Теория двойственности.
87) Метод искусственного базиса.
88) Транспортная задача в матричной постановке.
89) Транспортная задача в сетевой постановке.
90) Транспортная задача с ограничениями на пропускную способность.
91) Основные понятия теории игр. Матричные игры.
92) Игры в чистых стратегиях.
93) Игры в смешанных стратегиях. Теорема Неймана.
94) Графический метод решения игры с двумя стратегиями.
95) Приведение матричной игры к задаче линейного программирования.
Тесты по математике
1. Вычислить 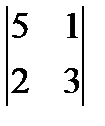
A) 13
b) -13
c) 6
2. Указать точку, через которую проходит прямая 2x+3y=24
a) (9, 1)
b) (-9, 2)
C) (9, 2)
3. Найти длину высоты ВD треугольника с вершинами A(-4, -3), В(0, 2), С(1, -3)
a) 3
b) 2
C) 5
4. Найти объем тетраэдра, ограниченного плоскостью 2x-3y+4z=24 и координатными плоскостями
A) 192
b) 576
c) 24
5. Найти предел функции 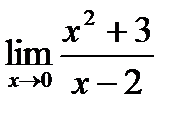
a) 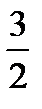
b) 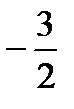
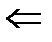
с) 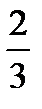
6. Найти производную функции 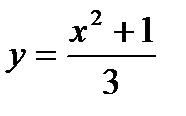
a) 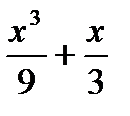
b) 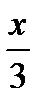
c) 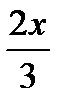
7. Найти первообразную функции 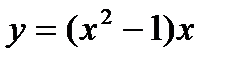
a) 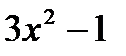
b) 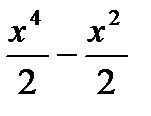
c) 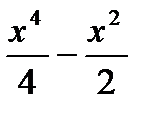
8. Найти уравнение с угловым коэффициентом и смещением, соответствующее уравнению прямой 2x+3y=24
a) 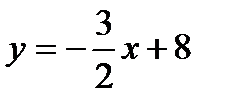
b) 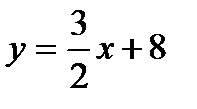
с) 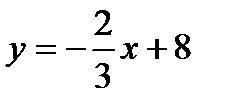
9. Найти угол между прямыми x=0иx=5
a) 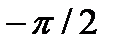
B) 0
c) 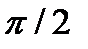
10. Найти угол между прямыми x=2 и y=3
a) 0
b) 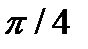
c) 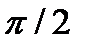
11. Указать пару параллельных прямых
K: y=2x+1 L: 2x+y=3 M: 2x-y=6
a) K, L
b) нет параллельных
С) K, M
12. Указать пару ортогональных прямых
K: y=-x+2 L: 2x+2y=3 M: 3x-3y=5
A) K, M
b) нет ортогональных
с) K, L
13. Указать прямую, параллельную прямой y=-3x+2 и проходящую через точку М(0, -2)
a) y=-2x-3
b) y=-3x-2
c) y=3x-2
14. Указать прямую, перпендикулярную прямой y=-3x+2 и проходящую через точку М(0, -2)
a) y=2x-3
b) 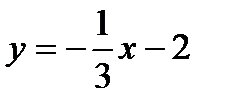
c) 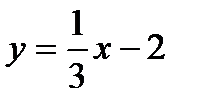
15. Найти длину высоты ВD треугольника с вершинами
A(-4, -3), В(0, 2), С(1, -3)
a) 3
b) 2
C) 5
16. Указать точку, через которую проходит плоскость 2x-3y+4z=24
a) (8, 0, -2)
b) (0, 8, 2)
C) (8, 0, 2)
17. Указать нормальный вектор плоскости 2x-3y+4z=24
a) (2, 3, 4))
B) (2, -3, 4)
c) (-2, 3, 4)
18. Найти расстояние от начала координат до плоскости 2x-3y+4z=24
a) 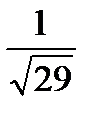
b) 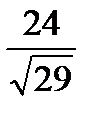
c) 24
19. Найти уравнение в отрезках, соответствующее уравнению плоскости
2x-3y+4z=24
a) 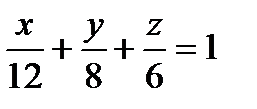
b) 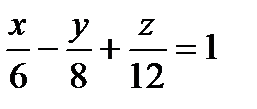
c) 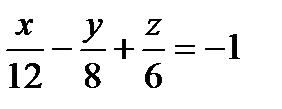
20. Найти объем тетраэдра, ограниченного плоскостью 2x-3y+4z=24 и координатными плоскостями
A) 192
b) 576
c) 24
21. Найти угол между плоскостями x=0 и x=5
a) 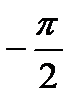
B) 0
c) 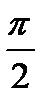
22. Найти угол между плоскостями x=2 и y=3
a) 0
b) 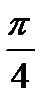
c) 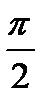
23. Указать пару параллельных плоскостей
K: 2x+y-3z=1 L: x+y-3z=3 M: 4x+2y-6z=5
a) K, L
b) нет параллельных
c) K, M
24. Указать пару ортогональных плоскостей
K: x+y-3z=2 L: 3x+z=3 M: 2x-y=5
a) K, M
b) L, M
c) K, L
25. Указать плоскость, параллельную плоскости 3x+y+5z=2 и проходящую через точку М(0, -1, 1)
a) 3x+y+5z=4
b) 9x+3y-15z=9
c) 3x+3y-15z=-2
26. Указать прямую, перпендикулярную плоскости 3x+2y-z=8 и проходящую через точку М(0,8,6)
a) 9x+3y-15z=-2
b) 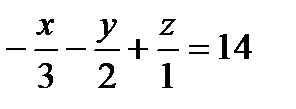
c) 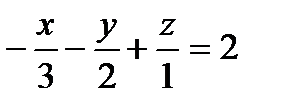
27. Найти длину средней линии MN ║ АВ треугольника ABС с вершинами
A(-6, -3, -2), В(0, 3, 2), С(2, -3, -4)
a) 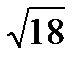
b) 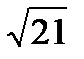
c) 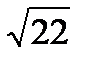
28. Найти уравнение плоскости, проходящей через точки
A(0, -3, -1), В(0, 0, 2), С(2, -3, 0)
a) x+2y+2z+4=0
b) 2x+y+z=0
c) x-y+z+5=0