Новые_значения_X; константа)

Автор: Вардомацкая Елена Юрьевна, ст. преподаватель кафедры математики и информационных технологий УО "Витебский государственный технологический университет".

Известные_значения_Y – это зависимый массив или интервал данных.

Новые_значения_X – массив (или интервал данных), который должен содержать столбец (или строку) для каждой независимой переменной, как и

Известные_значения_X. Если аргумент новые_значения_X опущен, то предполагается, что он совпадает с аргументом известные_значения_X.

константа – логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.

Пример 1. В таблице 2 приведены показатели уровня жизни по территориям регионов республики Беларусь за 200Хг. Провести анализ зависимости среднедневной заработной платы, руб. (Y) от среднедушевого прожиточного минимума в день одного трудоспособного, руб.().

Таблица 2. – Показатели уровня жизни по территориям регионов республики Беларусь за 200Хг

Разместим таблицу с исходными данными в ячейках А3:С24 рабочего листа Excel. В ячейки В22-В24 внесем значения среднедушевого прожиточного минимума, для которых требуется выполнить прогноз уровня среднедневной заработной платы (см рис.1).

Чтобы выполнить анализ зависимости среднедневной заработной платы, руб. (Y) от среднедушевого прожиточного минимума в день одного трудоспособного, руб. (X) следует построить однофакторную регрессионную модель вида y = m∙x + b

Рассчитаем линейную регрессионную однофакторную модель (см. рис.1 и рис.2), для чего в ячейки Е5:А9 введем функцию ЛИНЕЙН в формате: =ЛИНЕЙН(C6:C21;B6:B21;1;1).

Результатом работы функции является массив значений:

ячейки E5, F5 – коэффициенты уравнения регрессии m=1.4111 и b=3816,154;

ячейка Е7 – коэффициент детерминированности R² =0.885;

ячейка E8 – критерий Фишера F=108.12.

Рис.1 – Расчет однофакторной регрессионной модели. Результаты

Таким образом однофакторная регрессионная модель, оценивающая влияние среднедушевого прожиточного минимума в день одного трудоспособного на величину среднедневной заработной платы имеет вид:

Y = 1.411∙x + 3816.154

Вывод: поскольку коэффициент детерминированности R²=0.885 лежит в пределах 0,75 – 1, расчетное значение критерия Фишера F=108,12 больше табличного (FРАСПОБР(0,05;1;F8)= 4,6), модель следует признать адекватной, и использовать для прогнозирования.

В ячейке С22 рассчитаем прогнозное значение среднедневной заработной платы по формуле =E5*B22+F5. В ячейках С23, С24 расчет аналогичен (см. рис.2).

В ячейках Е12:Е14 рассчитаем прогнозное значение среднедневной заработной платы для среднедушевого прожиточного минимума, равного 4000 руб., 4500 руб., 5000 руб. (ячейки В22–В24) с использованием функции ТЕНДЕНЦИЯ:

=ТЕНДЕНЦИЯ(C6:C21;B6:B21;B22:В24;1)

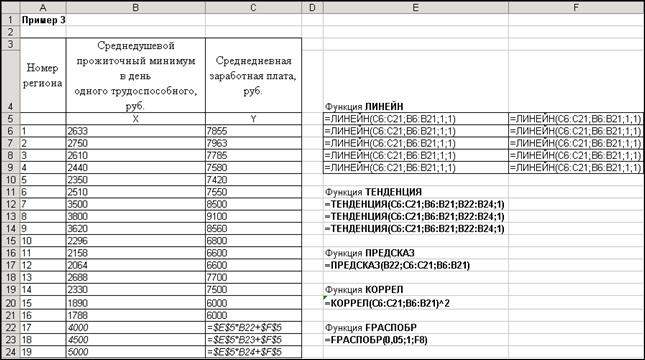
Рис. 2 – Расчет однофакторной регрессионной модели. Формулы

В ячейке Е15 рассчитаем прогнозное значение среднедневной заработной платы с использованием функции ПРЕДСКАЗ:

=ПРЕДСКАЗ(B22;C6:C21;B6:B21).

В ячейке Е18 рассчитаем значение коэффициента корреляции R²:

=КОРРЕЛ(C6:C21;B6:B21)^2.

В ячейке Е12 рассчитаем табличное значение критерия Фишера:

=FРАСПОБР(0,05;1;F8)

Полученные значения совпали c результатами, возвращенными функцией ЛИНЕЙН.

Для построения моделей на основании экспоненциальной зависимости и дальнейшего расчета прогнозов Excel предлагает функции ЛГРФПРИБЛ и РОСТ, работа которых основана на вычислении экспоненциальной кривой, аппроксимирующей данные. Эти функции могут использоваться как для расчета однофакторных, так и многофакторных моделей.

Функция ЛГРФПРИБЛ в регрессионном анализе вычисляет экспоненциальную кривую, аппроксимирующую данные, и возвращает массив значений, описывающий эту кривую. Она является универсальной для расчета параметров экспоненциальных моделей, так как кроме коэффициентов уравнения регрессии может возвращать и дополнительную статистику по регрессии.

Формат