Автор: Вардомацкая Елена Юрьевна, ст. преподаватель кафедры математики и информационных технологий УО "Витебский государственный технологический университет".
План лекции
· Построение корреляционно-регрессионных моделей в СКМ Maple
· Поиск оптимальных решений в СКМ Maple
Построение корреляционно-регрессионных моделей в СКМ Maple
При использовании системы символьной математики Maple для построения экономико-математической модели выбор вида модели не предопределен разработчиками пакета. СКМ Maple позволяет пользователю произвольно, по своему усмотрению, задавать вид модели и при необходимости оперативно его изменять.
Построить и оценить регрессионную модель в СКМ MAPLE можно с помощью модулей и функций статистической библиотеки stats(таблица 1).
Подключение этой библиотеки осуществляется командой
>with(stats);
Таблица 1. Подбиблиотеки библиотеки stats
| Подбиблиотеки | Описание |
| importdata | импорт данных из файла |
| anova | вариационный анализ |
| describe | cтатистические характеристики |
| fit | аппроксимация данных |
| random | cлучайные значения |
| statevalf | численная оценка данных |
| statplots | графика |
| transform | преобразования данных |
Подбиблиотека Fit
Эта подбиблиотека предназначена для нахождения корреляционных отношений и для аппроксимации данных выбранными зависимостями с использованием метода наименьших квадратов.
Формат:
fit[leastsquare[[x,y]]]([[dataX], [dataY]]);
По умолчанию система приближает зависимость к уравнению прямой линии.
Пример 1. Провести анализ зависимости среднедневной заработной платы, руб. (Y) от среднедушевого прожиточного минимума в день одного трудоспособного, руб. (х). Таблица П1 с исходными данными приведена в Приложении 1 к лабораторной работе №8.
Сеанс работы в Maple:
На первом этапе массивы данных x – среднедушевой прожиточный минимум в день одного трудоспособного и Y – среднедневная заработная плата следует оформить типом statsdata для возможности обработки процедурами и функциями библиотеки stats СКМ Maple:
> restart;
> with(stats);
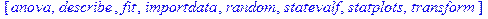
>X:=[1788,1890,2064,2158,2296,2330,2350,2440,2510,2610,2633,2688,2750,3500,3620,3800];
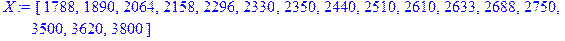
>Y:=[6000,6000,6600,6600,6800,7500,7420,7580,7550,7785,7855,7700,7963,8500,8560,9100];
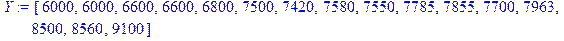
Для расчета функциональной зависимости между экспериментальными данными X и Y и возможности ее графического отображения определим функцию пользователя spisok=f(x) c использованием функционального оператора à:
> spisok:=(x,y)->[x,y];
Далее, задав вид модели (например, линейная), рассчитаем коэффициенты уравнения регрессии:
> fit[leastsquare[[x, y]]]([X,Y]);
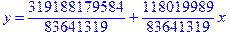
и приведем полученное уравнение к численному виду:
> f:=evalf(%,4);
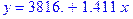
Следует отметить, что при определенной ранее функциональной зависимости между независимой и зависимой переменными функция leastsquare[[x,y],y=f(x)] позволяет задавать вид модели по усмотрению разработчика. Если задать, например, квадратичную или кубическую зависимость, можно рассчитать и такие модели:
> eq:=y=z*x^2+b*x+c;
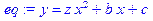
> evalf(fit[leastsquare[[x, y], eq]]([X,Y]),4);
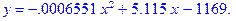
>evalf(fit[leastsquare[[x,y],y=a*x^3+b*x^2+c*x+d]]([X,Y]),7);
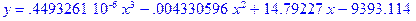
Для вычисления описательных характеристик, используемых при анализе статистических данных, можно использовать функцию describe.
Подробнее с этой темой можно ознакомиться в [8, 9].