Автор: Вардомацкая Елена Юрьевна, ст. преподаватель кафедры математики и информационных технологий УО "Витебский государственный технологический университет".
Это так называемая утилита “Поиск решения” (см. рис. 1). Прокомментируем некоторые аспекты работы с этой утилитой.
Рис.1– Окно утилиты Поиск решения
Искомые переменные - ячейки рабочего листа Excel - называются регулируемыми ячейками.
Целевая функция F(x1, x2, …, xn), называемая иногда просто целью, должна задаваться в виде формулы в ячейке рабочего листа. Эта формула может содержать функции, определенные пользователем, и должна зависеть (ссылаться) от регулируемых ячеек. В момент постановки задачи определяется, что делать с целевой функцией. Возможен выбор одного из вариантов:
Ø найти максимум целевой функции F(x1, x2, …, xn);
Ø найти минимум целевой функции F(x1, x2, …, xn);
Ø добиться того, чтобы целевая функция F(x1, x2, …, xn) имела фиксированное значение: F(x1, x2, …, xn) = a (см. рис. 2).
Рис.2 – Определение целевой функции в окне утилиты «Поиск решения»
Функции G(x1, x2, …, xn) называются ограничениями. Их можно задать как в виде равенств, так и неравенств.
На регулируемые ячейки (искомые параметры – x1, x2, …, xn) можно наложить дополнительные ограничения: неотрицательности и/или целочисленности, тогда решение ищется в области положительных и/или целых чисел (см. рис.3).
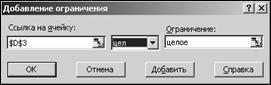
Рис. 3 – Определение ограничений
Под эту постановку попадает самый широкий круг задач оптимизации, в том числе решение различных уравнений и систем уравнений, задачи линейного (см. выше) и нелинейного программирования.
Пример. Решить линейную оптимизационную задачу.
Фирма производит три вида продукции (A, B, C), для выпуска каждого требуется определенное время обработки на четырех устройствах.
|
|
| Вид продукции | Время обработки, ч. | Прибыль, у.е. | |||
| I | II | III | IV | ||
| A | |||||
| B | |||||
| C |
Максимально допустимое время работы на устройствах I, II, III, IV составляет соответственно 84, 42, 21 и 42 часа.
Требуется рассчитать план производства, обеспечивающий максимальную прибыль.
Решение.
Составим ЭММ задачи.
Разместим таблицу с исходными данными в ячейrах A1:G9 Рабочего листа Excel как показано ниже
и выполним необходимые предварительные расчеты (см. рис.5)
Рис. 5 – Исходные данные оптимизационной задачи
Отыскать решение задачи, приняв следующие условия
| 1. | Общая итоговая прибыль (F6) => max |
| 2. | Количество изделий (G3:G5)- целое и неотрицательное число |
| 3. | Баланс времени по каждому устройству (B7:E7) <= (B9:E9) |
| 4. | Изменению подлежат: количество изделий (G3:G5) |
Окончательный вид формулировки задачи представлен на рис. 6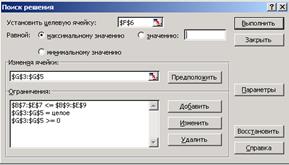 
Рис.6 – Формулировка задачи в терминах рабочего листа Excel
Итоговый результат представлен на рис.7:
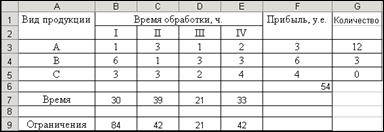Рис.7 – Результат оптимизации
Анализ решения показывает, что все без исключения требования задачи оптимизации выполнены. При этом видно, что для получения максимальной прибыли нецелесообразно выпускать изделие C.
Результаты расчетов представлены в отчете по результатам (рис.8):
Рис. 8 – Отчет по результатам
Утилита «Поиск решения» может использоваться и для решения более сложных задач оптимизации.
|
|
Лекция 8