Удобным способом представления логических выражений являются схемы: переключательные, логические и др.
Задача 1. Составить переключательную схему, соответствующую логическому выражению А × В + С × В.
Переключательная схема включает в себя элементы параллельного и последовательного соединений. Параллельное соединение соответствует операции ИЛИ, а последовательное – операции И.
Задача 2. Составить по данной схеме логическое выражение и упростить его.
 |
 |
Составим логическое выражение: (А + В)×(В + С × А).
Упростим его: (А + В)×(В + С × А) º А × В + А × С × А + В × В + В × С × А º А × В + 0 + + 0 + В × С × А º А × В + В × С × А.
Задача 3. Составить логическое выражение F по данной схеме.
 |
В данной логической схеме логические операции И, ИЛИ, НЕ представлены соответствующими обозначениями. Логическое выражение будет следующим:
F = А × В × (В + С).
Задача 4. Вычислить значение F, если А =истина, В =ложь.
 |
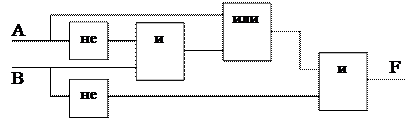Подставим на схеме значения логических переменных А и В, обозначив 1 – истина, 0 – ложь, и вычислим значение F.
Задача 5. Составить логическую схему по данному логическому выражению: F = А + В ×(С + А).
 |
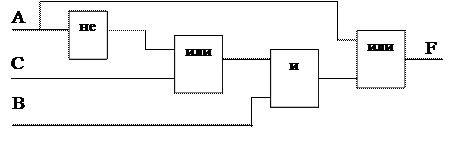Задача 6. По данной комбинационной схеме устройства составить логическое выражение F.
 |
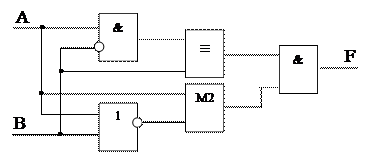В данной схеме использованы следующие обозначения: & – конъюнкция, 1 – дизъюнкция, º – эквивалентность, М2 – сложение по модулю 2, – отрицание.
F = (А × B º B) × (A Å A + B).
Логические задачи
При решении логических задач вначале обозначают простые высказывания как логические переменные латинскими буквами, затем составляют логические выражения и упрощают их с помощью формул преобразования логических выражений (см. выше).
Задача 1. Кто из учеников А, В, С и D играет, а кто не играет в шахматы, если известно следующее:
а) если А или В играет, то С не играет;
б) если В не играет, то играют С и D;
в) С играет.
Решение. Определим следующие простые высказывания:
А – «Ученик А играет в шахматы»;
В – «Ученик В играет в шахматы»;
С – «Ученик С играет в шахматы»;
D – «Ученик D играет в шахматы».
Запишем сложные высказывания, выражающие известные факты:
а) 
;
б) 
;
с) С.
Запишем произведение указанных сложных высказываний:
.
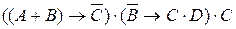Упростим эту формулу:
Ответ. В шахматы играют ученики C и D, а ученики A и B – не играют.
Задача 2. Один из трех братьев поставил на скатерть кляксу. На вопрос “Кто это сделал?” получены такие ответы:
1. Алеша: “Витя не ставил кляксу. Это сделал Боря.”
2. Боря: “Это Витя поставил кляксу. Алеша не пачкал скатерть.”
3. Витя: “Боря не мог этого сделать. Я сегодня не готовил уроки.”
Оказалось, что двое мальчиков в каждом из двух своих заявлений сказали правду, а один оба раза сказал неправду. Кто поставил кляксу?
Введем обозначения:
А – «Алеша поставил кляксу»;
В – «Боря поставил кляксу»;
V – «Витя поставил кляксу».
Запишем теперь суждения мальчиков формулами:
1. V × B.
2. V × A.
По словам Вити, он не делал сегодня уроки, но это не означает, что он не мог поставить кляксу. Поэтому
3. B × (V + V), т.е. В.
По условию задачи, две формулы истинны, а одна ложна. Следовательно, получим
 |  |  |
F =(V × B)×(V × A)× B +(V × B)×(V × A)× B +(V × B)×(V × A)× B.
Преобразуем данное логическое выражение:
 |
F = V×B×V×A×B + V×B×V×A×B + V×B×V×A×B = 0 + 0 + (V +B)×V×A×B =
= (V+B)×V×A×B = V×V×A×B + B×V×A×B = V×A×B + V×A×B = V×A×B.
Таким образом, кляксу поставил Витя.
Лабораторная работа № 3
1. Определить количество строк в таблице истинности для логической функции 
, в которых значение функции F совпадает со значением переменной А.
2. Определить количество нулей в столбце F таблицы истинности для логической функции 
.
3. Определить количество нулей в столбце истинности для логической функции 
.
4. Определить истинность формулы 
.
5. Определить истинность формулы 
.
6. Определить истинность формулы 
.
7. Упростить логическую формулу и определить её истинность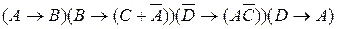 
.
8. Определить значение формулы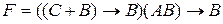 
.
9. Определить значение формулы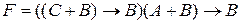 
.
10. Упростить логическое выражение (В º С) ® (В ® А).
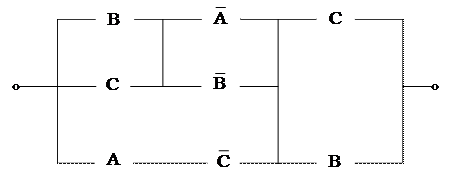
11. Составить по данной схеме логическое выражение и упростить его.
 |
12. Составить по данной схеме логическое выражение и вычислить его значение при А =истина, В =истина, С =ложь.
 |
13. Построить логическую схему по логическому выражению.
F = D ×(A ×(B + C)+ B × C).
14. По данной комбинационной схеме устройства составить логическое выражение F и упростить его.
