ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ КОРРЕЛЯЦИИ
Цель работы: изучить основные приёмы проведения корреляционного и ковариационного анализа с помощью встроенных функций MSExcel и с использованием инструментов Пакета анализа: «Корреляция» и «Ковариация».
Корреляционный анализ представляет собой статистический метод выявления взаимозависимостей между несколькими признаками.
Функциональной зависимостью между случайными величинами X и Y называется зависимость, при которой изменение величины X влечёт изменение значений Y, то есть Y является функцией случайного аргумента X.
Если каждому значению одной переменной соответствует множество возможных значений другой переменной, т.е. каждому значению одной переменной соответствует определённое (условное) распределение другой переменной, то такая зависимость называется статистической (стохастической, вероятностной).
Статистической зависимостью между случайными величинами называется зависимость, при которой изменение одной из величин влечёт изменение распределения другой.
Корреляционной зависимостью между случайными величинами называется статистическая зависимость, при которой изменение одной из величин влечет изменение среднего значения другой.
Вычисление оценок ковариации и выборочных коэффициентов корреляции
Ковариация характеризует рассеивание и взаимную зависимость случайных величин, имеет размерность, равную произведению размерностей случайных величин.
Предположим, что в результате n испытаний система двух случайных величин (X, Y) приняла следующие значения: (x1, y1),(x2, y2),…, (xi, yi), …,(xn, yn). Статистическая оценка ковариации определяется по формуле:
Статистическая оценка ковариации вычисляется по формуле:
 ,
,
где:  и
и  .
.
Для вычисления ковариации в MSExcel используется функция КОВАР(Массив1,Массив2), которая находится в категории Статистические.
Пример 1. Имеется выборка из генеральной совокупности системы двух случайных величин X и Y. Определить ковариацию этих случайных величин.
| xi | 12,1 | 14,7 | 20,5 | 11,2 | 16,6 | 10,0 | 13,0 | 14,9 | 16,3 | 15,1 |
| yi | 53,2 | 44,2 | 51,4 | 57,7 | 45,5 | 42,0 | 53,5 | 68,9 | 57,7 | 63,3 |
Решение
Введём исходные данные в диапазон A1:К12.
В ячейку D3 ввести формулу =КОВАР(B1:K1;B2:K2). Получим результат: 2,709.
Ковариация имеет размерность. Более удобной величиной, характеризующей только зависимость случайных величин, является коэффициент корреляции. Выборочный коэффициент корреляции Пирсона рассчитывается по формуле:
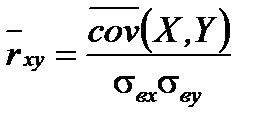 .
.
Для вычисления выборочного коэффициента корреляции Пирсона в MSExcel используется функция КОРРЕЛ(Массив1,Массив2), которая находится в категории Статистические.
Для данных примера 1 рассчитаем коэффициент корреляции.
В ячейки D4 введём формулу =КОРРЕЛ(B1:K1;B2:K2) и получим результат:0,116.
В MSExcel можно вычислить коэффициент детерминации ‒ квадрат коэффициента корреляции Пирсона. Этот коэффициент показывает долю вариации зависимой переменной, учтённой в модели и обусловливаемой вариацией включенных факторов. Для этого используется функция: =КВПИРСОН(Известные_y; Известные_x).
Рассчитаем коэффициент детерминации для данных примера 1. В ячейку D5 введём формулу: =КВПИРСОН(B2:K2;B1:K1). Получим результат: 0,013.

Для проверки значимости выборочного коэффициента корреляции следует проверить нулевую гипотезу H 0: rxy = 0против альтернативной гипотезы H 1: rxy ¹ 0.
Если H 0 принимается, то нет корреляционной зависимости между случайными величинами X и Y. Если H 0отвергается, то существует корреляционная зависимость между случайными величинами X и Y. Для проверки нулевой гипотезы при уровне значимости a необходимо вычислить наблюдаемое значение критерия по формуле:
 .
.
Для уровня значимости a и числа степеней свободы  с использованием распределения Стъюдента найти число
с использованием распределения Стъюдента найти число  .
.
Сравнить числа  и
и  : если
: если  <
<  , то нет основания отвергать гипотезу H 0; если
, то нет основания отвергать гипотезу H 0; если  >
>  , тогипотеза H 0отвергается.
, тогипотеза H 0отвергается.
Проверим значимость выборочного коэффициента корреляции, полученном в примере 2.
В ячейку D6 введём формулу
=D4*КОРЕНЬ(10-2)/КОРЕНЬ(1-CD4^2). Получим результат: 0,33.
В ячейке D7 рассчитаем критическое значение по формуле: =СТЪЮДРАСПОБР(0,05;8). Получим критическое значение для случая двусторонней критической области, равное 2,306. Так как Тнабл. < Ткр., то нулевая гипотеза принимается.
Наряду с выборочным коэффициентом корреляции Пирсона используются также выборочные коэффициенты ранговой корреляции Спирмена и Кендалла. Эти коэффициенты можно применить как к данным, измеренным в количественных шкалах, так и данным, измеренным в порядковой шкале.
Коэффициент ранговой корреляции Спирмена рассчитывается по формуле:
 ,
,
где:  , xi и yi – ранги i -го объекта по переменным Х и Y, n – число пар наблюдений.
, xi и yi – ранги i -го объекта по переменным Х и Y, n – число пар наблюдений.
Зная выборочное значение  , можнопроверить гипотезу о значимости ρ. Нулевая гипотеза формулируется как H 0: ρ=0‒наблюдаемые случайные величины Х и Y некоррелированы, альтернативная ‒ H 1: ρ¹0.
, можнопроверить гипотезу о значимости ρ. Нулевая гипотеза формулируется как H 0: ρ=0‒наблюдаемые случайные величины Х и Y некоррелированы, альтернативная ‒ H 1: ρ¹0.
Для проверки нулевой гипотезы используется соотношение:
 .
.
Значение  рассчитывается с использованием распределения Стъюдента по формуле: = СТЪЮДРАСПОБР(a; k), где a- уровень значимости;
рассчитывается с использованием распределения Стъюдента по формуле: = СТЪЮДРАСПОБР(a; k), где a- уровень значимости;  - число степеней свободы.
- число степеней свободы.
Замечание: при n £10 для оценки значимости следует воспользоваться точными статистическими таблицами.
Если 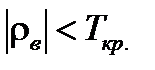 , то коэффициент ранговой корреляции Спирмена незначим.
, то коэффициент ранговой корреляции Спирмена незначим.
Пример 2. Цветные диски, имеющие порядок оттенков 1, 2,…, 15, были расположены испытуемым в следующем порядке:
7, 4, 2, 3, 10, 1, 6, 8, 9, 5, 11, 15, 14, 12, 13.
Охарактеризовать способность испытуемого различать оттенки цветов с помощью коэффициента ранговой корреляции Спирмена между действительными и наблюдаемыми результатами.
Решение
Введём исходные данные в диапазоны A4:A18, B4:B18 и D4:D18.
Рассчитаем ранги действительных и наблюдаемых результатов. Для этого в ячейку C4 введём формулу:
=РАНГ(C4;$C$4: $C$18;1) и протянем её до ячейки С18.
В ячейку E4 введём формулу:
=РАНГ(E4;$E$4: $E$18;1) и протянем её до ячейки E18.
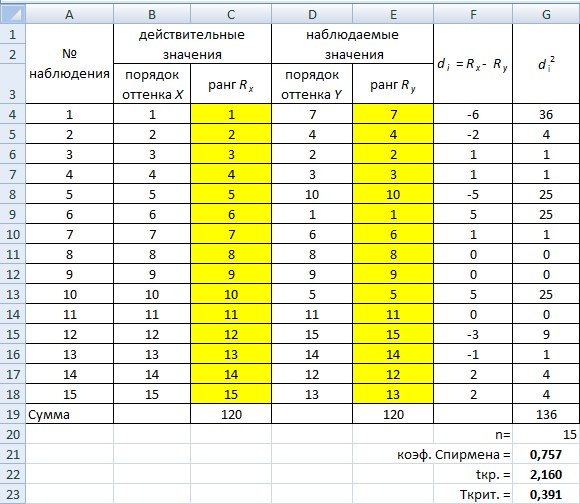
В ячейках C19 и E19 для проверки рассчитаем суммы рангов. Каждая сумма должна быть равна сумме рангов, найденной по формуле:
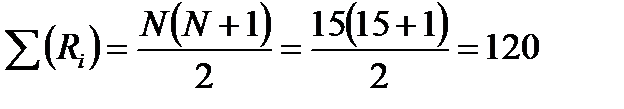 .
.
Рассчитаем разности рангов. Для этого в ячейку F4 введём формулу =C4-E4 и протянем её до ячейки F18.
В диапазоне G4:G18 вычислим квадраты разности рангов.
В ячейке G19 найдём сумму квадратов разности рангов. (равна 136).
В ячейке G21 найдём значение выборочного коэффициента Спирмена по формуле
=1-6/G20/(G20^2-1)*G19.
Получим результат: 0,757.
Оценим значимость коэффициента для уровня значимости a = 0,05. Так как  .= 4,179, то гипотезу о незначимости коэффициента корреляции Спирмена следует отвергнуть: испытуемый способен различать оттенки цветов.
.= 4,179, то гипотезу о незначимости коэффициента корреляции Спирмена следует отвергнуть: испытуемый способен различать оттенки цветов.
Коэффициент ранговой корреляции Кендалла вычисляется следующим образом.
Столбцы  переставляются так, чтобы ранги
переставляются так, чтобы ранги 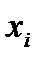 образовывали возрастающую последовательность 1, 2, …, n. Теперь
образовывали возрастающую последовательность 1, 2, …, n. Теперь  = i.
= i.
Для каждого ранга yi обозначим через pi число рангов  , причём
, причём  , и найдём их сумму:
, и найдём их сумму:  .
.
Через qi обозначим число рангов  , причем
, причем  , и вычислим их сумму:
, и вычислим их сумму: 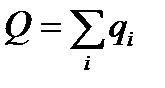 . Тогда S=P-Q. Коэффициент t в вычисляется по одной из эквивалентных формул:
. Тогда S=P-Q. Коэффициент t в вычисляется по одной из эквивалентных формул:

 .
.
Для оценки значимости коэффициента ранговой корреляции Кендалла при n ³10 следует воспользоваться формулой:
 ,
,
где  находится из соотношения:
находится из соотношения:
 .
.
Ф(x) - функция Лапласа.
Если  , то коэффициент ранговой корреляции Кендалла незначим.
, то коэффициент ранговой корреляции Кендалла незначим.
Пример 3. Два эксперта независимо друг от друга оценили 10 студенческих научных работ, представленных на конкурс. Результаты тестирования в баллах представлены в таблице.
| Работа | ||||||||||
| Эксперт 1 | ||||||||||
| Эксперт 2 |
Проверить гипотезу о полной несогласованности (независимости) оценок экспертов, используя коэффициент ранговой корреляции Кендалла при уровне значимости a = 0,05.
Решение
Введём исходные данные в диапазоны A1:A11, B1:B11 и C1:C11.
Рассчитаем ранги оценок первого (диапазон D2:D11) и второго экспертов (диапазон E2:E11).
Выделим диапазон D1:E11, в котором находятся ранги оценок и скопируем его в диапазон F1:G11, используя команду Специальная вставка.
В открывшемся диалоговом окне Специальная вставка в группе переключателей Вставить установить переключатель значения и щёлкнуть на кнопке Ok.
Выделим диапазон F1:G11. Нажать правую кнопку мыши и в контекстном меню выполнить команды Сортировка/Настраиваемая сортировка. В открывшемся диалоговом окне Сортировка установить следующие значения полей: Столбец Сортировать по: Rxi; Сортировка: значения; Порядок: по возрастанию и нажать кнопку Ok. В диапазоне F1:G11появятся ранги оценок экспертов, отсортированные в порядке возрастания рангов оценок первого эксперта.

ВячейкуH2введёмформулумассива =СУММ(ЕСЛИ($G3:$G$11>G2;1:0)), нажмёмклавиши <Ctrl>+<Shift>+<Enter> изатемскопируемэтуформулувячейкиH3:H11.
В ячейке H12 найдём сумму чисел pi. Это будет значение Р.
В ячейке H13 рассчитаем значение выборочного коэффициента ранговой корреляции Кендалла по формуле: =4*H12/(10^2-10)-1. Получим результат: 0,689.
Оценим значимость коэффициента корреляции Кендалла. Рассчитаем  по формуле =НОРМСТОБР(1-0,05/2). Получим 1,96.
по формуле =НОРМСТОБР(1-0,05/2). Получим 1,96.
В ячейку H15введём формулу: =H14*КОРЕНЬ(2*(2*10+5)/9/10/(10-1)).
Получим 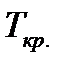 =0,487. Так как
=0,487. Так как  (0,689>0,487), то нулевую гипотезу следует отвергнуть: мнения экспертов не являются независимыми.
(0,689>0,487), то нулевую гипотезу следует отвергнуть: мнения экспертов не являются независимыми.
Корреляционный анализ
Для многомерной выборки рассчитываются ковариационные и корреляционные матрицы.
Исходные данные представляются в виде:

где: i =1,2,…, n ‒ номер наблюдения; j =1,2,…, m ‒номер показателя.
Пример 4. С целью анализа взаимосвязи показателей эффективности производства продукции: производительности труда  , фондоотдачи
, фондоотдачи  и материалоёмкости производства
и материалоёмкости производства 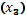 была отобрана группа из десяти однотипных предприятий. Получены данные, приведённые в таблице:
была отобрана группа из десяти однотипных предприятий. Получены данные, приведённые в таблице:
| № предприятия | 
| 
| 
|
| 6,0 | 2,0 | ||
| 4,9 | 0,8 | ||
| 7,0 | 2,7 | ||
| 6,7 | 3,0 | ||
| 5,8 | 1,0 | ||
| 6,1 | 2,1 | ||
| 5,0 | 0,9 | ||
| 6,9 | 2,6 | ||
| 6,8 | 3,0 | ||
| 5,9 | 1,1 |
Рассчитать ковариационную и корреляционную матрицы рассматриваемой совокупности.
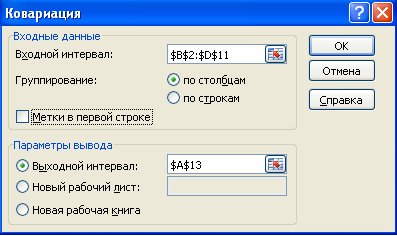 Рассчитаем ковариацию с помощью инструмента пакета анализа «Ковариация».
Рассчитаем ковариацию с помощью инструмента пакета анализа «Ковариация».
Выполним команды Данные®Анализ данных®Ковариация и введём следующие данные. В результате будет выведена ковариационная матрица, на главной диагонали которой находятся выборочные дисперсии, а на побочной - ковариация.

Получим корреляционную матрицу. Выполним команды Данные®Анализ данных®Корреляция и введём следующие данные.

Нажмём кнопку ОК и получим таблицу результатов.
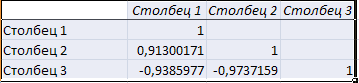
Корреляционная матрица имеет вид:
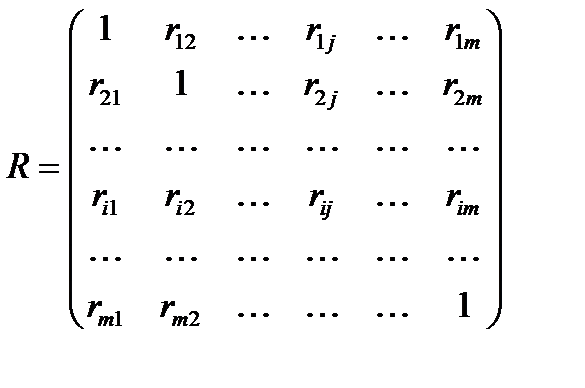
Парный коэффициент корреляции между признаками j и m рассчитывается по формуле:
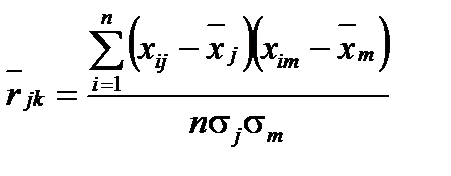
где  - выборочное среднее квадратическое отклонение по признаку
- выборочное среднее квадратическое отклонение по признаку  ;
;  - среднее квадратическое отклонение по признаку xm.
- среднее квадратическое отклонение по признаку xm.
Корреляционная матрица всегда симметрична, на главной диагонали её находятся 1.
Значимость парных коэффициентов можно проверить с помощью критерия Стьюдента.
Показателям тесноты связи можно дать качественную на основе шкалы Чеддока:
| Количественная мера тесноты связи | Количественная характеристика силы связи |
| 0,1-0,3 | Слабая |
| 0,3-0,5 | Умеренная |
| 0,5-0,7 | Заметная |
| 0,7-0,9 | Высокая |
| 0,9-0,99 | Весьма высокая |
Функциональная связь возникает при значении равном 1, а отсутствие связи – 0. При значении показателей тесноты связи меньше 0,7 величина коэффициента детерминации всегда будет ниже 50%. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтёнными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение.