ЛАБОРАТОРНАЯ РАБОТА № 11

ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»

Кафедра общей и технической физики

 

 

МЕХАНИКА

ЛАБОРАТОРНАЯ РАБОТА № 11

 

 

«определение отношения теплоёмкости при постоянном давлении к теплоёмкости при постоянном объёме ДЛЯ воздуха методом стоячей волны»

 

САНКТ-ПЕТЕРБУРГ 2019

 

Цель работы - определить g = C _p/ C_V методом стоячей звуковой волны.

 

Общие сведения

Рассмотрим, как распространяется звуковая волна в закрытой цилиндрической трубе, заполненной воздухом. В момент времени t = 0 мембрана телефона T (рис.1) начинает двигаться вправо с постоянной скоростью . Молекулы воздуха вблизи мембраны придут в движение и тоже будут перемещаться вправо со скоростью . Непосредственно около мембраны возникнет область сжатия, давление внутри которой р = р ₀ + D р, где р ₀ - первоначальное давление воздуха. Сжатый слой воздуха передаст импульс молекулам, расположенным справа, приводя таким образом в движение соседний слой. В течение второй части периода мембрана движется влево, создавая справа от себя область разрежения, в которую устремляются молекулы из сжатого слоя. Таким образом, молекулы воздуха совершают колебательное движение в направлении колебаний мембраны. В среде при этом распространяются, чередуясь, области сжатия и разрежения воздуха (области повышенного и пониженного давления), что и представляет собой бегущую звуковую волну. Звук является продольной волной, т.к. частицы среды совершают колебания вдоль направления распространения. Будем описывать распространение волны с помощью фазовой скорости - скорости распространения в пространстве поверхностей, образованных частицами, совершающими колебания в одинаковой фазе.

 

 

 

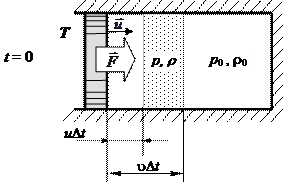Рисунок 1. Распространение звуковой волны в закрытой цилиндрической трубе, заполненной воздухом.

 

 

Импульс силы , с которой мембрана в течение времени D t давит на газ

, (11.1)

где S - площадь мембраны, D p – избыточное давление, обусловленное силой .

С другой стороны, импульс внешней силы равен приращению импульса (количества движения), которое получил газ:

, (11.2)

где - плотность сжатого воздуха; - плотность воздуха в начальный момент времени; - масса сжатого воздуха; 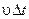- длина столба воздуха (путь, который прошла волна за время 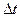). Объединяя равенства (11.1) и (11.2), получим

(11.3)

До движения мембраны масса воздуха m в отрезке трубы длиной 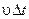составляла . При смещении мембраны на u D t плотность воздуха меняется, и в этом случае его массу можно представить (рис. 1)

,

или

,

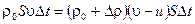После простых алгебраических преобразований получим

(11.4)

Подставив равенство (3) в формулу (4), можно записать

. (11.5)

Если изменения плотности и давления малы (Dr << r₀ и D p << p ₀), то скорость распространения волны

. (11.6)

С точки зрения термодинамики процесс распространения звуковой волны в газе можно рассматривать как адиабатический, так как изменение давления происходит так быстро, что смежные области среды не успевают обмениваться теплом.

Адиабатический процесс описывается уравнением pV ^g = const. Так как V = M/ r (здесь М - масса газа), то p (M/r)^g = const. Продифференцировав это равенство с учётом изменения давления и плотности, получим

,

откуда

,

т.е. в соответствии с формулой (11.6)

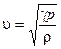, (11.7)

где r - плотность газа при данном давлении и температуре, r = p m /RT; m - молярная масса газа; R - универсальная газовая постоянная; T - абсолютная температура.

Подставив r в уравнение (7), получим

,

откуда

. (11.8)

Таким образом, для вычисления g необходимо определить скорость распространения звуковых колебаний. В работе эта скорость определяется методом стоячей волны.

Если в трубе, один конец которой закрыт, возбудить звуковые колебания, в ней в результате наложения двух встречных волн (прямой и отражённой) с одинаковыми частотами и амплитудами будут возникать стоячие волны. В определенных точках амплитуда стоячей волны равна сумме амплитуд обоих колебаний и имеет максимальное значение; такие точки называются пучностями. В других точках результирующая амплитуда равна нулю, такие точки называются узлами. Расстояние между ближайшим узлом и пучностью равно l/4, где l - длина бегущей звуковой волны. Таким образом, измерив расстояние между узлом и пучностью или между двумя ближайшими пучностями (l/2), можно найти длину бегущей звуковой волны l. Фазовая скорость волны рассчитывается через длину волны по соотношению

u = ln, (11.9)

где n - частота колебаний.

 

 

Порядок выполнения работы

При выполнении работы следует строго соблюдать правила техники безопасности и охраны труда, установленные в лаборатории. Выполнять работу нужно предельно аккуратно, не трясти и не толкать установку, поскольку это может исказить результаты. Работа выполняется в строгом соответствии с нижеизложенным порядком выполнения и в объёме, предусмотренном индивидуальным заданием.

 

Записать в таблицу технические данные прибора:

№ п.п.	Название прибора	Пределы измерений	Число делений	Цена деления	Класс точности	Абсолютная приборная погрешность

 

Описание экспериментальной установки.

В экспериментальную установку (рис.2) входят: стеклянная труба, в которой создаётся стоячая волна, звуковой генератор (ЗГ), микровольтметр, частотомер (Ч). В стеклянную трубу вмонтированы неподвижный микрофон (М) и телефон (Т), который может свободно перемещаться вдоль оси трубы.

 

 

 

Рисунок 2. Экспериментальная установка

 

Звуковой генератор вырабатывает синусоидальное напряжение звуковой частоты, которое подается на телефон. Переменный ток приводит в колебательное движение мембрану телефона, являющуюся излучателем звуковой волны. Отражённая от противоположной стенки трубы волна движется навстречу излучаемой и происходит их наложение. В результате в трубе возникает стоячая звуковая волна. В микрофоне происходит преобразование механической энергии волны в энергию электрического тока, величина которого измеряется микровольтметром. Частота звуковой волны устанавливается лимбом на генераторе, точное значение частоты измеряется частотомером. При перемещении телефона вдоль трубы ток в цепи микрофона будет меняться от минимального, когда микрофон попадает в узел, до максимального, когда он попадает в пучность. Таким образом, следя за показаниями микровольтметра, можно найти положения нескольких пучностей стоячей волны и вычислить ее длину.

Последовательность проведения измерений:

1) включить ЗГ и частотомер в сеть, прогреть приборы в течение 3-5-ти минут;

2) после прогрева установить необходимую частоту колебаний на звуковом генераторе (указанную преподавателем), измеряя точное значение частоты частотомером;

3) перемещая телефон вдоль трубы, найти ближайшее к левому концу трубы положение телефона l_k, при котором показание микровольтметра максимально, записать его в таблицу;

4) зафиксировать все оставшиеся положения, при которых показания микровольтметра максимальны;

5) вычислить разность между соседними отсчётами d l_k=l_k – l_{k – 1} для всех наблюдавшихся пучностей, усреднить полученные значения;

6) по среднему расстоянию между пучностями рассчитать длину бегущей волны l= 2× и скорость по формуле (11.9);

7) повторить пп.3-6 для 4-5-ти значений частоты в интервале 1000-1800 Гц.

8) измерить температуру воздуха в помещении;

9) рассчитать g по формуле (11.8) при m = 2,9×10^-2 кг/моль (воздух), R = 8,31 Дж/(моль×К);

10) результаты измерений и расчётов оформить в виде таблицы:

 

 

Таблица 1.

Физ. величина	n	lk	d lk	l	u	g
Ед. измерения Номер опыта
1.
средние				l = 2×
2.
…
n

 

11) найти среднее значение ;

12) рассчитать погрешность косвенных измерения g.

 

Контрольные вопросы

 

1. Что такое теплоемкость, молярная теплоемкость, удельная теплоемкость? Как они связаны? Какова размерность теплоемкости? От чего зависит молярная теплоемкость?

2. Почему C_p > C_V с точки зрения первого начала термодинамики?

3. Что такое бегущая и стоячая звуковая волна? Каковы ее основные характеристики?

4. Каков механизм распространения звуковой волны?

5. Что представляет собой звуковая волна с точки зрения термодинамики? Каким уравнением и графиками описывается рассматриваемый процесс?

6. От чего зависит скорость распространения звуковой волны?

7. Как связаны между собой частота, длина волны, волновое число и скорость распространения бегущей волны?

8. Напишите выражение для гармонической бегущей волны и убедитесь, что оно является решением волнового уравнения.

9. Напишите выражение для стоячей волны. Как стоячая волна может быть получена из бегущих?

10. Как рассчитать местоположение узлов и пучностей для стоячей волны?

11. Задача. Во сколько раз скорость распространения звука летом (температура +30 ºС) больше скорости распространения звука зимой (температура –30 ºС)?

12. Задача. На расстоянии 510 м от наблюдателя рабочие вбивают сваи с помощью копра. Какое время пройдёт от момента, когда наблюдатель увидит удар копра, до момента, когда он услышит звук удара? Скорость звука в воздухе равна 340 м/с. Ответ выразите в с.