Задачи 1.1 – 1.6. Заданы дискретные ансамбли:
 ;
;  ;
;  .
.
Не вычисляя их энтропий, предсказать какая из них будет больше всех, какая – меньше всех. Проверить предположения, вычислив H(U), H(V) и H(W).
Варианты заданий к задачам 1.2 – 1.6. (к задаче1.1 заданиеприведено в условии):
1.2.  ;
;  :
:  .
.
1.3.  ;
;  ;
;  .
.
1.4.  ;
;  :
:  .
.
1.5.  ;
; 
 .
.
1.6.  ;
;  ;
;  .
.
Задачи 1.7– 1.12. Вычислить энтропию дискретного ансамбля  при условии, что V представляет собой дискретный ансамбль
при условии, что V представляет собой дискретный ансамбль  и
и  – тоже дискретный ансамбль
– тоже дискретный ансамбль 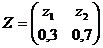 . Решить задачу двумя методами.
. Решить задачу двумя методами.
Варианты заданий к задачам 1.8 – 1.12. (к задаче1.7 заданиеприведено в условии).
1.8.  ;
;  .
.
1.9.  ;
; 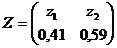 ;
;  .
.
1.10.  ;
;  .
.
1.11.  ;
;  ;
;  .
.
1.12.  ;
;  ;
; 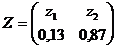 .
.
Задачи 1.13– 1.18. Имеются два дискретных пятеричных (с объемом алфавита  ) источника с независимыми элементами. На выходе каждого источника появляется сообщение одинаковой длины - по
) источника с независимыми элементами. На выходе каждого источника появляется сообщение одинаковой длины - по  элементов. Количество различных элементов
элементов. Количество различных элементов  в сообщении каждого источника постоянно. Сообщения каждого источника отличаются только порядком следования элементов. Зафиксированы два типичных сообщения:
в сообщении каждого источника постоянно. Сообщения каждого источника отличаются только порядком следования элементов. Зафиксированы два типичных сообщения:
0 4 2 3 1 4 3 2 0 1 2 1 0 2 0 3 2 1 4 3 2 0 2 4 1 – первого источника;
0 0 3 1 1 2 1 0 1 4 2 2 0 1 1 0 1 2 3 2 4 1 3 0 1 – второго источника.
Сравнить среднее количество информации, приходящейся на один элемент каждого из источников.
Варианты заданий к задачам 1.14 – 1.18. (к задаче1.13 заданиеприведено в условии):
1.14.  ;
; 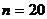 ; 0 3 0 10 2 2 1 3 0 2 0 1 0 1 0 1 0 1 2; 0 3 1 2 2 1 3 0 2 0 1 3 3 1 2 0 1 3 0 2.
; 0 3 0 10 2 2 1 3 0 2 0 1 0 1 0 1 0 1 2; 0 3 1 2 2 1 3 0 2 0 1 3 3 1 2 0 1 3 0 2.
1.15.  ;
;  ; 1 02 5 2 4 2 0 2 3 2 1 2 4 2 5 1 1 2 3 2 2 0 1 2 2 0 2 3 2; 4 0 1 3 2 0 2 1 4 3 3 1 2 0 4 5 5 4 5 0 5 1 3 2 5 4 3 0 2 1.
; 1 02 5 2 4 2 0 2 3 2 1 2 4 2 5 1 1 2 3 2 2 0 1 2 2 0 2 3 2; 4 0 1 3 2 0 2 1 4 3 3 1 2 0 4 5 5 4 5 0 5 1 3 2 5 4 3 0 2 1.
1.16.  ;
; 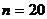 ; 2 4 1 4 0 4 2 4 1 4 3 4 0 4 2 4 1 4 2 4; 0 4 1 3 2 1 0 3 2 4 4 0 3 1 2 1 4 2 0 3.
; 2 4 1 4 0 4 2 4 1 4 3 4 0 4 2 4 1 4 2 4; 0 4 1 3 2 1 0 3 2 4 4 0 3 1 2 1 4 2 0 3.
1.17.  ;
;  ; 6 0 6 1 6 5 6 2 6 3 2 6 2 6 0 6 2 6 5 0 6; 0 6 1 5 2 4 3 6 1 5 0 4 2 3 3 0 4 1 5 2 6.
; 6 0 6 1 6 5 6 2 6 3 2 6 2 6 0 6 2 6 5 0 6; 0 6 1 5 2 4 3 6 1 5 0 4 2 3 3 0 4 1 5 2 6.
1.18.  ;
;  ; 5 1 5 7 5 3 5 5 5 2 6 4 5 4 2 7 5 2 5 6 5 7 5 0; 0 7 5 3 2 6 4 2 0 3 1 4 2 5 3 7 7 6 5 4 0 3 1 2.
; 5 1 5 7 5 3 5 5 5 2 6 4 5 4 2 7 5 2 5 6 5 7 5 0; 0 7 5 3 2 6 4 2 0 3 1 4 2 5 3 7 7 6 5 4 0 3 1 2.
Задачи 1.19– 1.24. Задан дискретный ансамбль  . Не пользуясь калькулятором и таблицей логарифмов, оценить сверху (т.е. указать число, которое достаточно близко к H(U) и наверняка больше H(U)) энтропию ансамбля U. Доказать, что полученная оценка является оценкой сверху Сравнить оценку с истинным значением H(U).
. Не пользуясь калькулятором и таблицей логарифмов, оценить сверху (т.е. указать число, которое достаточно близко к H(U) и наверняка больше H(U)) энтропию ансамбля U. Доказать, что полученная оценка является оценкой сверху Сравнить оценку с истинным значением H(U).
Варианты заданий к задачам 1.20 – 1.24. (к задаче1.19 заданиеприведено в условии):
1.20.  ;
;
1.21.  .
.
1.22.  .
.
1.23.  .
.
1.24.  .
.
Задачи 1.25– 1.30. Распределение вероятностей дискретной случайной величины имеет вид: p (x 1)=0,470933; p (x 2)=0,1; p (x 3)=0,1; p (x 4)=0,1; p (x 5)=0,1; p (x 6)=0,01; p (x 7)=0,01; p (x 8)=0,109067. Определить число n значений случайной величины, при которых энтропия H p(X) равномерного распределения будет равна энтропии H (X) заданного распределения.
Варианты заданий к задачам 1.26 – 1.30. (к задаче1.25 заданиеприведено в условии):
1.26. p (x 1)=0,362133; p (x 2)=0,15; p (x 3)=0,15; p (x 4)=0,1; p (x 5)=0,1; p (x 6)=0,1; p (x 7)=0,01; p (x 8)=0,01; p (x 9)=0,017867.
1.27. p (x 1)=0,477446; p (x 2)=0,14; p (x 3)=0,2; p (x 4)=0,1; p (x 5)=0,082554.
1.28. p (x 1)=0,099124; p (x 2)=0,11; p (x 3)=0,1; p (x 4)=0,1; p (x 5)=0,1; p (x 6)=0,01; p (x 7)=0,01; p (x 8)=0,470876.
1.29. p (x 1)=0,400355; p (x 2)=0,12; p (x 3)=0,1; p (x 4)=0,1; p (x 5)=0,1; p (x 6)=0,09; p (x 7)=0,07; p (x 8)=0,019645.
1.30. p (x 1)=0,102584; p (x 2)=0,12; p (x 3)=0,1; p (x 4)=0,1; p (x 5)=0,1; p (x 6)=0,09; p (x 7)=0,07; p (x 8)=0,317416.
Задачи 1.31– 1.40. Ансамбли событий X и Y объединены, причем вероятности совместных событий равны:  ;
;  ;
;  ;
;  ;
; 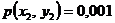 ;
;  . Найти: энтропии ансамблей X и Y соответственно
. Найти: энтропии ансамблей X и Y соответственно 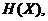
 ; энтропию объединенного ансамбля
; энтропию объединенного ансамбля  ; условные энтропии ансамблей
; условные энтропии ансамблей 
Варианты заданий к задачам 1.32 – 1.40. (к задаче1.31 заданиеприведено в условии):
1.32.  ;
;  ;
;  ;
;  ;
; 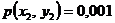 ;
;  .
.
1.33.  ;
;  ;
;  ;
;  ;
; 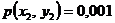 ;
;  .
.
1.34.  ;
;  ;
;  ;
;  ;
;  ;
;  .
.
1.35.  ;
; 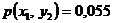 ;
;  ;
;  ;
; 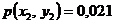 ;
;  ;.
;.  ;
;  ;
;  .
.
1.36.  ;
;  ;
;  ;
;  ;
;  ;
;  ;.
;.  ;
;  ;
;  .
.
1.37.  ;
;  ;
;  ;
;  ;
;  ;
; 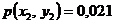 ;
;  ;
;  .
.
1.38.  ;
; 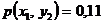 ;
;  ;
; 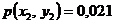 ;
; 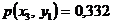 ;
;  ;
;  ;
;  .
.
1.39.  ;
;  ;
;  ;
; 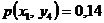 ;
;  ;
;  ;
;  ;
;  .
.
1.40.  ;
;  ;
;  ;
; 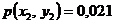 ;
;  ;
;  ;
;  ;
;  .
.
Задачи 1.41– 1.50. Найти энтропию шума  в двоичном симметричном канале без памяти, если энтропия источника на входе канала
в двоичном симметричном канале без памяти, если энтропия источника на входе канала  бит, энтропия ансамбля на выходе канала
бит, энтропия ансамбля на выходе канала  бит, ненадежность канала
бит, ненадежность канала 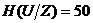 бит.
бит.
Варианты заданий к задачам 1.42 – 1.50. (к задаче 1.41 заданиеприведено в условии):
1.42.  бит;
бит;  бит;
бит;  бит.
бит.
1.43.  бит;
бит;  бит;
бит;  бит.
бит.
1.44. 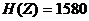 бит;
бит;  бит;
бит;  бит.
бит.
1.45.  бит;
бит;  бит;
бит;  бит.
бит.
1.46. 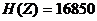 бит;
бит;  бит;
бит;  бит.
бит.
1.47. 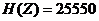 бит;
бит;  бит;
бит;  бит.
бит.
1.48. 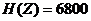 бит;
бит;  бит;
бит; 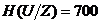 бит.
бит.
1.49.  бит;
бит;  бит;
бит;  бит.
бит.
1.50.  бит;
бит;  бит;
бит;  бит.
бит.
Задачи 1.51– 1.60. Элементы множеств X и Y статистически связаны. Известно, что H(X)=10 бит, H(Y)=14 бит. В каких пределах меняется условная энтропия  при изменении
при изменении  в максимально возможных пределах.
в максимально возможных пределах.
Варианты заданий к задачам 1.52 – 1.60. (к задаче 1.51 заданиеприведено в условии):
1.52.  бит;
бит;  бит.
бит.
1.53.  бит;
бит; 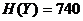 бит.
бит.
1.54.  бит;
бит;  бит.
бит.
1.55.  бит;
бит;  бит.
бит.
1.56.  бит;
бит;  бит.
бит.
1.57.  бит;
бит;  бит.
бит.
1.58.  бит;
бит;  бит.
бит.
1.59.  бит;
бит;  бит.
бит.
1.60.  бит;
бит; 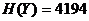 бит.
бит.
Задачи 1.61– 1.75. Принимаемый сигнал может иметь амплитуду А1 (событие Х1) или А2 (событие Х2), а также сдвиг фазы  (событие
(событие  ) или
) или 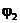 (событие
(событие  ) режимах. Вероятности совместных событий имеют следующие значения:
) режимах. Вероятности совместных событий имеют следующие значения:  ;
;  ;
; 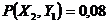 ;
;  .
.
Вычислить количество информации, получаемой о фазовом сдвиге сигнала, если станет известной его амплитуда.
Варианты заданий к задачам 1.62 – 1.75. (к задаче 1.61 заданиеприведено в условии):
1.62.  ;
;  ;
;  ;
;  .
.
1.63.  ;
;  ;
; 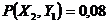 ;
;  .
.
1.64.  ;
;  ;
;  ;
;  .
.
1.65. 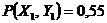 ;
;  ;
;  ;
;  .
.
1.66.  ;
;  ;
;  ;
;  .
.
1.67.  ;
;  ;
; 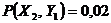 ;
; 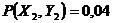 .
.
1.68.  ;
;  ;
;  ;
; 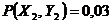 .
.
1.69.  ;
;  ;
;  ;
;  .
.
1.70.  ;
;  ;
;  ;
;  .
.
1.71.  ;
;  ;
;  ;
;  .
.
1.72.  ;
;  ;
;  ;
;  .
.
1.73. 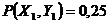 ;
;  ;
;  ;
;  .
.
1.74.  ;
;  ;
;  ;
;  .
.
1.75.  ;
;  ;
; 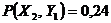 ;
;  .
.
Задачи 1.76 – 1.90. Дискретный источник выбирает сообщения из ансамбля  . Длительности сообщений соответственно равны: tu1 =8 c, tu2 =6 c, tu3 =5 c, tu4 =3 c. Определить производительность источника.
. Длительности сообщений соответственно равны: tu1 =8 c, tu2 =6 c, tu3 =5 c, tu4 =3 c. Определить производительность источника.
Варианты заданий к задачам 1.77 – 1.90. (к задаче 1.76 заданиеприведено в условии):
1.77.  ; tu1 =0,3 c, tu2 =0,5 c, tu3 =0,1 c, tu4 =0,14 c.
; tu1 =0,3 c, tu2 =0,5 c, tu3 =0,1 c, tu4 =0,14 c.
1.78.  ; tu1 =0,13 c, tu2 =0,25 c, tu3 =0,31 c, tu4 =0,42 c.
; tu1 =0,13 c, tu2 =0,25 c, tu3 =0,31 c, tu4 =0,42 c.
1.79.  ; tu1 =0,4 c, tu2 =0,2 c, tu3 =0,6 c, tu4 =0,17 c.
; tu1 =0,4 c, tu2 =0,2 c, tu3 =0,6 c, tu4 =0,17 c.
1.80.  ; tu1 =0,34 c, tu2 =0,63 c, tu3 =0,41 c, tu4 =0,23 c.
; tu1 =0,34 c, tu2 =0,63 c, tu3 =0,41 c, tu4 =0,23 c.
1.81.  ; tu1 =0,35 c, tu2 =0,27 c, tu3 =0,83 c, tu4 =0,23 c.
; tu1 =0,35 c, tu2 =0,27 c, tu3 =0,83 c, tu4 =0,23 c.
1.82.  ; tu1 =0,3 c, tu2 =0,57 c, tu3 =0,44 c, tu4 =0,1 c.
; tu1 =0,3 c, tu2 =0,57 c, tu3 =0,44 c, tu4 =0,1 c.
1.83.  ; tu1 =0,2 c, tu2 =0,9 c, tu3 =0,5 c, tu4 =0,4 c.
; tu1 =0,2 c, tu2 =0,9 c, tu3 =0,5 c, tu4 =0,4 c.
1.84.  ; tu1 =0,96 c, tu2 =0,44 c, tu3 =0,67 c, tu4 =0,39 c.
; tu1 =0,96 c, tu2 =0,44 c, tu3 =0,67 c, tu4 =0,39 c.
1.85.  ; tu1 =0,36 c, tu2 =0,79 c, tu3 =0,73 c, tu4 =0,22 c.
; tu1 =0,36 c, tu2 =0,79 c, tu3 =0,73 c, tu4 =0,22 c.
1.86. 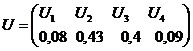 ; tu1 =0,55 c, tu2 =0,48 c, tu3 =0,83 c, tu4 =0,29 c.
; tu1 =0,55 c, tu2 =0,48 c, tu3 =0,83 c, tu4 =0,29 c.
1.87. 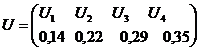 ; tu1 =0,43 c, tu2 =0,26 c, tu3 =0,09 c, tu4 =0,93 c.
; tu1 =0,43 c, tu2 =0,26 c, tu3 =0,09 c, tu4 =0,93 c.
1.88. 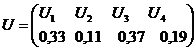 ; tu1 =0,45 c, tu2 =0,33 c, tu3 =0,71 c, tu4 =0,01 c.
; tu1 =0,45 c, tu2 =0,33 c, tu3 =0,71 c, tu4 =0,01 c.
1.89.  ; tu1 =0,11 c, tu2 =0,32 c, tu3 =0,19 c, tu4 =0,03 c.
; tu1 =0,11 c, tu2 =0,32 c, tu3 =0,19 c, tu4 =0,03 c.
1.90.  ; tu1 =0,3 c, tu2 =0,8 c, tu3 =0,01 c, tu4 =0,7 c.
; tu1 =0,3 c, tu2 =0,8 c, tu3 =0,01 c, tu4 =0,7 c.