КОНТРОЛЬНАЯ РАБОТА №2 (2 семестр)

МЕТОДИЧЕСКИЕ УКАЗАНИЯ.

Колебания и волны

Уравнение колебательного процесса s = A cos (ωt+φ)

Уравнение механического осциллятора ϋ + ω² υ = o,

где υ – колеблющаяся величина

Основные законы и формулы акустики

Уровень звукового давления L_p = 20 lg P/P_o

Скорость распространения звука в газах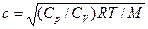

Принцип Доплера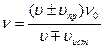

Основные законы и формулы оптики

Показатель преломления среды (абсолютный) n = c/v

Оптическая длина пути L = n r

Оптическая разность хода двух световых волн D = L₁ - L₂

Условие для оптической разности хода при

интерференции:

для максимума D =± 2k l/2 k = 0,1,2..

для минимума D =±(2k±1)l/2 k=0,1,2..

Условие дифракционных максимумов от одной a×sin j =(2k+1) l/2

щели

Условие дифракционных минимумов от одной a×sin j = 2k l/2

щели

Условие главных максимумов дифракционной с×sin j = k l

решетки

Постоянная дифракционной решетки d = a + b

Формула Вульфа - Брэгга для дифракции 2d sin q = kl

рентгеновских лучей

Разрешающая сила дифракционной решетки R = l/Dl = kN

Энергия фотона e = hn = hc/l

Масса фотона m_ф = e/с² = hn/с² =h/cl

Импульс фотона р_ф = m_ф/с = hn/с =h/l

Закон смещения Вина l_мах= b/T

Уравнение Эйнштейна для фотоэффекта e = hn = А + mv²/2

Красная граница фотоэффекта n_гр = А/h или l_гр =hc/A

Изменение длины волны при эффекте Dl = h(1-cosq)/m₀c =

Комптона =L(1-cosq) = 2Lsin²q/2

Основные законы и формулы атомной и ядерной физики

Длина волны де Бройля l =h/p = h/mv

Закон радиоактивного распада N = N₀ e^-lt

Дефект массы ядра Dm = Zm_p +(A - Z)m_n - m_я

Энергия связи ядра Е =Dm с²; E = 931Dm,

где Е выражена в МэВ

Удельная энергия связи ядер e_уд= Е/А

 

ПРИМЕРЫРЕШЕНИЯ ЗАДАЧ

Пример 1. Фокусное расстояние стеклянной (n = 1,5) собирающей линзы равно 0,1 м. Как изменится фокусное расстояние этой линзы в воде (n₁ = 1,33), каково это расстояние?

Решение. СИ

n = 1,5

n₁ = 1,33

________________________________

Определить: F₂ =?

Для линзы, находящейся в воздухе, фокусное расстояние определяется по формуле:

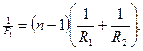
Для линзы, погруженной в воду, формула фокусного расстояния будет иметь вид:

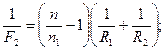
Отношение фокусных расстояний линзы в воздухе и воде определяется из отношения вышеприведенных выражений:

.

Подставляя данные в приведенное выражение, получим:

.

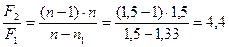Фокусное расстояние в воде определим как F₂= F₁∙ .

Ответ: Фокусное расстояние линзы в воде измениться 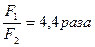, Фокусное расстояние в воде составит F₂ = 0,44 м.

 

Пример 2. Какой угол образуют плоскости поляризации двух николей, если свет, вышедший из второго николя, был ослаблен в 5 раз? Учесть, что поляризатор поглощает 10%, а анализатор 8% падающего на них света.

Решение. СИ

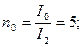
K₁ = 0,1;

K₂ = 0,08.

____________________________________

Определить: φ =?

Естественный луч света 1, падая на грань призмы николя, претерпевает двойное лучепреломление. В результате два луча: обыкновенный 2 и необыкновенный 3 (см. рис. 3.1). Оба луча поляризованы во взаимно перпендикулярных плоскостях, интенсивность их одинакова и равна половине интенсивности естественного света.

 

 

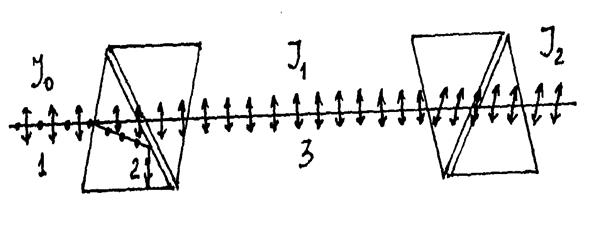
Рис. 3.1.

Интенсивность света, прошедшего через первую призму (поляризатор) с учетом поглощения, равна:

(1)

где I₀ – интенсивность естественного света 1, падающего на первый николь; K₁ = 0,1 – относительная потеря интенсивности света в поляризаторе.

Поляризованный свет 3, попадая на вторую призму (анализатор), вновь испытывает поглощение, но, кроме этого, его интенсивность уменьшится из-за несовпадения плоскостей поляризации поляризатора и анализатора. Это уменьшение интенсивности определяется законом Малюса: I₂ = I cos²φ. Учитывая потери интенсивности света в анализаторе, имеем:

(2)

где K₂ = 0,08 – относительная потеря интенсивности в анализаторе;

φ – угол между плоскостями поляризации поляризатора и анализатора.

Так как, по условию задачи известно, что относительное уменьшение интенсивного света , то подставив значение (2), получим

(3)

Из соотношения (3) получим:

Подставляя данные, проводим вычисления:

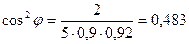
Следовательно, искомый угол φ = 48⁰.

Ответ: Угол между плоскостями поляризации двух николей φ = 48⁰.

 

 

Пример 3. Глухая кирпичная стена имеет размеры: длина - 5 м, высота - 3.0 м, толщина - 50 см (2 кирпича). Рассчитать поток тепла, если внутренняя температура стены - +18⁰С, а наружная - -20⁰С. Определить количество тепла уходящее через стену за 1с и за 1час. Оценить мощность теплового источника, требуемого для компенсации потерь тепла. Теплопроводность кирпича 0.8 Вт/м×К

Решение CИ

l = 5 м - “ -

h = 2.7 м - “ -

d = 50 см 0.5 м

t₁ = +18⁰C T₁ =291 K

t₂ = -20⁰C T₂ =253 K

l = 0.8 Вт/м К - “ –

_____________

Q₁ =?

Поток тепла через поверхность q (количество энергии передающееся через единицу площади [1 м²] за 1c) определяется законом Фурье:

¶ T

q = - l ¾¾¾ (1)

¶ х

где l - коэффициент теплопроводности.

Градиент температуры на поверхности стены ¶ T/¶ х можно оценить как:

 

¶ T T₂ - T₁ 253 -291

¾¾ » ¾¾¾¾ = ¾¾¾¾ = - 76 К/м (2)

¶ х х₂ - х₁ 0.5

Тогда:

q = - 0.8 (- 76) = 60.8 Дж/м²с

Все количество тепла через поверхность площадью S за время t будет определяться формулой:

Q = q S t (3)

За время t₁= 1c через стену проходит количество тепла Q₁:

Q₁ = qSt₁ = 60.8×5×3×1 = 912 = 9.12×10² Дж. (4)

За время t₂= 1чаc=3600 с через стену проходит количество тепла Q₂:

Q₂ =qSt₂ = 60.8×5×3×3600 = 3283200 » 3.28×10⁶ Дж (5)

Мощность источников тепла для компенсации потерь через эту стену должна быть:

N = Q/t = qS = 60.8×5×3 = 912 Вт (6)

Проверка размерности:

[Q] = [q][S][t] =(Дж/м²с) (м²) (с) = Дж

[N] = [q][S] = (Дж/м²с)(м²) = Дж/с = Вт

Ответ: Q₁ = 912 Дж, Q₂ =3.28×10⁶ Дж, N = 912 Вт.

 

Пример 4. Движущийся по реке теплоход дает свисток частотой ν= 400 Гц. Наблюдатель, стоящий на берегу, воспринимает звук свистка частотой ν= 395 Гц. Принимая скорость звука υ= 340 м/с, определить скорость движения теплохода. Приближается или удаляется теплоход?

Решение CИ

ν₀ = 400 Гц

ν = 395 Гц

υ = 340 м/с

_____________

υ_т =?

Акустический эффект Доплера записывают в общем виде:

,

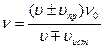Где υ_пр и υ_ист - проекции скоростей источника и приемника по оси Х, положительное направление которой совпадает с направлением распространения звука.

Применяя эффект Доплера к задаче, запишем выражение для определения скорости источника звука:

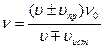, верхний знак – сближение; нижний знак – удаление.

Так как наблюдатель (приемник звука) неподвижен, υ_пр = 0. Подставляя полученное выражение в общую формулу, и проводя преобразования получаем:

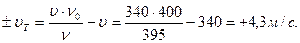
Ответ: Скорость теплохода υ_т = 4,3 м/с, теплоход удаляется.

 

Пример 5. Определить расстояние между атомными плоскостями в кристалле каменной соли, если дифракционный максимум первого порядка наблюдается при падении рентгеновских лучей с длиной волны 0,147 нм под углом 15⁰12^' к поверхности кристалла..

Решение.

l = 0.147 нм

q = 15⁰12^'

k = 1

___________ Рис.3

Найти: d =?.

Дифракция рентгеновских лучей на кристаллах - это результат интерференции рентгеновского излучения, зеркально отражающегося от системы параллельных плоскостей, которые проходят через узлы - атомы кристаллической решетки. Эти плоскости называют атомными плоскостями /рис 3/. Отражение наблюдается лишь в тех направлениях, соответствующих дифракционным максимумам, которым удовлетворяет соотношение:

D = ½BC½ +½BD½= 2d sinq или 2d sinq = k l (1)

где k = 1,2,3... - порядок дифракционного максимума;

q - угол скольжения, т.е. угол между падающим лучом и плоскостью

кристалла;

d - между соседними плоскостями, называемое межплоскостным.

Исходя из условия (1) и учитывая, что k= 1, имеем:

l 1.47×10^{-10 м}

d = ¾¾¾ = ¾¾¾¾¾¾ = 2.82 × 10^{-10 м} = 0.282 нм.

2 sinq 2 sin 15⁰12^'

Ответ: Расстояние между атомными плоскостями d = 0.282 нм.

Пример 6. При анализе содержания сахара используется явление вращения плоскости поляризации света. Определить процентное содержание сахара в кювете длиной 1дм., если плоскость поляризации света повернулась после прохождения раствора на угол φ = 8⁰ . Постоянная вращения сахара α =660 град\м

Решение CИ

L = 1 дм L = 0,1 м

φ = 8⁰

[α] =660 град/м

_________________

Определить: С(%)

Угол поворота плоскости поляризации света после прохождения раствора

длиной L пропорционален длине пути света и концентрации раствора С:

φ = [α] С L, где [α] – удельное вращение.

Поэтому концентрация сахара равна:

φ 8⁰

С = ¾¾¾ = ¾¾¾¾¾¾¾¾¾ =0,121 = 12,1 %

[α] L 660 град/м × 0,1 м

 

Ответ: концентрация сахара С = 12,1 %

 

Пример 7. Определить, сколько ядер в 1 г радиоактивного стронция ⁹⁰Sr₃₈ распадается в течение одного года.

m = 10^{-3 кг}

Т_1/2 = 27 лет

t = 1 год

_____________

N_t=?

Решение.

Для определения числа атомов, содержащихся в 1 г ⁹⁰Sr₃₈

используем соотношение N = nN_A = m/m N_A, где N_A постоянная Авогадро,

n - число молей в изотопе стронция,

m- молярная масса изотопа.

Для изотопа стронция ⁹⁰Sr₃₈ молярная масса m = 90 × 10^-3 кг/моль

Используем закон радиоактивного распада:

N =N₀ e^-lt (2)

где N₀ - начальное число ядер нераспавшихся в момент t = 0

N - число нераспавшихся ядер в момент t;

l - постоянная радиоактивного распада;

e^-lt = eхp - lt - экспоненциально затухающая функция.

Количество распавшихся ядер ⁹⁰Sr₃₈ в течение 1 года:

N_t =N₀ - N = N₀ (1 - e^-lt) (3)

Учитывая, что постоянная радиоактивного распада связана с периодом полураспада соотношением l =(ln 2)/T_1/2,получим:

N_t = N₀ [1 - eхp - (t ln2)/T_1/2 ] (4)

Подставляя (1) в выражение (4), имеем:

N_t = N_A(m/m)[ 1 - eхp - (t ln2)/T_1/2 ] (5)

Произведя вычисления по формуле (5), найдем:

N_t = 6.02×10²³ × 10^-3×(90×10^-3) [1 - eхp (- 0.693 × 1/27)] = 6.4×10²¹ ядер.

Проверим размерность:

[N_t] = моль^-1× кг×(кг/моль)^-1 = - безразмерно.

Ответ: N_t = 6.4×10²¹ ядер.

 

Пример 10. Вычислить дефект массы, энергию связи ядра ⁷Li₃ и удельную энергию связи в

этом ядре.

⁷Li₃

_____________

Dm =?

Е =?

e_уд =?

 

Решение. Масса ядра всегда меньше суммы масс свободных (находящихся вне ядра) протонов и нейтронов, из которых ядро образовалось. Дефект массы ядра Dm и есть разность между суммой масс свободных нуклонов (протонов и нейтронов) и массой ядра:

Dm = Zm_p + (A - Z)m_n - m_я (1),

где Z - атомный номер (число протонов в ядре);

А - массовое число (число нуклонов, составляющих ядро);

m_p,m_n,m_я - массы протона, нейтрона и ядра соответственно.

В справочных таблицах всегда даются массы нейтральных атомов, но не ядер, поэтому формулу (1) следует преобразовать так, чтобы в нее входила масса m_а нейтрального атома. Можно считать, что масса нейтрального атома равна сумме масс ядра и электронов, составляющих электронную оболочку атома:

m_а=m_я+Zm_е т.е: m_я=m_а-Zm_е (2).

Выразив в равенстве (1) массу ядра по формуле (2), получаем:

Dm = Zm_p + (A - Z)m_n - m_а + Zm_е = Z(m_p + m_e) + (A - Z)m_n - m_a (3)

Замечая, что сумма масс протона и электрона равна массе водорода m_p+m_e=m_H, окончательно находим

Dm = Zm_Н + (A - Z)m_n - m_a (4)

Подставив в выражение (4) числовые значения масс (см. табл. 2), получим:

Dm = [ 3×1.00783 + (7-3)×1.00867 -7.01601] а.е.м. = 0.04216 а.е.м.

В соответствии с законом массы и энергии

Е = с²×Dm (5),

где с - скорость света в вакууме.

В системе СИ коэффициент пропорциональности с² равен:

с² = 9×10¹⁶ м²/с² =9×10¹⁶Дж/кг

В ядерной физике используются внесистемные единицы, в которых энергия измеряется в мегаэлектрон-вольтах (МэВ), а масса в атомных единицах массы (а.е.м.):

с² = 931 МэВ/а.е.м.

Во внесистемных единицах формула (5) для энергии связи принимает вид:

Е = 931 Dm (МэВ) (6)

Подставив найденное значение дефекта массы ядра в формулу (6) получим:

Е = 931×0.04216 = 39.2 МэВ

Удельная энергия связи e_уд - это энергия связи приходящаяся на один нуклон в ядре:

e_уд= Е/А = 39.2/7 =5.6 МэВ/нуклон.

Ответ: Dm = 0.04216 а.е.м., Е = 39.2 МэВ, e_уд = 5.6 МэВ/нуклон.