Степень статической неопределимости рамы (рис. 25) по методу перемещений зависит от числа возможных угловых и линейных смещений:
n = 1уг + 1л = 2.
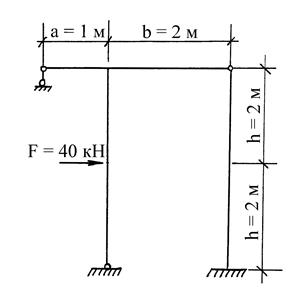
Рис. 25. Расчетная схема заданной рамы.
Выбираем основную систему, вводя дополнительные связи в места возможных смещений (рис. 26). Принимаем условие – реактивные усилия во введенных связях равны нулю.
Канонические уравнения метода перемещений имеют следующий вид:

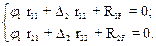
Строим единичные 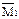 ,
, 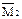 и грузовую МF эпюры моментов с помощью специально разработанных таблиц, которые приведены во всех источниках основной литературы (см. рис. 26).
и грузовую МF эпюры моментов с помощью специально разработанных таблиц, которые приведены во всех источниках основной литературы (см. рис. 26).
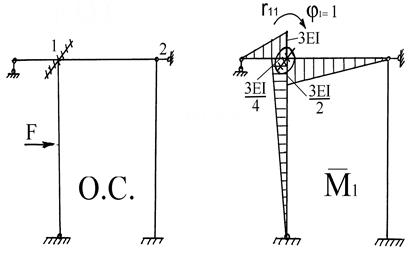
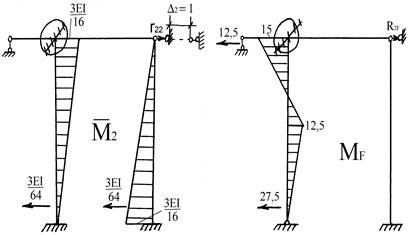
Рис. 26. Основная система, единичные и грузовая эпюры.
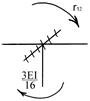
Коэффициенты и свободные члены уравнений находим статическим способом, вырезая соответствующие узлы рамы.

| r11 – 3EI – 0,75EI – 1,5EI = 0; r11 = 5,25EI. |
| 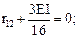
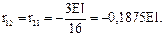
|
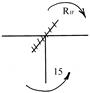
| R1F – 15 = 0; R1F = 15. |
Sx = 0; 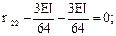
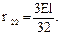
Sx = 0; 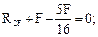
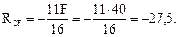
Решаем систему уравнений:


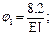
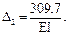
Умножаем эпюру 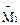 на j1, эпюру
на j1, эпюру  на D2 и получаем так называемые исправленные эпюры (рис. 27).
на D2 и получаем так называемые исправленные эпюры (рис. 27).
Рис. 27. Исправленные единичные эпюры.
Расчетную эпюру Мрасч строим способом сложения, используя выражение
Мрасч =  j1 +
j1 + 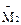 D2 + МF.
D2 + МF.
Имея правильно построенную эпюру Мрасч, можно, рассматривая статическое равновесие всех участков рамы как отдельно взятых статически неопределимых балок, определить продольные и поперечные силы и построить эпюры N и Q (рис. 28).
Задача 6. Рассчитать подпорную стену по данным табл. 6 и схемы, показанной на рис. 29, 30.
Последовательность решения задачи:
1. графическим методом определить активное давление грунта на участки напорной грани стены и участок подпорной грани;
2. построить эпюры интенсивности давления грунта на участки напорной грани стены и участок подпорной грани;
3. определить все силы, действующие на стену, точки их приложения и направления;
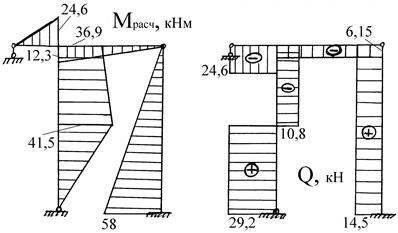
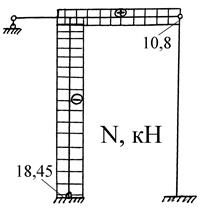
Рис. 28. Расчетные эпюры М, Q, N.
4. построить многоугольник давления сил в стене, определить графически эксцентриситеты в характерном сечении согласно излому профиля стены и в подошве основания подпорной стенки;
5. проверить устойчивость стены на опрокидывание и сдвиг. Коэффициент трения кладки по грунту в плоскости подошвы фундамента принять равным f = 0,45;
6. определить нормальные напряжения сжатия в плоскости подошвы фундамента стены и построить эпюру напряжений.
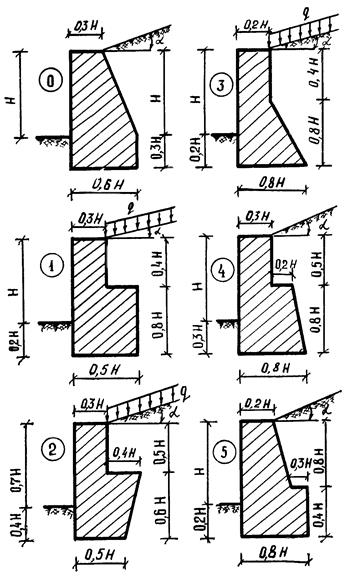
Рис. 29. Расчетные схемы к задаче 6.
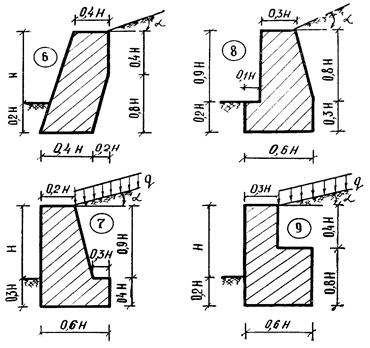
Рис. 30. Расчетные схемы к задаче 6.
Т а б л и ц а 6. Исходные данные к задаче 6
| Номер строки | H, м | Угол α | γкладки, кН/м3 | γгрунта, кН/м3 | Угол φ | Угол φ0 | q, кН/м2 | Номер профиля |
| 12º | 26º | 16º | ||||||
| 14º | 28º | 7º | ||||||
| 9º | 30º | 11º | ||||||
| 13º | 33º | 10º | ||||||
| 10º | 31º | 12º | ||||||
| 7º | 29º | 15º | ||||||
| 8º | 27º | 14º | ||||||
| 10º | 35º | 12º | ||||||
| 9º | 34º | 9º | ||||||
| 8º | 32º | 6º | ||||||
| *** | а | б | в | а | б | в | а | в |