Логическое и функциональное программирование.

Функциональное программирование связывают обычно с языком Лисп и его диалектами, а логическое программирование с языком Пролог и его разновидностями.

ЛИСП (list proccessing – обработка списков) – является языком функций. Это означает, что конструкция, которая может быть записана на языке ЛИСП, является функцией.

Математическим аппаратом, на котором базируется язык Лисп, является l - исчисление. Основным понятием в l - исчислении является понятие функции (отсюда функциональное программирование). Функция f сопоставляет по крайней мере один объект f(x₁,x₂,…,x_n), т.е. ее значение, с каждой n-ной объектов – х₁,х₂,…,х_n, т.е. аргументами, которые, в свою очередь, могут рассматриваться как функции.

Примером может служить выражение (X-Y), которое может рассматриваться либо как функция (f) от х, либо как функция (g) от y. Для того, чтобы различать эти функции, используется символ (l) (отсюда l - исчисление):

f = lx×x-y; g = ly×y-x.

В этих выражениях префикс (l) абстрагирует функции (f) и (g) от самого выражения – (X-Y).

Для функции f(0) = 0-y, а для функции f(1) = 1-y, которые в l - обозначениях примет вид:

(lx×x-y)(0) = 0-y; а

(lx×x-y)(1) = 1-y.

для обозначения функций от нескольких переменных, например h(x,y) = x-y; можно использовать запись lxy×x-y = h, но можно использовать функции, аргументами которых являются также функции. Например, h* = lx×(ly×x-y), которая для каждого числа (а) принимает вид (a,b), принимает вид:

(h*(a))(b) = (ly×(a-y))(b) = a-b.

Т.е. достаточно определять, вообще говоря только функции от одной переменной.

Примером может являться l - исчисление lАВ×(А²-В²), которое вычисляет разность квадратов двух чисел (А и В), и которое записывается в языке ЛИСП как

(Lambda (A B) Difeerence (Times A A)(Times B B))).

В частном, если задать на языке ЛИСП входную строку

(Lambda (A B) Difeerence (Times A A)(Times B B))) (6 3),

то результаты работы ЛИСП – системы будет число 27, т.к. AB×(A²-B²) = 6²-3² = 27.

Логическое программирование – это один из подходов к информатике, при котором в качестве языка высокого уровня используется ПРОЛОГ, основывающийся на логике предикатов первого порядка в форме фраз Хорна.

В ПРОЛОГ’е и его диалектах применяется программная технология, основывающаяся на правиле вывода путем резолюции, которое предложил (американский) профессор Робинсон.

Сфера применения ПРОЛОГ’а, как и ЛИСП’а находится, прежде всего, в разработках по искусственному интеллекту, но ПРОЛГ также используется для таких прикладных задач интерфейсы баз данных, системы поддержки принятия решений, экспертные системы, системы обработки естественного языка и др.

Измеряется скорость работы различных версий ПРОЛОГ’а в числе логических выводов в секунду (Л.В.С.) – по английски параметр обозначается как LIPS – Logical Inferences Per Second (не путать с LISP’ом). Первые версии ПРОЛОГ’а работали со скоростью от 1000¸10 Клвс, в настоящее время разрабатываются со скоростью до 600 Клвс.

Выбор между языками ЛИСП и ПРОЛОГ обусловлен скорее привычностью к какому-то языку, чем их достоинствам или недостаткам.

Логика предикатов.

Понятие предиката обычно связывают с логическим высказыванием, записываемым в форме К P(t₁,t_2,…,t_n); где К - квантор (обычно используется 2 квантора $ - существования и " - общности);

Р – предикатный символ для которого возможны 2 значения (1 – истина, и 0 – ложь); и t₁,t_2,…,t_n - термы, т.е. либо константы, либо переменные.

Из предикатов строятся логические формулы, причем правильно построенными формулами в логике предикатов первого порядка являются коньюктивные нормальные формы, т.е. формулы вида

дизъюнкты

где 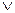- операция дизъюнкции;

& - логическая операция конъюнкции;

~ - прямое либо инверсное значение предиката.

Для определения истинности ППФ – правильно построенной формулы обычно используют метод резолюции, который заключается в поиске среди множества дизъюнктов хотя бы одного ложного. Для этого образуют из двух дизъюнктов, содержащих дополнительную пару, резольвенту, например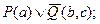

P(a) – резольвента

Q(b,c) – дополнительная пара

Нахождение хотя бы одного ложного дизъюнкта в ППФ означает ложность этой формулы, а доказательством истинности некоторого дизъюнкта будет являться нахождение пустой резольвенты для инверсии этого дизъюнкта (т.е. выполняется доказательство “от противного”).