Начинаем рассматривать собственно процесс вычисления двойного интеграла 
и знакомиться с его геометрическим смыслом.
Двойной интеграл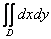 
численно равен площади плоской фигуры 
(области интегрирования). Это простейший вид двойного интеграла, когда функция двух переменных равна единице: 
.
Сначала рассмотрим задачу в общем виде. Сейчас вы немало удивитесь, насколько всё действительно просто! Вычислим площадь плоской фигуры , ограниченной линиями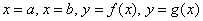 
. Для определённости считаем, что 
на отрезке 
. Площадь данной фигуры численно равна:
Изобразим область на чертеже:
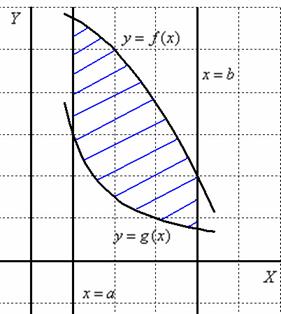
Выберем первый способ обхода области:
Таким образом: 
И сразу важный технический приём: повторные интегралы можно считать по отдельности. Сначала внутренний интеграл, затем – внешний интеграл. Данный способ настоятельно рекомендую начинающим в теме чайникам.
1) Вычислим внутренний интеграл, при этом интегрирование проводится по переменной «игрек»:
Неопределённый интеграл тут простейший, и далее используется банальная формула Ньютона-Лейбница, с той лишь разницей, что пределами интегрирования являются не числа, а функции. Сначала подставили в «игрек» (первообразную функцию) верхний предел, затем – нижний предел
2) Результат, полученный в первом пункте необходимо подставить во внешний интеграл:
Более компактная запись всего решения выглядит так:
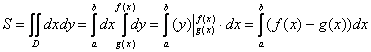
Полученная формула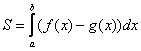 
– это в точности рабочая формула для вычисления площади плоской фигуры с помощью «обычного» определённого интеграла! Смотрите урок Вычисление площади с помощью определенного интеграла, там она на каждом шагу!
То есть, задача вычисления площади с помощью двойного интеграла мало чем отличается от задачи нахождения площади с помощью определённого интеграла! Фактически это одно и тоже!
Соответственно, никаких трудностей возникнуть не должно! Я рассмотрю не очень много примеров, так как вы, по сути, неоднократно сталкивались с данной задачей.
Пример 9
С помощью двойного интеграла, вычислить площадь плоской фигуры , ограниченной линиями 
, 
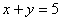
Решение: Изобразим область на чертеже:
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
Выберем следующий порядок обхода области:
Здесь и далее я не буду останавливаться на том, как выполнять обход области, поскольку в первом параграфе были приведены очень подробные разъяснения.
Таким образом:
Как я уже отмечал, начинающим лучше вычислять повторные интегралы по отдельности, этого же метода буду придерживаться и я:
1) Сначала с помощью формулы Ньютона-Лейбница разбираемся с внутренним интегралом:
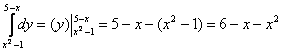
2) Результат, полученный на первом шаге, подставляем во внешний интеграл:
Пункт 2 – фактически нахождение площади плоской фигуры с помощью определённого интеграла.
Ответ: 
Вот такая вот глупая и наивная задача.
Любопытный пример для самостоятельного решения:
Пример 10
С помощью двойного интеграла, вычислить площадь плоской фигуры , ограниченной линиями 
, 
, 
Примерный образец чистового оформления решения в конце урока.
В Примерах 9-10 значительно выгоднее использовать первый способ обхода области, любознательные читатели, кстати, могут изменить порядок обхода и вычислить площади вторым способом. Если не допустите ошибку, то, естественно, получатся те же самые значения площадей.
Но в ряде случаев более эффективен второй способ обхода области, и в заключение курса молодого ботана рассмотрим ещё пару примеров на эту тему:
Пример 11
С помощью двойного интеграла, вычислить площадь плоской фигуры , ограниченной линиями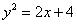 
, 
Решение: нас с нетерпением ждут две параболы, которые лежат на боку.
Как проще всего сделать чертёж?
Представим параболу 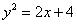в виде двух функций:
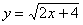– верхняя ветвь и 
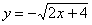– нижняя ветвь.
Аналогично, представим параболу в виде верхней 
и нижней 
ветвей.
Далее рулит поточечное построение графиков, в результате чего получается вот такая причудливая фигура:
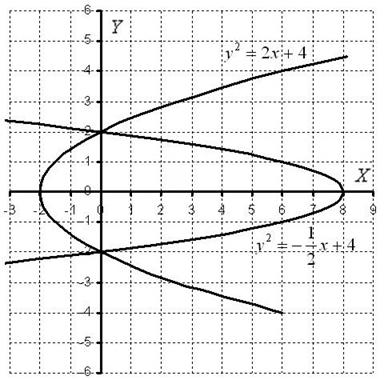
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
Что будет, если мы выберем первый способ обхода области? Во-первых, данную область придётся разделить на две части. А во-вторых, мы будем наблюдать сию печальную картину: 
. Интегралы, конечно, не сверхсложного уровня, но… существует старая математическая присказка: кто с корнями дружен, тому зачёт не нужен.
Поэтому из недоразумения, которое дано в условии, выразим обратные функции:
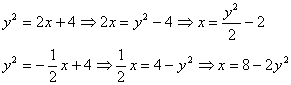
Обратные функции в данном примере обладают тем преимуществом, что задают сразу всю параболу целиком без всяких там листьев, желудей веток и корней.
Согласно второму способу, обход области будет следующим:
Таким образом:
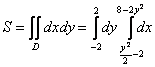
Как говорится, ощутите разницу.
1) Расправляемся с внутренним интегралом:
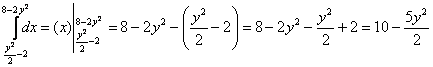
Результат подставляем во внешний интеграл:
2)
Интегрирование по переменной «игрек» не должно смущать, была бы буква «зю» – замечательно бы проинтегрировалось и по ней. Хотя кто прочитал второй параграф урока Как вычислить объем тела вращения, тот уже не испытывает ни малейшей неловкости с интегрированием по «игрек».
Также обратите внимание на первый шаг: подынтегральная функция 
является чётной, а отрезок интегрирования симметричен относительно нуля. Поэтому отрезок можно споловинить, а результат – удвоить. Данный приём подробно закомментирован на уроке Эффективные методы вычисления определённого интеграла.
Что добавить…. Всё!
Ответ: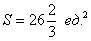 
Для проверки своей техники интегрирования можете попробовать вычислить . Ответ должен получиться точно таким же.