Классическое и статистическое определения вероятности
Случайные события
Событием называется результат некоторого испытания (опыта, наблюдения и т.п.).
Событие называется случайным по отношению к данному испытанию, если при осуществлении этого испытания оно может произойти, а может и не произойти.
Пример 1. Случайными являются события:
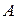– «при бросании игрального кубика выпало 2 очка»;
– «при бросании монеты появился герб»;
– «при выстреле стрелок попал в цель»
Событие называется достоверным, если оно обязательно произойдет при осуществлении данного испытания.
Событие называется невозможным, если оно не может произойти при осуществлении данного испытания.
Пример 2. Событие 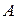– «при бросании игрального кубика выпало 7 очков» является невозможным, а событие – «при бросании игрального кубика выпало меньше 7 очков» является достоверным.
Вместо слова «произойдет» о событии часто говорят «появится», «наступит».
Два события называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании.
Пример 3. Брошена монета. События 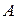– «появился герб» и – «появилась цифра» несовместны, так как при однократном бросании монеты появление герба исключает появление цифры.
Несколько событий называются несовместными, если они попарно несовместны.
Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании.
Пример 4. Монета брошена два раза. События 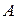– «появился герб при первом бросании» и – «появился герб при втором бросании» являются совместными.
Несколько событий образуют полную группу событий, если в результате испытания обязательно появится хотя бы одно из них.
События называются равновозможными, если по условию испытания нет оснований считать появление какого-либо из них более возможным, чем появление любого другого.
Классическое определение вероятности
Пусть события 
по отношению к некоторому испытанию: 1) образуют полную группу событий; 2) являются несовместными; 3) являются равновозможными. Такие события называются элементарными событиями для данного испытания или элементарными исходами данного испытания.
Элементарное событие 
называется благоприятствующим событию 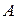, если появление события влечет за собой появление события .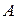
Вероятностью события 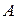называется отношение числа благоприятствующих этому событию элементарных исходов к общему числу всех элементарных исходов данного испытания.
Итак, вероятность события 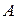определяется формулой:
, где
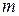– число элементарных исходов, благоприятствующих ;
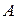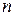– число всех возможных элементарных исходов испытания.
Из определения вероятности следует, что вероятность любого события 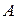удовлетворяет двойному неравенству: 
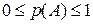. При этом вероятность достоверного события равна 1, а вероятность невозможного события равна 0.
Пример 5. Брошен игральный кубик. Найти вероятности следующих событий: 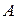– «выпало четное число очков», – «выпало 3 очка», – «выпало более 4 очков».
Рассмотрим события: 
– «выпало 1 очко», 
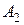– «выпало 2 очка», 
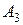– «выпало 3 очка», 
– «выпало 4 очка», 
– «выпало 5 очков», 
– «выпало 6 очков». Очевидно, что эти события равновозможны, несовместны и образуют полную группу событий. Следовательно, события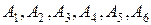 
являются элементарными исходами данного испытания (бросания игрального кубика). Таким образом, число всех элементарных исходов испытания 
.
Благоприятствующими событию 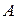являются три элементарных исхода – 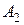, , . Следовательно, по определению вероятности, 
.
Событию благоприятствует только один элементарный исход 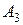, значит, 
.
Благоприятствующими событию являются два элементарных исхода – и . Следовательно, 
.