Рассмотрим в плоскости  материальную пластину, т.е. некоторую область
материальную пластину, т.е. некоторую область  , в которой распределено некое вещество с поверхностной плотностью
, в которой распределено некое вещество с поверхностной плотностью 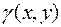 . Тогда, как известно (см. § 1, IV), масса всей пластины есть двойной интеграл по
. Тогда, как известно (см. § 1, IV), масса всей пластины есть двойной интеграл по  от
от 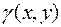 :
:

Один из примеров вычисления массы приведён в § 3. Рассмотрим ещё один характерный пример.
Пример Вычислить массу прямоугольного равнобедренного тре-угольника с гипотенузой  . Известно, что плотность
. Известно, что плотность  в любой точке
в любой точке  треугольника пропорциональна расстоянию от
треугольника пропорциональна расстоянию от  до гипотенузы, а в вершине прямого угла равна
до гипотенузы, а в вершине прямого угла равна  .
.

|
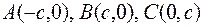 .
.
Уравнения катетов: 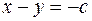 (левый) и
(левый) и
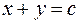 (правый). Таким образом, область можно записать так:
(правый). Таким образом, область можно записать так:

Рис.8
Лучше, однако, записать область иначе:

Далее, по условию 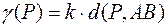 , т.е.
, т.е.  . Коэффициент пропорциональности находим из условия
. Коэффициент пропорциональности находим из условия

Итак, для искомой массы имеем:

Отметим, что размерность полученного ответа – это размерность массы.
Итак, для искомой массы имеем:
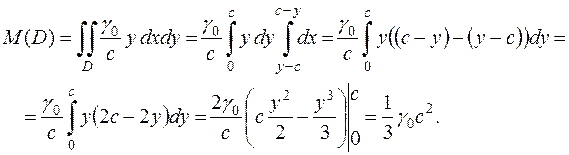
Отметим, что размерность полученного ответа – это размерность массы.
Вычисление координат центра масс пластины
Известно из физики, что, если масса распределена дискретно в отдельных 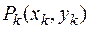 точках, то координаты
точках, то координаты  центра масс такой системы материальных точек вычисляются по формулам
центра масс такой системы материальных точек вычисляются по формулам

в которых  – масса, сосредоточенная в точке
– масса, сосредоточенная в точке  .
.
Пусть теперь в плоской области  имеем непрерывное распределение массы с поверхностной плотностью
имеем непрерывное распределение массы с поверхностной плотностью 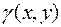 . Чтобы найти координаты центра масс такой области, поступим обычным образом. Разобьём область
. Чтобы найти координаты центра масс такой области, поступим обычным образом. Разобьём область  на отдельные части
на отдельные части  и выберем точки
и выберем точки  Масса
Масса  , распределенная в
, распределенная в 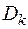 , приближенно равна
, приближенно равна  , где
, где  – площадь области
– площадь области 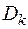 . Если считать, что вся масса
. Если считать, что вся масса  сосредоточена в точке
сосредоточена в точке  , то придём к дискретному распределению массы, и поэтому
, то придём к дискретному распределению массы, и поэтому

Чтобы получить точные значения для  и
и  , необходим переход к пределу при
, необходим переход к пределу при 
Но три суммы в написанных выше формулах – это интегральные суммы и в пределе дадут интегралы:

Интегралы, стоящие в числителях этих формул, называют статическими моментами области  относительно осей
относительно осей  и
и  соответственно.
соответственно.
Тройные интегралы
Повторный интеграл в пространстве вводится аналогично повторному интегралу на плоскости.
Пусть функция  непрерывна в правильной области
непрерывна в правильной области 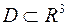 , причём
, причём 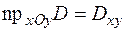 – правильная область в
– правильная область в 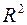 :
:


Зафиксируем точку  и проинтегрируем непрерывную функцию
и проинтегрируем непрерывную функцию 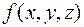 –функцию одной переменной
–функцию одной переменной  ! – по отрезку
! – по отрезку 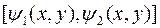 . Очевидно, что полученный интеграл будет зависеть от координат точки
. Очевидно, что полученный интеграл будет зависеть от координат точки  :
:

Можно показать, что функция  – непрерывная. Следовательно, существует повторный интеграл от этой функции по области
– непрерывная. Следовательно, существует повторный интеграл от этой функции по области  :
:

или, окончательно,
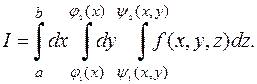 (3)
(3)
Эта конструкция и называется повторным интегралом в  . Ещё раз заметим, что вычисление такого интеграла производится справа налево! Избегайте грубых ошибок: в пределах интегрирования внутренних интегралов могут быть только внешние переменные.
. Ещё раз заметим, что вычисление такого интеграла производится справа налево! Избегайте грубых ошибок: в пределах интегрирования внутренних интегралов могут быть только внешние переменные.
Очевидно, что кроме рассмотренного порядка интегрирования (сначала по  , потом по
, потом по  и, наконец, по
и, наконец, по  ) существуют и другие порядки, причём все они приводят к одному и тому же числу
) существуют и другие порядки, причём все они приводят к одному и тому же числу 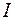 .
.
Пример. Расставить пределы интегрирования в повторном интеграле от функции  по области
по области  ограниченной поверхностями
ограниченной поверхностями  ,
, 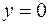 ,
,  ,
,  .
.
Решение. Все указанные поверхности – это плоскости:  и
и 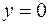 – координатные,
– координатные,  – параллельна координатной
– параллельна координатной  . Вместе с четвёртой плоскостью они ограничивают некий тетраэдр. Его проекция на
. Вместе с четвёртой плоскостью они ограничивают некий тетраэдр. Его проекция на 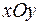 – это треугольник ограниченный осями
– это треугольник ограниченный осями  ,
, 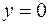 и прямой, которая является проекцией линии пересечения граней
и прямой, которая является проекцией линии пересечения граней  и
и  . Исключая переменную
. Исключая переменную  из этих уравнений, получим уравнение проекции:
из этих уравнений, получим уравнение проекции: 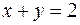 .
.

Рис.9
Итак, для точек области  имеем: 1) абсцисса
имеем: 1) абсцисса  изменяется от 0 до 2; 2) для каждого фиксированного
изменяется от 0 до 2; 2) для каждого фиксированного  ордината
ордината  изменяется от 0 до прямой
изменяется от 0 до прямой 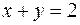 , т.е. до
, т.е. до 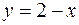 ; 3) аппликата
; 3) аппликата  изменяется от плоскости
изменяется от плоскости  до плоскости
до плоскости  , т.е. до
, т.е. до  . Стандартная запись области:
. Стандартная запись области:

Повторный интеграл имеет вид:
 .
.
Ещё раз напомним: вычисления производятся справа налево!
Криволинейные интегралы
Криволинейный интеграл 1 - го рода. Пусть функция f(x,y) определена и непрерывна в точках дуги АВ гладкой кривой L. Разобьём дугу АВ произвольным образом на n элементарных дуг точками А = А0, А1,…,Аn = В, имеющих длину ∆σ  , ∆σ
, ∆σ  , …, ∆σ
, …, ∆σ  . Выберем на каждой элементарной дуге произвольную точку P
. Выберем на каждой элементарной дуге произвольную точку P  (ξ
(ξ  ;ηк) и умножим значение функции в точки P
;ηк) и умножим значение функции в точки P  на длину соответствующей дуги.
на длину соответствующей дуги.
Интегральной суммой для функции f(x,y) по длине дуги АВ называется сумма вида
 .
.
Если при max s 
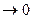 интегральная сумма имеет определенный конечный предел
интегральная сумма имеет определенный конечный предел
I = 
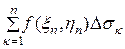 ,
,
то этот предел называется криволинейным интегралом по длине дуги АВ от функции f(x, y) и обозначается следующим образом:
 .
.
Если кривая задана уравнением у = j(х) (а £ х £ в), то

 .
.
Если кривая задана параметрическими уравнениями х = х(t), y = y(t) (a£ t £ b), то

 .
.
Основные свойства криволинейного интеграла 1 - го рода:
1. Криволинейный интеграл 1 - го рода не зависит от направления пути интегрирования: 
 .
.
2. 
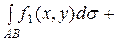
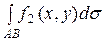 .
.
3.  к
к  , где к - константа.
, где к - константа.
4. Если К = К1ÈК2, то 

 .
.
Пример. Вычислить интеграл  , где L - дуга параболы
, где L - дуга параболы
у2 = 2х от точки (0,0) до точки (4,2  ).
).
Решение. Здесь линию удобно задать в форме, разрешенной относительно х: х =  . Тогда х¢ = у и интеграл преобразуется к виду
. Тогда х¢ = у и интеграл преобразуется к виду  =
= 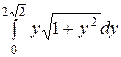 =
=  .
.
Криволинейный интеграл 2 - го рода. Пусть функции Р(х,у) и Q(x,y) непрерывны в точках дуги АВ гладкой кривой АВ. Интегральной суммой для функций Р(х,у) и Q(x,y) по координатам называется сумма вида
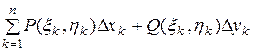 ,
,
где Dк и Dк - проекции дуги на оси Ох и Оу.
Криволинейным интегралом по координатам от выражения Р(х,у)dx+ +Q(x,y)dy по направленной дуге АВ называется предел интегральной суммы при условии, что max Dх 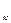
 и max Dу
и max Dу 
 :
:

 .
.
Если кривая задана уравнением у = j(х) (а £ х £ в), то

 .
.
Если кривая задана параметрическими уравнениями х = х(t), y = y(t) (a£ t £ b), то

 .
.
Основные свойства криволинейного интеграла 2 - го рода. Криволинейный интеграл 2 - го рода меняет знак на противоположный при изменении направления пути интегрирования:

 .
.
Остальные свойства аналогичны свойствам интеграла 1 - го рода.
Пример Вычислить интеграл  , принимая за линию L:
, принимая за линию L:
1) отрезок прямой, соединяющий точки О (0,0) и А(1,1);
2) дугу параболы у = х2, соединяющей эти же точки.
Решение:
1. Уравнение линии интегрирования у = х. Следовательно, dy = dx и  =
= 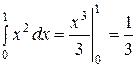 .
.
2. у = х2, dy = 2xdx и  =
=  =
= 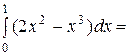
 =
=
 .
.
Криволинейные интегралы по замкнутому множеству обозначим символом  В случае замкнутого контура на плоскости направление обхода, при котором область, ограниченная контуром, остается слева (обход контура совершается против хода часовой стрелки), называется положительным.
В случае замкнутого контура на плоскости направление обхода, при котором область, ограниченная контуром, остается слева (обход контура совершается против хода часовой стрелки), называется положительным.
Формула Грина. Если функции Р(х,у) и Q(х,у) непрерывны вместе со своими частными производными первого порядка в области Д, то имеет место формула
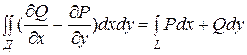 ,
,
где L - граница области Д, и интегрирование вдоль L производится в положительном направлении.
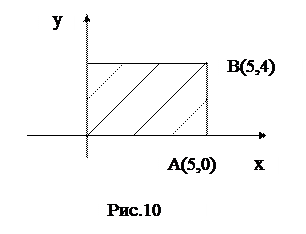 Пример 7. Применяя формулу Грина, вычислить интеграл
Пример 7. Применяя формулу Грина, вычислить интеграл  , где L - контур прямоугольника с вершинами
, где L - контур прямоугольника с вершинами
О (0,0), А(5,0), В(5,4) и С(0,4).
Решение. Так как Р(х,у) = х2+у2, Q(x,y) = (х+у)2, то  . Таким образом
. Таким образом 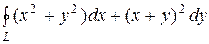 = =
= =  = I, Д - область прямоугольника ОАВС (рис.17).
= I, Д - область прямоугольника ОАВС (рис.17).
Вычислим двойной интеграл по данной области Д:
Д=  . I=
. I= 
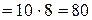 .
.