КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
ПЛАН ЛЕКЦИИ
I. Криволинейный интеграл второго рода (по координатам).
II. Вычисление криволинейного интеграла второго рода.
III. Формула Грина.
IV. Условие независимости криволинейного интеграла от пути интегрирования.
V. Криволинейный интеграл первого рода (по длине дуги).
I. Криволинейный интеграл второго рода (по координатам). Пусть точка 
движется по плоской линии 
от точки 
к точке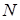 
под действием силы 
, меняющейся по величине и направлению при перемещении точки 
.
Вычислим работу A силы при перемещении точки P из положения M в положение N. Для этого разобьем кривую MN на n произвольных частей точками 
, 
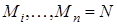в направлении от M к N и обозначим через 
вектор 
. Величину силы в точке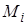 
обозначим 
.
Работа силы 
вдоль дуги 
приближенно равна 
. При этом считаем, что сила постоянна при перемещении из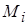 
в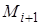 
, и криволинейный путь заменяем вектором . Пусть 
, где 
и 
- проекции вектора на оси Ox и Oy соответственно. Вектор 
. Тогда 
.
Приближенное значение работы A силы на всей кривой MN можно найти как сумму
. (1)
Переходя к пределу интегральной суммы (1) при 
, получим точное выражение для работы A силы :
. (2)
Предел, стоящий в правой части равенства (2), называют криволинейным интегралом второго рода от и по кривой L и обозначают
(3)
Свойства криволинейного интеграла второго рода:
1) криволинейный интеграл определяется подынтегральным выражением, формой кривой интегрирования и указанием направления интегрирования, причем
;
2) если кривую L разбить на две части точкой K, так что 
, то
Если кривая L замкнута, то есть точки M и N совпадают, то криволинейный интеграл по замкнутому контуру обозначают 
.
II. Вычисление криволинейного интеграла второго рода. Пусть кривая L задана уравнением в параметрической форме 
, 
. Тогда 
, 
. Если точке M кривой L соответствует значение параметра 
, а точке N соответствует значение 
, то от криволинейного интеграла (3) можно перейти к определенному интегралу:
Если в качестве параметра t взять координату x, т.е. положить 
, 
, 
, то
Если в качестве параметра t принять координату у, т.е. положить 
, 
, 
, то
Пример 1. Вычислить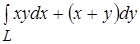 
, где L - четверть окружности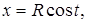 
от 
до 
Решение. Найдем 
, тогда
Пример 2. Вычислить 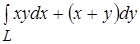, где
1) линия L - парабола 
от точки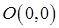 
до точки 
;
2) линия L - двухзвенная ломаная, стороны которой параллельны осям координат.
Решение.
Случай (1): , 
;
Случай (2): 
на отрезке 
: 
; 
, 
,
;
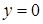на отрезке 
: 
, 
, 
, 
,
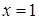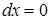тогда 
.
Случай (3):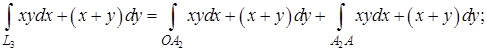 
на отрезке 
: 
, , 
, 
,
;
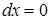на отрезке 
: 
, , 
, 
,
,
тогда 
.
С помощью криволинейного интеграла второго рода можно вычислить площадь, ограниченную замкнутой линией L по формуле: 
.
Пример. Вычислить площадь эллипса, заданного уравнениями в параметрической форме: 
, 
.
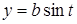Решение. 
III. Формула Грина. Установим связь между двойным интегралом по некоторой плоской области D и криволинейным интегралом по границе L этой области. Пусть в плоскости Oxy задана область D, правильная в отношении осей Ox и Oy и ограниченная снизу кривой 
, а сверху кривой 
, 
. В совокупности обе эти кривые составляют замкнутый контур L.
Пусть в области D заданы две непрерывные функци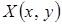и 
и 
, имеющие непрерывные частные производные.
Рассмотрим интеграл
Представляя его в виде двукратного, получим
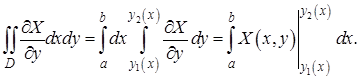
Заметим, что
Тогда
(4)
Аналогично найдем
(5)
Вычитая из (4) выражение (5), получим
,
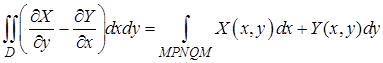или
, (6)
где обход контура L совершается против часовой стрелки.
Формула (6) носит название формулы Грина.
IV. Условие независимости криволинейного интеграла от пути интегрирования. Рассмотрим две произвольные кривые MPN и MQN, лежащие в некоторой плоской области D и соединяющие точки M и N.
Пусть криволинейный интеграл второго рода не зависит от формы кривой интегрирования, а зависит только от положения начальной и конечной точек M и N. В этом случае
.
Тогда
Меняя направление интегрирования во втором интеграле, получим
то есть криволинейный интеграл по замкнутому контуру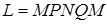 
равен нулю:
.
Таким образом, из условия независимости криволинейного интеграла от формы кривой интегрирования следует равенство нулю криволинейного интеграла по любому замкнутому контуру, лежащему в области D. Справедливо и обратное утверждение: если в области D криволинейный интеграл по любому замкнутому контуру равен нулю, то этот интеграл не зависит от формы кривой, соединяющей любые две точки, а зависит только от положения этих точек.
Для того чтобы криволинейный интеграл по любому замкнутому контуру был равен нулю, необходимо и достаточно, чтобы выполнялось равенство
. (7)
Доказательство этого утверждения основывается на рассмотрении формулы Грина. Если условие (7) выполняется, то левая часть равенства (6) равна нулю и
.
Выполнение условия (7) равносильно тому, что выражение 
есть полный дифференциал некоторой функции 
, то есть 
, причем 
. В этом случае
, 
то есть криволинейный интеграл по любой кривой 
, соединяющей точки M и N, равняется разности значений функции в этих точках.
V. Криволинейный интеграл первого рода (по длине дуги). Пусть функция 
непрерывна в некоторой области D и L – линия, целиком расположенная в этой области. Разобьем кривую L на n участков; возьмем на каждом участке произвольную точку 
и построим интегральную сумму
, (8)
где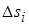 
– длина соответствующего участка линии L.
Криволинейным интегралом по длине дуги (первого рода) называется предел n -й интегральной суммы (8) при условии, что длина наибольшего из участков разбиения стремится к нулю:
.
Вычисление криволинейного интеграла первого рода осуществляется путем сведения его к определенному интегралу исходя из того, что 
Если линия L задана параметрическими уравнениями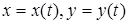 
, то
.
Если линия L задана уравнением 
, то
.
Если линия L задана уравнением 
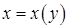, то
.
К понятию криволинейного интеграла первого рода приводит задача об отыскании массы кривой. Если плотность линии задана функцией 
, то масса линии 
определяется интегралом 
. Длина линии может быть вычислена с помощью криволинейного интеграла 
.
Пример. Найти массу дуги окружности 
, расположенной в первом октанте, если плотность определяется функцией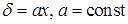 
.
Решение. Запишем функцию плотности в параметрической форме 
, тогда
