ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ................................................................................................. 4
ВЫЧИСЛЕНИЕ ДРОБНОЙ СТЕПЕНИ КОМПЛЕКСНОГО ЧИСЛА 4
ПОСТРОЕНИЕ ГОДОГРАФА КОМПЛЕКСНОЙ ФУНКЦИИ........... 5
3. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
С ИСПОЛЬЗОВАНИЕМ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ........... 6
4. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
КЛАССИЧЕСКИМ СПОСОБОМ.............................................................. 7
ОФОРМЛЕНИЕ...................................................................................... 7
БИБЛИОГРАФИЧЕСКИЙ СПИСОК....................................................... 8
ПРИЛОЖЕНИЕ. Варианты заданий расчетной работы.............. 9
ВВЕДЕНИЕ
Расчетная работа проводится по первому разделу дисциплины «Основы теории управления» и предусматривает выполнение следующих вычислений, позволяющих студентам восстановить свои знания и умения по разделам математики, используемым в данной дисциплине:
1) расчет и изображение на плоскости дробной степени комплексного числа;
2) расчет и изображение на комплексной плоскости годографа комплексной функции;
3) решение дифференциального уравнения с использованием операционного исчисления;
4) решение дифференциального уравнения классическим способом.
Каждый студент получает индивидуальный вариант задания (приведены в приложении) и выполняет его в установленный срок – 2 недели.
ВЫЧИСЛЕНИЕ ДРОБНОЙ СТЕПЕНИ КОМПЛЕКСНОГО ЧИСЛА
Предлагается вычислить и изобразить на плоскости все числа
 .
.
Удобно использовать показательную форму комплексного числа
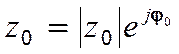 ,
,
где j0 – аргумент z 0.
При определении j0 лучше всего изобразить это число в виде вектора и использовать полное значение аргумента в пределах 0-2p, а не только главное значение, которое дают стандартные тригонометрические функции.
Затем определяется целая степень (положительная или отрицательная) числа z 0 , которая дает одно число:
 .
.
На последнем этапе определяется корень n -й степени, который дает n значений:
 ,
,
где j1 – аргумент z1.
Все n чисел должны быть показаны в виде векторов на комплексной плоскости.
ПОСТРОЕНИЕ ГОДОГРАФА КОМПЛЕКСНОЙ ФУНКЦИИ
Предлагается изобразить график комплекснозначной функции вещественного аргумента w на комплексной плоскости при изменении этого аргумента от 0 до ¥. Такой график называют годографом функции, который представляет траекторию конца вектора комплексной функции при изменении параметра wÎ[0,¥). График должен иметь качественный вид, отражать начало, примерное прохождение и окончание функции.
Функции являются дробно-рациональными. Удобно представить их в виде произведения более простых функций и в показательной форме. Построить годографы этих составляющих, а затем объединить их в итоговый годограф, учитывая, что при умножении модули также перемножаются, а аргументы складываются.
Поясним на небольшом примере
 .
.
Годограф первой функции на комплексной плоскости выглядит как прямая линия, начинающаяся в точке 2 на вещественной оси и уходящая вертикально вверх.

Годограф второй составляющей строится в два этапа: сначала один знаменатель (jw-1), что дает аналогичный годограф, только начинающийся из точки –1, затем берем обратную функцию, что при показательном представлении означает следующее: модуль будет обратным и меняться от 1 до 0 (у знаменателя от 1 до ¥), а у аргумента будет меняться знак от –180° до –90° (у знаменателя от 180 до 90). Таким образом, годограф z 2 представляет полуокружность.

Объединяем z 1 и z 2 : модули перемножаем, фазы складываем, получаем полуокружность с начальным модулем 2, фазой –180°, и конечным модулем 1, фазой 0°. Угол меняется против часовой стрелки. Здесь же покажем и z 3: сначала jw – годограф проходит по мнимой оси в положительном направлении, а затем обратную, так как z 3 = 1/ jw: модуль меняется от ¥ до 0, а фаза постоянна и равна -90°.

На последнем этапе объединяем z 1 z 2 и z 3: можно z 1 z 2 повернуть на -90°, начальный модуль устремить к ¥, фаза -270°, конечный модуль будет равен 0, а фаза -90°. Качественный вид итогового годографа показан ниже.

3. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
С ИСПОЛЬЗОВАНИЕМ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
Основным достоинством операционного исчисления является возможность алгебраизации дифференциальных уравнений. Это означает, что после перехода в область изображений используются только алгебраические операции и находится изображение решения дифференциального уравнения, при этом автоматически учитываются начальные условия. Таким образом, решение дифференциального уравнения разбивается на два этапа: получение изображения решения и определение оригинала по изображению.
На первом этапе при алгебраизации дифференциального уравнения пользуются стандартными формулами:

Здесь через L обозначено применение к функции преобразования Лапласа, т.е. переход к изображению. Изображение функции в правой части дифференциального уравнения можно найти по таблицам, которые есть как в учебной литературе по математике, так и в литературе по теории управления [1-6].
На втором этапе определения оригинала по изображению в случае дробно-рациональной функции можно воспользоваться формулой на основе вычетов:
 .
.
В этой формуле l -количество различных полюсов функции Y(s), ki – кратность i –го полюса.
Другим способом является разложение изображения на простые слагаемые и нахождение по таблице оригинала каждого слагаемого. В случае вещественных кратных полюсов количество слагаемых равно кратности полюса, каждое слагаемое в знаменателе имеет сомножитель
 .
.
В случае комплексных полюсов слагаемое должно быть приведено к табличному виду с помощью выделения полного квадрата:
 .
.
Далее остается разложить на два слагаемых, чтобы в числителе были табличные выражения.