СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ
Пусть при x → a функции f(x) и g(x) являются бесконечно малыми. Тогда будем пользоваться следующими определениями.
1. Если  , то f(x) называется бесконечно малой высшего порядка, чем g(x) (относительно g(x)).
, то f(x) называется бесконечно малой высшего порядка, чем g(x) (относительно g(x)).
2. Если  , то функции f(x) и g(x) называются бесконечно малыми одногопорядка.
, то функции f(x) и g(x) называются бесконечно малыми одногопорядка.
3. Если  , то f(x) называется бесконечно малой k-го порядка относительноg(x).
, то f(x) называется бесконечно малой k-го порядка относительноg(x).
Если  , то функции f(x) и g(x) называются эквивалентными бесконечно малыми. В этом случае обе функции стремятся к нулю примерно с одинаковой скоростью. Эквивалентные бесконечно малые будем обозначать f ≈ g.
, то функции f(x) и g(x) называются эквивалентными бесконечно малыми. В этом случае обе функции стремятся к нулю примерно с одинаковой скоростью. Эквивалентные бесконечно малые будем обозначать f ≈ g.
5. Таблица эквивалентно малых функций, с доказательством каждой из них. Поскольку в этой таблице мы всегда будем рассматривать базу  , для простоты записи обозначение этой базы будем пропускать и писать знак
, для простоты записи обозначение этой базы будем пропускать и писать знак  вместо
вместо  .!1)
.!1)  . Эту формулу мы уже доказали и использовали в примерах. Эквивалентность sinx и x при
. Эту формулу мы уже доказали и использовали в примерах. Эквивалентность sinx и x при  означает в точности, что первый замечательный предел равен 1.
означает в точности, что первый замечательный предел равен 1.
!2)  . Эта эквивалентность тоже была доказана выше в одном из примеров.
. Эта эквивалентность тоже была доказана выше в одном из примеров.
3)  . Докажем эту эквивалентность:
. Докажем эту эквивалентность:

!4)  . Докажите это в качестве упражнения, сделав замену
. Докажите это в качестве упражнения, сделав замену  и применив предыдущую табличную формулу.
и применив предыдущую табличную формулу.
!5  ). Для доказательства воспользуемся формулой
). Для доказательства воспользуемся формулой  . Далее, имеем:
. Далее, имеем:

Это означает, что доказываемая эквивалентность имеет место.
6)  . Для доказательства этой эквивалентности сделаем такое преобразование:
. Для доказательства этой эквивалентности сделаем такое преобразование:

Для вычисления предела правой части воспользуемся непрерывностью логарифма и вторым замечательным пределом:

и мы доказали формулу 6.
В частном случае, при a=e, получаем эквивалентность
6) 
7)  (). Для доказательства сделаем замену
(). Для доказательства сделаем замену  и выразим x через z:
и выразим x через z:  .Согласно формуле 6, при
.Согласно формуле 6, при  , откуда
, откуда  . Из непрерывности логарифма следует, что
. Из непрерывности логарифма следует, что  и, значит,
и, значит,  при
при  . В этой формуле осталось лишь сменить обозначение переменного z на x, чтобы получить формулу 7.
. В этой формуле осталось лишь сменить обозначение переменного z на x, чтобы получить формулу 7.
В частном случае, при a=e, получаем эквивалентность
!7) 
Сведём теперь полученные формулы в итоговую таблицу. Всюду в ней. 1).
| sin α(x) ~ α(x) 1 − cos α(x) ~ α(x)2/2 |
| tg α(x) ~ α(x) arcsin α(x) ~ α(x) |
| arctg α(x) ~ α(x) eA(X) − 1 ~ α(x) |
| a A(X) − 1 ~ α(x) · ln a ln[1 + α(x)] ~ α(x) |
| LOG a[1 + α(x)] ~ α(x)/ln a |
| [1 + α(x)]M − 1 ~ mα(x |
Непрерывность функции в точке
Пусть функция f (x) определена в некоторой окрестности O (x 0) точки x 0 (включая саму точку x 0). Функция f (x) называется непрерывной в точке x 0, если существует lim x → x 0 f (x), равный значению функции f (x) в этой точке:
f (x) = f (x 0),
|
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке Существуют левосторонний предел и правосторонний предел  ; Эти односторонние пределы конечны.
; Эти односторонние пределы конечны.
При этом возможно следующие два случая: Левосторонний предел и правосторонний предел равны друг другу:  Такая точка называется точкой устранимого разрыва. Левосторонний предел и правосторонний предел не равны друг другу:
Такая точка называется точкой устранимого разрыва. Левосторонний предел и правосторонний предел не равны друг другу:  Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов
Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов  называется скачком функции.
называется скачком функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
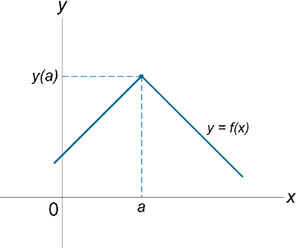
| Непрерывна при x = a. | Имеет разрыв при x = a. | |
| ||
| Непрерывна при x = a. | Имеет разрыв при x = a. |

 (*)Логарифмическую производную используют, например, при дифференцировании (нахождении производной или дифференциала) степенно-показательной функции
(*)Логарифмическую производную используют, например, при дифференцировании (нахождении производной или дифференциала) степенно-показательной функции - дифференцируемая функция от аргумента x в некотором интервале
- дифференцируемая функция от аргумента x в некотором интервале  . Если в уравнении
. Если в уравнении  , где
, где  - функция обратная данной.
- функция обратная данной.

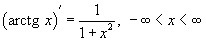





 точка
точка 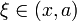 при x < a или
при x < a или  при x > a:
при x > a: