Определение 1. Точка  называется точкой локального максимума (минимума), а значение функции в ней – локальным максимумом (локальным минимумом) функции
называется точкой локального максимума (минимума), а значение функции в ней – локальным максимумом (локальным минимумом) функции  , если существует
, если существует  -окрестность
-окрестность  точки
точки  такая, что в любой точке
такая, что в любой точке  имеем
имеем  (соответственно,
(соответственно,  ).
).
Определение 2. Точка  называется точкой строгого локального максимума (минимума), а значение функции в ней – строгим локальным максимумом (локальным минимумом) функции
называется точкой строгого локального максимума (минимума), а значение функции в ней – строгим локальным максимумом (локальным минимумом) функции  , если существует
, если существует  -окрестность
-окрестность  точки
точки  такая, что в любой точке
такая, что в любой точке  имеем
имеем  (соответственно,
(соответственно,  ).
).

|

|

|

|

|

|

|

|

|

|

|

|
| Рис. 1.1 |
Определение 3. Точки локального максимума и минимума называются точками локального экстремума, а значения функции в них – локальными экстремумами функции.
Теорема 1. (необходимое условие локального экстремума функции). Если функция  дифференцируема в точке
дифференцируема в точке  и имеет в этой точке локальный экстремум, то
и имеет в этой точке локальный экстремум, то  .
.
Доказательство. По условию теоремы существует конечная производная  . Так как функция
. Так как функция  имеет в точке
имеет в точке  локальный экстремум, то она не может в этой точке
локальный экстремум, то она не может в этой точке  ни возрастать, ни убывать. Значит, производная
ни возрастать, ни убывать. Значит, производная  не может быть ни положительной, ни отрицательной. Тем самым доказано, что
не может быть ни положительной, ни отрицательной. Тем самым доказано, что 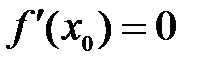 . ■
. ■
Теорема 1 имеет очень простой геометрический смысл: она утверждает, что если в той точке кривой  , в которой достигается локальный экстремум, существует касательная к этой кривой, то эта касательная обязательно параллельна оси Ох
, в которой достигается локальный экстремум, существует касательная к этой кривой, то эта касательная обязательно параллельна оси Ох
Определение 4. Точки, которых производная  функции
функции  обращается в нуль, называются стационарными точками функции
обращается в нуль, называются стационарными точками функции 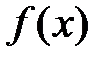
|

|

|
| касательная |

|
|

|

|
 и
и  ).
).
Определение 5. Точки, которых производная  функции
функции  не существует, но
не существует, но 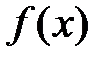 в них определена, называются критическими точками функции
в них определена, называются критическими точками функции 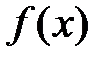







Нахождение асимптот графика функции одной переменной.
Определение 11 (вертикальная асимптота). Прямая x = a называется вертикальной асимптотой графика функции y = f(x), если хотя бы один из пределов
limx® a+0f(x) или limx® a-0f(x)
равен +Ґ или -Ґ.
Пример 14. График функции y = 1/(x-2) имеет вертикальную асимптоту x = 2, так как limx® 2+01/(x-2) = +Ґ, limx® 2-01/(x-2) = -Ґ (рис.28).

Определение 12 (наклонная асимптота). Говорят, что прямая y = kx+b является наклонной асимптотой графика функции y = f(x) при x® +Ґ, если f(x) имеет вид
f(x) = kx+b+a (x),
где limx® +Ґa (x) = 0.
Справедлива
Теорема 13 (существование асимптот). Для того чтобы график функции y = f(x) имел при x® +Ґ асимптоту y = kx+b, необходимо и достаточно, чтобы существовали два предела
limx® +Ґf(x)/x = k, limx® +Ґ(f(x)-kx) = b.
Доказательство.
Необходимость. Пусть график функции y = f(x) имеет при x® +Ґ асимптоту y = kx+b, то есть для f(x) имеет вид
f(x) = kx+b+a(x),
тогда
limx® +Ґf(x)/x = (kx+b+a(x))/x = k,
limx® +Ґ(f(x)-kx) = limx® +Ґ(b+a(x)) = b.
Достаточность. Пусть существуют пределы, фигурирующие в условии теоремы. Тогда величина f(x)-kx-b является бесконечно малой при x® +Ґ. Обозначив f(x)-kx-b = a(x) получим, что f(x) имеет асимптоту согласно определению наклонной асимптоты.
Замечание. Аналогично определяется наклонная асимптота и доказывается теорема 13 при x® -Ґ.
Замечание. Если k=0 в определении наклонной асимптоты, то наклонная асимптота является горизонтальной.