Теорема 1. (критерий сходимости ряда с неотрицательными членами)
Если 
ϵ N 
, то для сходимости ряда 
необходимо и достаточно, чтобы последовательность его частичных сумм 
была ограничена сверху, т.е. 
: ϵ N t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>k</m:t></m:r></m:sub></m:sSub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>≤M</m:t></m:r></m:e></m:nary></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
.
Заметим, что 
возрастающая последовательность, т.к. 
. Осталось воспользоваться теоремой о возрастающей последовательности.
Теорема 2. (интегральный признак сходимости ряда).
Если функция 
неотрицательная и убывает на 
, то ряд 
и интеграл 
сходятся или расходятся одновременно.
Обозначим 
, 
ϵ N 
. Т.к. убывает при 
, то она интегрируема на 
и ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
ϵ 
выполняется:
. Тогда 
. Просуммируем эти неравенства для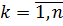 
, получим 
или 
.
a) Если интеграл сходится, то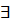 
, причем, т.к. 
, то 
, тогда 
, т.е. ограничена сверху. По Т1, ряд сходится.
б) Если ряд сходится, то 
(т.к.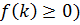 
. Тогда 
ϵ N т.к. 
, то последовательность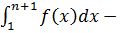 
возрастает. И т.к. она ограничена сверху, то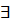 , т.е. интеграл сходится.
Теорема. (признак сравнения)
Если 
ϵ N 
, то из сходимости ряда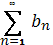 
следует сходимость 
а из расходимости следует расходимость .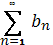
Следствие. Если 
и s w:val="28"/></w:rPr><m:t>n</m:t></m:r></m:sub></m:sSub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>>0</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
для ϵ N и 
при 
(т.е. 
= 1), то ряды и 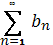сходятся или расходятся одновременно.
Теорема. (признак Даламбера)
Пусть дан ряд , где ϵ N. Тогда:
1) Если 
ϵ (0) и номер 
: 
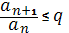, то ряд 
сходится.
2) Если 
ϵ N: 
, то ряд расходится.
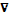a) По условию, s New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в?™q</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
, 
,…, 
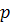ϵ N.
Т.к.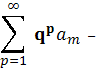 
сходится (см. пример ранее), то сходится ряд 
А значит сходится ряд , полученный добавлением к последнему 
.
б) Из условия следует, что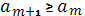 
, 
, 
и так далее. Значит, 
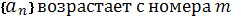, причем 
. Тогда 
. Значит, ряд расходится.
Следствие. (признак Даламбера в предельной форме).
Если 
, то ряд сходится при 
.
Замечание. При 
признак не дает ответа. Действительно, 
и 
…
Теорема. (признак Коши).
Пусть дан ряд , где 
ϵ N. Тогда:
1)Если 
(0;1) и номер 
, то ряд сходится.
2) Если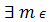 
N 
, то ряд расходится.
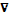a) Из условия следует, что 
, где 0 
. Из сходимости 
следует сходимость 
следовательно (по 2 свойству сходимости рядов).
б) Если , то 
следовательно s w:val="28"/></w:rPr><m:t>n</m:t></m:r></m:sub></m:sSub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>↛0.</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
Ряд расходится.
Следствие. (признак Коши в предельной форме).
Если 
, то при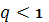 
ряд сходится, а при 
ряд расходится.
При признак не дает ответа.
Если интеграл расходится, то и ряд расходится (от противного: если бы ряд сходился, то по ранее доказанному и интеграл то же бы сходился). Аналогично из расходимости ряда следует расходимость интеграла.