Если f – суммируемая функция и при фиксированном х и некотором  интеграл
интеграл 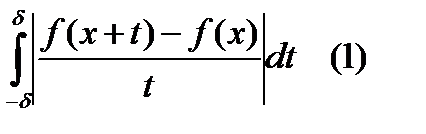
существует, то частичные суммы Sn ряда Фурье функции f сходятся в этой точке х к f(x).
Достаточное условие сходимости ряда Фурье.
Если f – суммируемая функция и при фиксированном х и некотором существует, то частичные суммы Sn ряда Фурье функции f сходятся в этой точке х к f(x). |
11. Ряд Фурье для функций с периодом 2π, для функций с произвольным периодом. Тригонометрический ряд Фурье в комплексной форме.
Ряд Фурье функции с произвольным периодом
Предположим, что функция f задана в промежутке [-l,l], где l -- некоторое положительное число. Сделав подстановку
 получим функцию
получим функцию  ,определенную в промежутке ,определенную в промежутке 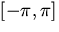 .Функции g соответствует (формальный) ряд Фурье .Функции g соответствует (формальный) ряд Фурье
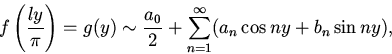 коэффициенты которого находятся по формулам Эйлера -- Фурье:
коэффициенты которого находятся по формулам Эйлера -- Фурье:

 Возвращаясь к старой переменной, т.е. полагая в выписанных формулах
Возвращаясь к старой переменной, т.е. полагая в выписанных формулах  ,мы получим для функции f тригонометрический ряд несколько измененного вида: ,мы получим для функции f тригонометрический ряд несколько измененного вида:

|
где

 Ряд Фурье для функций с периодом 2π
Периодическая функция f (x) с периодом T = 2π допускает представление в виде ряда Фурье
Ряд Фурье для функций с периодом 2π
Периодическая функция f (x) с периодом T = 2π допускает представление в виде ряда Фурье
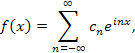 коэффициентыкоторого определяются формулой
коэффициентыкоторого определяются формулой
 Выражение
Выражение  называется комплексной формой ряда Фурье функции f(x), если называется комплексной формой ряда Фурье функции f(x), если  определяется равенством определяется равенством  где
где  Переход от ряда Фурье в комплексной форме к ряду в действительной форме и обратно осуществляется с помощью формул:
Переход от ряда Фурье в комплексной форме к ряду в действительной форме и обратно осуществляется с помощью формул:
|
Косинус- и синус- преобразование Фурье и их свойства.
Косинус-преобразование функции f
 Cинус-преобразование функции f
Cинус-преобразование функции f
 Комплексная форма интеграла Фурье.
Интеграл Фурье в комплексной форме
Комплексная форма интеграла Фурье.
Интеграл Фурье в комплексной форме
 или
или

|
12. Интеграл Фурье. Косинус- и синус- преобразование Фурье и их свойства. Комплексная форма интеграла Фурье.
Интеграл Фурье
Интеграл Фурье для кусочно-непрерывной и абсолютно интегрируемой на  функции f: функции f:
 где
где
 Если f чётная, то
Если f чётная, то  интеграл Фурье
интеграл Фурье  Если f нечётная, то
Если f нечётная, то  интеграл Фурье
интеграл Фурье 
|
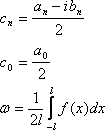 (n=1,2,...)
(n=1,2,...)
|
| 13. Основные понятия теории дифференциальных уравнений. Общее и частное решения. Соотношение, связывающее неизвестную функцию, независимые переменные и производные по этим переменным называют дифференциальными уравнениями(ДУ). Если неизвестная функция зависит только от первой переменной то уравнение называют обыкновенным диф. уравнением(ОДУ). Если же зависит от нескольких переменных называютДУ частных производных. Наивысший порядок производной входящей в уравнение называют порядком этого уравнения. ОДУ n-го порядка имеет вид F(x,y,y’,..yn)=0. Y(x)-неизвестная функция аргумента х. F-заданная в некоторой области функция. |
14. Теорема существования и единственности решения задачи Коши для диф. ур-ния первого порядка. Поле направлений, изоклины.
Уравнения 1-го порядка имеет вид F(x,y,y’)=0 (1)
Это уравнение называют неразрешенным относительно производной y’. Уравнение разрешенное относительно производной имеет вид (2) y’=f(x,y). Решением уравнения 2 называют непрерывно диф-ю функцию y=ϕ(x), обращающую y’=f(x,y) в тождество в области Д-области задания функции f.
y’=x2; y=(x3/3)+C. Одной из основных задач теории диф. уравнений является задача Коши, которая формулируется так:
Найти решение уравнения y’=f(x,y) удовлетворяющее условию y(x0)=y0 (3). Х0, у0-начальные данные.
Теорема Коши: если функция f –непрерывна в некоторой области Д и имеет в ней непрерывную частную производную δϕ/δy, то существует решение задачи и это решение единственное. Доказательство этой теоремы основано на решении так называемого интегрального уравнения методом последовательных приближений.
Последовательное приближение строится по формуле: y’=f(x,y); y(x0)=y0

 На плоскости ОХУ решение y=ϕ(x) определяет некоторую кривую, которую называют интегральной. Задача Кошизаключается в том, что необходимо найти ту интегральную кривую, которая проходит через точку с координатами х0,у0. Область Д называют областью единственности решения задачи.
Общим решением уравнения y’=f(x,y) в области единственности Д называют функцию y=ϕ(x,с), зависящую от производной постоянной С и обладающую следующими св-вами:
1) При любом значении С эта функция обращает y’=f(x,y) в тождество.
На плоскости ОХУ решение y=ϕ(x) определяет некоторую кривую, которую называют интегральной. Задача Кошизаключается в том, что необходимо найти ту интегральную кривую, которая проходит через точку с координатами х0,у0. Область Д называют областью единственности решения задачи.
Общим решением уравнения y’=f(x,y) в области единственности Д называют функцию y=ϕ(x,с), зависящую от производной постоянной С и обладающую следующими св-вами:
1) При любом значении С эта функция обращает y’=f(x,y) в тождество.
|
| 2) Каковы бы ни были начальные данные х0,у0 найдется такое значение произвольной постоянной с0, что функция y=ϕ(x,с0) будет удовлетворять начальному условию y(x0)=y0. Решение полученное из общего при конкретном значении С (может быть ±∞) называется частным. Если неизвестная функция найдена неявно, то выражение вида Ф(х,у,с)=0 называют общим интегралом уравнения y’=f(x,y), а Ф(х,у)=0 наз-ют частным интегралом. Общему решению уравнения соответствует семейство интегральных кривых. Процесс нахождения решения дифф. уравнения называется интегрированием. Если в каждой точке интегральной кривой нарушается единственность, то через каждую точку проходит еще 1 кривая имеющая в этой точке ту же самую касательную, то такую кривую называют особой интегральной кривой. А решение ей соответствующее называют особым решением. Особая интегральная кривая является огибающей семейства интегральных кривых. Особое решение не содержится в общем ни при каком значении произвольной постоянной С. Поле направлений, изоклины. Дифференциальное уравнение первого порядка y’ = f(x,y) определяет в каждой точке (x,y), где существует функция f(x,y), значение y’, т.е. угловой коэффициент касательной к интегральной кривой в этой точке. Если в каждой точке области D задано значение некоторой величины, то говорят, что в области D задано поле этой величины. Таким образом, дифференциальное уравнение (1) определяет поле направлений. Тройка чисел (x,y,y’) определяет направление прямой, проходящей через точку(x,y). Совокупность отрезков этих прямых дает геометрическую картину поля направлений. Задача интегрирования дифференциального уравнения (1) может быть теперь истолкована так: найти такую кривую, чтобы касательная к ней в каждой точке имела направление, совпадающее с направлением поля в этой точке. |
Задача построения интегральной кривой часто решается введением изоклин. Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым имеют одно и тоже направление. Семейство изоклин дифференциального уравнения (1) определяется уравнением
F(x,y)=k, где k —параметр. Придавая параметру k близкие числовые значения, получаем достаточно густую сеть изоклин, с помощью которых можно приближенно построить интегральные кривые дифференциального yравнения (1).
Замечание 1. Нулевая изоклина f(x,y)=0 дает уравнение линий, на которых могут находиться точки максимума и минимума интегральных кривых.
Для большей точности построения интегральных кривых находят также геометрическое место точек перегиба. Для этого находят y’’ в силу уравнения:
 и приравнивают ее нулю. Линия, определяемая уравнением
и приравнивают ее нулю. Линия, определяемая уравнением
 и есть возможное геометрическое место точек перегиба.
Замечание 2. Точки пересечения двух или нескольких изоклин могут быть особыми точками дифференциального уравнения (1), т.е. такими точками, в которых правая часть уравнения (1) не определена.
Рассмотрим уравнение y’=y/x. Семейство изоклин определяется уравнением y/x=k. Это семейство прямых, проходящих через начало координат, так что в начале координат пересекаются изоклины, отвечающие различным наклонам касательных к интегральным кривым. Нетрудно убедиться, что общее решение данного уравнения имеет вид y=Cx и точка (0,0) является особой точкой дифференциального уравнения. Здесь изоклины являются интегральными кривыми уравнения.
и есть возможное геометрическое место точек перегиба.
Замечание 2. Точки пересечения двух или нескольких изоклин могут быть особыми точками дифференциального уравнения (1), т.е. такими точками, в которых правая часть уравнения (1) не определена.
Рассмотрим уравнение y’=y/x. Семейство изоклин определяется уравнением y/x=k. Это семейство прямых, проходящих через начало координат, так что в начале координат пересекаются изоклины, отвечающие различным наклонам касательных к интегральным кривым. Нетрудно убедиться, что общее решение данного уравнения имеет вид y=Cx и точка (0,0) является особой точкой дифференциального уравнения. Здесь изоклины являются интегральными кривыми уравнения.
|
15. Диф. ур-ния первого порядка, интегрируемые в квадратурах: ур-ния с разделяющимися переменными, однородные.
Диф. уравнения 1-го порядказаписанные в форме дифференциала имеют вид: Р(х,у)dx+Q(x,y)dy=0. Уравнением с разделяющимися переменными называется уравнение вида М1(х)*N1(y)dx+M2(x)*N2(y)dy=0 (1). Разделив 1-е на N1(y)*M2(x), получим: М1(х)/М2(х)dx+N2(y)/N1(y)dy=0 (2). Уравнение 2 называют уравнением с разделенными переменными.
При делении переменных могли быть утеряны решения, которые являются корнями уравнений М2(х)=0 N1(y)=0. Эти решения могут быть как частными так и особыми.
К уравнениям с разделяющимися переменными приводятся ур-я вида: y’=f(ax+by+c), a,b,c – константы. Вводим новую ф-ю z=ax+by+c или (z=ax+by). Выбор подстановки влияет на процесс нахождения интеграла. Учитывая, что z’=a+by’; y’=(z’-a)/b. После подстановки получаем (z’-a)/b=f(z) или dz/dx=b*f(z)+a после деления переменных получаем dz/(b*f(z)+a)=dx
Однородные уравнения и приводящиеся к ним.
f(x,y)=x4-x2*y2+5xy3+x3y=(λx)4-(λ2x2)(λ2y2)+5(λx)(λy)3+(λx)3*λy=λ4f(x,y)
Надо проверить на однородность. Функция являетсяоднородной, если для нее выполняется равенство f(λx,λy)=λmf(x,y). Число mназ-ют порядком однородности. Если в ур-и Р(х,у)dx+Q(x,y)dy=0 (1) P(x,y);Q(x,y) - являются однородными ф-ми одной и той же степени однородности, то 1 называют однородным ур-ем.
Однородноеур-е приводится к ур-ю с разделяющейся переменной с помощью подстановки z=y/x (2). Из 2 имеем y=z*x, тогда dy=xdz+zdx. Подставляя в 1 получим P(x,zx)dx+Q(x,zx)*(xdz+zdx)=0. Т.к. P,Qоднородное, например, степени m, то, считая λ=х, будем иметь xmP(1,z)dx+xmQ(1,z)xdz+ xmQ(1,z)zdx=0 или(P(1,z)+Q(1,z)*z)dx+Q(1,z)xdz=0
После деления переменных будем иметь dx/x+Q(1,z)/(P(1,z)+Q(1,z)*z)*dz=0
Общий интеграл запишется 
|
Утерянными решениями могут быть x=0 или P(1,z)+Q(1,z)z=0 эти решения могут быть как частными, так и особыми.
Ур-я приводящиеся к однородным.
уравнения вида y’=f((a1x+b1y+c1)/(a2x+b2y+c2))
1)
 Вводится подстановка
X=
Вводится подстановка
X=  +α
Y=ӯ+β
α,βявляются решением системы.
a1α+b1 β+c1=0
a2α+b2 β+c2=0
относительно нового аргумента +α
Y=ӯ+β
α,βявляются решением системы.
a1α+b1 β+c1=0
a2α+b2 β+c2=0
относительно нового аргумента  и новой функции ӯ уравнение становится однородным.
Решается подстановкой z= ӯ/ и новой функции ӯ уравнение становится однородным.
Решается подстановкой z= ӯ/  .
2) Δ=0
a1 =ka2
b1=kb2
уравнение имеет вид
у’=f((k*(a2x+b2y)+c1)/(a2x+b2y+c2)) приводит к уравнению с разделяющимися переменными
подстановка -z=a2x+b2y
2)обобщенные однородные уравнения
Уравнение P(x,y)dx+Q(x,y)dy=0 называют обобщенным однородным если существует такое число k что левая часть уравнения становится однородной ф-цией если считать x,y,dx,dy- величинами соответственно порядков 1,k,0,k-1 обобщенное однородное уравнение сводится к подстановке z=y/xk. .
2) Δ=0
a1 =ka2
b1=kb2
уравнение имеет вид
у’=f((k*(a2x+b2y)+c1)/(a2x+b2y+c2)) приводит к уравнению с разделяющимися переменными
подстановка -z=a2x+b2y
2)обобщенные однородные уравнения
Уравнение P(x,y)dx+Q(x,y)dy=0 называют обобщенным однородным если существует такое число k что левая часть уравнения становится однородной ф-цией если считать x,y,dx,dy- величинами соответственно порядков 1,k,0,k-1 обобщенное однородное уравнение сводится к подстановке z=y/xk.
|
16. Диф. ур-ния первого порядка, интегрируемые в квадратурах: линейное уравнение, уравнение Бернулли.
Линейное уравнение.
Линейным уравнением называют уравнение вида y’+p(x)*y=q(x) (1)
Уравнение 1 является линейным неоднородным, если  . y’+p(x)y=0 (2).
Уравнение 2 называют соответствующим однородным для 1. если в 1 коэффициент p(x) и свободный член q(x) непрерывно на некотором интервале I то существует на этом интервале единственное решение уравнения 1 удовлетворяющее начальному условию (3) (x0,y0)? I
Уравнение Бернулли.
Уравнением Бернулли называют уравнение вида y’+p(x)*y=q(x)*yn (1)
Приведем 1 к линейному уравнению после деления на уn
y’*y-n+p(x)y1-n=q(x)
z=y1-n (2)
Дифф-ем 2 получаем z’=(1-n)*y-n*y’
Z’/(1-n)+p(x)z=q(x) (3)
Ур-е 3 является линейным относительно z. Ур-ние может быть ур-нием Бернулли и относительно х, как ф-ция у,тогда она примет вид dx/dy+p(y)x=q(y)xn (4)
Ур-ние 1 или 4 имеют особое решение у=0 или х=0 только при 0<n<1 . y’+p(x)y=0 (2).
Уравнение 2 называют соответствующим однородным для 1. если в 1 коэффициент p(x) и свободный член q(x) непрерывно на некотором интервале I то существует на этом интервале единственное решение уравнения 1 удовлетворяющее начальному условию (3) (x0,y0)? I
Уравнение Бернулли.
Уравнением Бернулли называют уравнение вида y’+p(x)*y=q(x)*yn (1)
Приведем 1 к линейному уравнению после деления на уn
y’*y-n+p(x)y1-n=q(x)
z=y1-n (2)
Дифф-ем 2 получаем z’=(1-n)*y-n*y’
Z’/(1-n)+p(x)z=q(x) (3)
Ур-е 3 является линейным относительно z. Ур-ние может быть ур-нием Бернулли и относительно х, как ф-ция у,тогда она примет вид dx/dy+p(y)x=q(y)xn (4)
Ур-ние 1 или 4 имеют особое решение у=0 или х=0 только при 0<n<1
|
17. Диф. ур-ния первого порядка, интегрируемые в квадратурах: уравнения в полных дифференциалах, интегрирующий множитель.
Уравнения в полных дифференциалах
Если левая часть ур-я P(x,y)dx+Q(x,y)dy=0 представляет собой полный дифференциал некой ф-ииU(x,y),то (1) наз-ют ур-ем в полныхдиф-лах.
Такое ур-ние можно записать в виде d(u(x,y))=0, то общее решение будет иметь вид U(x,y)=C (1’). С=сonst. Согласно определению полного дифференциала имеем du=(δu/δx)*dx+(δu/δy)*dy (2). Сравнивая (1,1’,2), получим δu/δx=P(x,y);δu/δy=Q(x,y) (3). Дифференцируя 1-е из(3)по у(2-ое по х), имеем δ2u/(δxδy)=δP/δy=δQ/δx (4)- необходимое и достаточное условие для того, чтоб (1) было ур-ем в полныхдиф-лах.
Алгоритм решения:
1) Если выполнено условие 4 то решение уравнения 1 ищем в виде U(x,y)=C
2)Для нахождения u согласно 1 составляем систему δu/δx=P(x,y);δu/δy=Q(x,y).
3)Интегрируем одно из ур-й 3. Если первое, то по х считая у постоянным (если 2 по у).получаем  ; 2: ; 2:  4)Диф-ем найденную ф-ю u по у (если 2 то по х).сравниваем найденную производную с правой частью второго уравнения. Получаем (δ/δy)*
4)Диф-ем найденную ф-ю u по у (если 2 то по х).сравниваем найденную производную с правой частью второго уравнения. Получаем (δ/δy)* 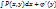 =Q(x,y)-для 1(для 2 аналогично)
5)Определив из полученных равенств =Q(x,y)-для 1(для 2 аналогично)
5)Определив из полученных равенств  (или (или  ). Интегрируем найденные ф-и и подставляем их в выражение для ф-и u.
6)Приравниваем полученную ф-ю u к произвольной константе. Получаем общий интеграл уравнения 1. Особых решений не имеет. ). Интегрируем найденные ф-и и подставляем их в выражение для ф-и u.
6)Приравниваем полученную ф-ю u к произвольной константе. Получаем общий интеграл уравнения 1. Особых решений не имеет.
|
| Интегрирующий множитель. Пусть P(x,y)dx+Q(x,y)dy=0 не является уравнением в полных диференциалах, но существует такая ф-ция μ(х,у), после умножения на которую левая часть 1 становится полным дифференциалом μP(x,y)dx+μQ(x,y)dy=0 (2). Для 2 имеем δ(μP)/δy= δ(μQ)/δx (3). Из 3 μ(δP/δy)+P(δμ/δy)=μ(δQ/δx)+Q(δμ/δx) (4). 4 явл-ся уравнением в частных производных относительно неизвестной ф-ии μ(х,у) и в общем случае переменна. |
18. Общие понятия о диф. ур-ниях высших порядков. Задача Коши. Теорема существования и единственности решения задачи Коши.
ОДУ n-го порядка имеет вид F(x,y,y’,..yn)=0 (1), F-заданная в некоторой области D функция. Уравнение вида  (2) называют разрешенным относительно старшей производной.
Задача Коши для (2) формулируется так: найти решения (2) удовлетворяющие начальным условиям (3)y(x0)=y0; y’(x0)=y’0; (2) называют разрешенным относительно старшей производной.
Задача Коши для (2) формулируется так: найти решения (2) удовлетворяющие начальным условиям (3)y(x0)=y0; y’(x0)=y’0;  ;(3). Теорема сущ-я и единственности решения задачи Коши: если функция f и ее частные производные δf/δy, δ f/δy’, δf/δy(n)- непрерывна в некоторой области D и точка(х0,y0,y’0…y(n-1)0)?D, то существует интеграл (x0-δ,x0+δ)?D, на котором ур-ние(2) имеет решение удовлетворяющее условию (3) и это решение единственное. Область D называют областью единственности решения задачи 2-3. Решением ур-ния 2 называют n раз непрерывно диф-ю ф-циюy=ϕ(x), обращающую 2 в верное тождество. Общим реш-ем ур-я 2 наз-ют ф-ю y= ϕ(x,C1,C2…Cn) в области ед-стиD. С1,С2,Сn- производные постоянные которые обладают следующими св-вами:
1) при любых значениях Сii=1,n--.эта ф-я удовлетворяетур-нию 2
2) каковы бы ни были начальные условия 3, всегда найдется набор постоянныхC10,C20…Cn0, что ф-цияy=ϕ(x,C10,C20…Cn0) будет удовлетворять условиям 3. Решение, полученное из общего при конкретных значениях Сiх, называют частными.Если искомая ф-ция найдена неявным образом, то выражение вида Ф(х,у,С1,С2…Сn) называют общим интегралом. Частный интеграл получается из общего при конкретных значениях Сi. Если удается понизить порядок ур-ния 1 на единицу,то выражение вида F(x,y,y’…y(n-1),C1)=0.Если на nединиц, то F~(x,y,y’…y(n-1),C2,…Ck)=0 называют к-ым интегралом. ;(3). Теорема сущ-я и единственности решения задачи Коши: если функция f и ее частные производные δf/δy, δ f/δy’, δf/δy(n)- непрерывна в некоторой области D и точка(х0,y0,y’0…y(n-1)0)?D, то существует интеграл (x0-δ,x0+δ)?D, на котором ур-ние(2) имеет решение удовлетворяющее условию (3) и это решение единственное. Область D называют областью единственности решения задачи 2-3. Решением ур-ния 2 называют n раз непрерывно диф-ю ф-циюy=ϕ(x), обращающую 2 в верное тождество. Общим реш-ем ур-я 2 наз-ют ф-ю y= ϕ(x,C1,C2…Cn) в области ед-стиD. С1,С2,Сn- производные постоянные которые обладают следующими св-вами:
1) при любых значениях Сii=1,n--.эта ф-я удовлетворяетур-нию 2
2) каковы бы ни были начальные условия 3, всегда найдется набор постоянныхC10,C20…Cn0, что ф-цияy=ϕ(x,C10,C20…Cn0) будет удовлетворять условиям 3. Решение, полученное из общего при конкретных значениях Сiх, называют частными.Если искомая ф-ция найдена неявным образом, то выражение вида Ф(х,у,С1,С2…Сn) называют общим интегралом. Частный интеграл получается из общего при конкретных значениях Сi. Если удается понизить порядок ур-ния 1 на единицу,то выражение вида F(x,y,y’…y(n-1),C1)=0.Если на nединиц, то F~(x,y,y’…y(n-1),C2,…Ck)=0 называют к-ым интегралом.
|
| 19. Уравнения, допускающие понижения порядка. Интегрирование дифференциальных уравнений n-го порядка удается выполнить только в некоторых частных случаях. Укажем несколько классов уравнений, которые допускают понижение порядка. Уравнение вида y(n)= f(x). Решение этого уравнения находится n-кратным интегрированием, а именно: y(n)= f(x), y(n-1)=∫f(x)dx+c1=f1(x)+c1 y(n-2)= ∫[f1(x) +c1]dx=f2(x)+c1x+c2 y=fn(x)+ c1/(n-1)!*x(n-1)+ c2/(n-2)!*x(n-2)+..+cn-1x+cn гдеfn(x)=∫∫…∫f(x)dxn. В силу того, что, c1/(n-1)!, c2/(n-2)!,… являются постоянными величинами, то общее решение может быть записано и так: y=fn(x)+ c1x(n-1)+ c2x(n-2)+..+cn-1x+cn 2. Уравнение вида F(x, y’,..., y(n)) = 0 – это уравнение, которое явно не содержит искомой функции y и ее производных до порядка k -1 включительно. С помощью замены y’= z(x) понижается порядок уравнения: F(x, z, z’,..., z(n-1)) = 0. Допустим, что для полученного уравнения можно найти общее решение z(x) =ϕ(x,C1,...,Cn-1). Тогда решение искомой функции y=∫ϕ(x,C1,...,Cn-1)dx+cn. 3. Уравнение вида F(y, y’,..., y(n)) = 0, которое не содержит явно не зависимой перемененной. Подстановкой y’=z(y); y’’=dz/dy*dy/dx=z’*z; y’’’=d(y’’) /dy*dy/dx=(z’’*z+z’*z’)y’=z’’z2+z’2z допустим что это уравнение имеет общее решение z=ϕ(y,c1,c2,…,cn-1) dy/dx= ϕ(y,c1,c2,…,cn-1) dy/ ϕ(y,c1,c2,…,cn-1)=dx тогдаобщийинтегралx=∫ dy/ ϕ(y,c1,c2,…,cn-1)+cn |
| 4. Уравнение F (x, y, y’,..., y(n)) = 0, однородное относительно функции y и ее производных. Это значит, что F (x, λy,λ y’,...,λy(n)) =λm F (x, y, y’,..., y(n)) порядок уравнения понижается подстановкой z= y’/y. 5) Уравнение вида d/ dx (F (x, y, y’,..., y(n -1))) = 0 − это такое уравнение, у которого левая часть может быть представлена как полная производная по x от некоторой функции F(x, y,y.,..., y(n-1)). Если проинтегрируем его по x, то получим новое уравнение, порядок которого на единицу ниже порядка исходного уравнения. 6) Уравнение F (x, y, y’,..., y(n)) = 0 называется обобщенным однородным, если существует такое число k, при котором левая часть этого уравнения становится однородной функцией некоторой степени m относительно всех аргументов при условии, что x, y, y’,..., y(n) считаются величинами соответственно 1,k,(k -1),...,(k - n) -ой степени. Чтобы узнать, будет ли уравнение обобщенным однородным и найти число k, необходимо сравнить показатели степеней, в которые число k будет входить согласно с определением каждого члена уравнения. Если полученные уравнения для k будут несовместными, то дифференциальное уравнение не является обобщенным. После того, как число k найдено, необходимо сделать замену переменных x = et, y = zekt, где z = z(t) – новая неизвестная функция, а t – новая независимая переменная. Получаем уравнение, в которое не входит независимая переменная x. Порядок такого уравнения понижается одним из ранее рассмотренных способов |
20. Понятие о краевых задачах. Линейная краевая задача.
Наряду с задачей Коши для ур-ния 2 ставятся так называемые краевые (граничные задачи), в которых решениеур-ния требуется найти при определённых условиях, заданных на концах указанного отрезка.
В то время, как краевые условия задаются исключительно на граничных точках области, где ищется решение, начальные условия могут оказаться заданными на определённом множестве точек внутри области. Например, уравнение
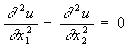 имеет бесконечное множество решений u (x1, х2) = f (x1+x2) + f1(x1-x2), где f и f1 — произвольные дважды непрерывно дифференцируемые функции.
Однако в прямоугольнике —а ≤ x2 ≤ a, 0 ≤ x1 ≤ l, плоскости с прямоугольными декартовыми координатами x1, x2 уравнение (1) имеет единственное решение u (x1, x2), удовлетворяющее краевым
u (0, x2) = 0, u (l, x2) = 0, —а ≤ x2 ≤ a, (2)
и начальным
u (x1, 0) = φ(x1),
имеет бесконечное множество решений u (x1, х2) = f (x1+x2) + f1(x1-x2), где f и f1 — произвольные дважды непрерывно дифференцируемые функции.
Однако в прямоугольнике —а ≤ x2 ≤ a, 0 ≤ x1 ≤ l, плоскости с прямоугольными декартовыми координатами x1, x2 уравнение (1) имеет единственное решение u (x1, x2), удовлетворяющее краевым
u (0, x2) = 0, u (l, x2) = 0, —а ≤ x2 ≤ a, (2)
и начальным
u (x1, 0) = φ(x1),
 условиям. При этом дважды непрерывно дифференцируемые функции φ и ψ считаются наперёд заданными. Если переменное x2 есть время t, то решение u (х, t) уравнения (1), удовлетворяющее условиям (2) и (3), описывает колебание упругой струны длины l с концами, закрепленными в точках (0, 0) и (0, l).
Вообще краевыми называют задачи, в которых в заданной области G пространства независимых переменных (x1,..., xn) = х ищется решение u (х) = u (x1,..., xn) уравнения Du (x) = 0, x ∈ G (4).
условиям. При этом дважды непрерывно дифференцируемые функции φ и ψ считаются наперёд заданными. Если переменное x2 есть время t, то решение u (х, t) уравнения (1), удовлетворяющее условиям (2) и (3), описывает колебание упругой струны длины l с концами, закрепленными в точках (0, 0) и (0, l).
Вообще краевыми называют задачи, в которых в заданной области G пространства независимых переменных (x1,..., xn) = х ищется решение u (х) = u (x1,..., xn) уравнения Du (x) = 0, x ∈ G (4).
|
| При требовании, что искомая функция u (х) на границе S области G удовлетворяет краевому (граничному) условиюBu (у) = 0, y ∈ S, (5), где D и В — заданные операторы. Граница S называется носителем краевых данных (5). Когда операторы D и В линейны, К. з. (4), (5) называется линейной. |
21. Линейные однородные диф. ур-ния высших порядков и свойства их решений.
Линейным дифференциальным уравнением n-го порядка называют уравнение вида  где функции ai(x), непрерывны на некотором интервале i = (a;b)
существует решение ур-ния (1), удовлетворяющее начальным условиям y(x0)*y0; y’(x0)*y’0;yn-1(x0)*y0n-1 где х0? I, и это решение единственное.
Из этого утверждения следует, если решение 1 удовлетворяет нулевым начальным условиям y(x0)=0; y’(x0)=0; yn-1(x0)=0, то оно тождественно обращается в ноль на всем интервале I. Если ввести линейный оператор L(y)= yn+a1(x)*yn-1+…+an(x)*y,то L(y)=0
Свойство решений ур-ния (1):
1)Если у1 и у2 есть решение (1),то их сумма у1+у2 также есть решение (1)- это св-во следует из линейности оператора L(у1 + у2)=L(у1)+L(у2)=0+0=0
2)Если у – решение (1),то С*у, С=const,также реш-е (1). L(Cy)=CL(y)=C*0=0
3)Если комплексно значнаяu(x)+i*v(x); (i2=-1 – линейная еденица) являетсярешением ур-ния (1), то ее действительная часть u(x) и мнимая часть v(x) также являются решением ур-ния (1).
L(u(x)+i*v(x))=L(u(x))+i*L(v(x))=0; L(u(x))=0 и L(v(x))=0
Из св-в 1 и 2 следует,что множество решений ур-ния (1) обретает линейное пространство, поэтому для того, чтобы найти все решения (1) необходимо построить так называемую фундаментальную систему решений, т.е. ситему линейно независимых решений.
Напомним,что система ф-ций у1(х), у2(х)… уn(х) является линейно независимой, если равенство α1*у1+ α2*у2+ αn*уn=0 (3) выполняется тогда и только тогда,когда все αi=0. Если же существует хотя бы одна из постоянных αi-ых отличная от нуля при которой (3)имеет место, то системы функций у1…уnназывают линейно зависимой.
где функции ai(x), непрерывны на некотором интервале i = (a;b)
существует решение ур-ния (1), удовлетворяющее начальным условиям y(x0)*y0; y’(x0)*y’0;yn-1(x0)*y0n-1 где х0? I, и это решение единственное.
Из этого утверждения следует, если решение 1 удовлетворяет нулевым начальным условиям y(x0)=0; y’(x0)=0; yn-1(x0)=0, то оно тождественно обращается в ноль на всем интервале I. Если ввести линейный оператор L(y)= yn+a1(x)*yn-1+…+an(x)*y,то L(y)=0
Свойство решений ур-ния (1):
1)Если у1 и у2 есть решение (1),то их сумма у1+у2 также есть решение (1)- это св-во следует из линейности оператора L(у1 + у2)=L(у1)+L(у2)=0+0=0
2)Если у – решение (1),то С*у, С=const,также реш-е (1). L(Cy)=CL(y)=C*0=0
3)Если комплексно значнаяu(x)+i*v(x); (i2=-1 – линейная еденица) являетсярешением ур-ния (1), то ее действительная часть u(x) и мнимая часть v(x) также являются решением ур-ния (1).
L(u(x)+i*v(x))=L(u(x))+i*L(v(x))=0; L(u(x))=0 и L(v(x))=0
Из св-в 1 и 2 следует,что множество решений ур-ния (1) обретает линейное пространство, поэтому для того, чтобы найти все решения (1) необходимо построить так называемую фундаментальную систему решений, т.е. ситему линейно независимых решений.
Напомним,что система ф-ций у1(х), у2(х)… уn(х) является линейно независимой, если равенство α1*у1+ α2*у2+ αn*уn=0 (3) выполняется тогда и только тогда,когда все αi=0. Если же существует хотя бы одна из постоянных αi-ых отличная от нуля при которой (3)имеет место, то системы функций у1…уnназывают линейно зависимой.
|
Для установления линейной зависимости функций пользуются определителем Вронского:
 Имеет место утверждение: пусть у1(х)…yn(x) есть решениеур-ния (1),тогда а)если в некоторой точке х0W(х0)≠0 функции у1(х)…yn(x) – линейно независимы
б)Если существуетхотя бы одна точка х0 такая,что W(х0)=0, то ф-ция линейно зависима.Из этого условия следует, что определитель Вронского,составленный из фундаментальной системы решений, не образуется ни водой точке интервала I.
Имеет место утверждение: пусть у1(х)…yn(x) есть решениеур-ния (1),тогда а)если в некоторой точке х0W(х0)≠0 функции у1(х)…yn(x) – линейно независимы
б)Если существуетхотя бы одна точка х0 такая,что W(х0)=0, то ф-ция линейно зависима.Из этого условия следует, что определитель Вронского,составленный из фундаментальной системы решений, не образуется ни водой точке интервала I.
|
| 22. Структура общего решения неоднородных линейных диф. ур-ний высших порядков. Рассмотрим линейное неоднородное дифференциальное уравнение y (n) + an -1(x) y (n - 1) +... + a 1(x) y ' + a 0(x) y = f (x). Общим решением этого уравнения на отрезке [ a; b ] называется функция y = Φ(x, C 1,..., Cn), зависящая от n произвольных постоянных C 1,..., Cn и удовлетворяющая следующим условиям: − при любых допустимых значениях постоянных C 1,..., Cn функция y = Φ(x, C 1,..., Cn) является решением уравнения на [ a; b ]; − какова бы ни была начальная точка (x 0, y 0, y 1,0,..., yn − 1,0), x 0∈ [ a; b ], существуют такие значения C 1 = C 10,..., Cn = Cn 0, что функция y = Φ(x, C 10,..., Cn 0) удовлетворяет начальным условиям y (x 0) = y 0, y '(x 0) = y 1,0,..., y (n − 1) (x 0) = yn − 1,0. Справедливо следующее утверждение (теорема о структуре общего решения линейного неоднородного уравнения). Если все коэффициенты уравнения линейного однородного дифференциального уравнения непрерывны на отрезке [ a; b ], а функции y 1(x), y 2(x),..., yn (x) образуют фундаментальную систему решенийсоответствующего однородного уравнения, то общее решение неоднородного уравнения имеет вид y (x, C 1,..., Cn) = C 1 y 1(x) + C 2 y 2(x) +... + Cnyn (x) + y *(x), где C 1,..., Cn — произвольные постоянные, y *(x) — частное решение неоднородного уравнения. |
23. Линейная зависимость и независимость системы функций. Определитель Вронского. Линейные однородные диф. ур-ния с постоянными коэффициентами. Характеристическое уравнение. Метод Эйлера.
Система функций y 1(x), y 2(x), …, yn (x) называется линейно зависимой на интервале (a, b), если существует набор постоянных коэффициентов  , не равных нулю одновременно, таких, что линейнаякомбинация этих функций тождественно равна нулю на (a, b): , не равных нулю одновременно, таких, что линейнаякомбинация этих функций тождественно равна нулю на (a, b):  для для  . Если равенство . Если равенство  для для  возможно только при возможно только при  , система функций y 1(x), y 2(x), …, yn (x) называется линейно независимой на интервале (a, b). Определитель Вронского (вронскиан) системы n - 1 раз дифференцируемых функций y 1(x), y 2(x), …, yn (x) - определитель , система функций y 1(x), y 2(x), …, yn (x) называется линейно независимой на интервале (a, b). Определитель Вронского (вронскиан) системы n - 1 раз дифференцируемых функций y 1(x), y 2(x), …, yn (x) - определитель  Теорема о вронскиане линейно зависимой системы функций. Если система функций y 1(x), y 2(x), …, yn (x) линейно зависима на интервале (a, b), то вронскиан этой системы тождественно равен нулю на этом интервале.
Теорема о вронскиане линейно зависимой системы функций. Если система функций y 1(x), y 2(x), …, yn (x) линейно зависима на интервале (a, b), то вронскиан этой системы тождественно равен нулю на этом интервале.
|
Линейные однородные уравнения с постоянными коэффициентами
Рассмотрим уравнение  0 (1), где 0 (1), где  - действительные числа. Будем решать ур (1) методом Эйлера. Согласно методу, решение ищем в виде - действительные числа. Будем решать ур (1) методом Эйлера. Согласно методу, решение ищем в виде  (2), где (2), где  - некоторый параметр. Продифференцируем (2) n раз и подставим в (1) - некоторый параметр. Продифференцируем (2) n раз и подставим в (1)
 , ,  ,…, ,…,  . .  После деления на
После деления на  получим получим  (3)
Таким образом, для того чтобы (2) было решением (1) необходимо, чтобы (3)
Таким образом, для того чтобы (2) было решением (1) необходимо, чтобы  удовлетворяло уравнению (3). Ур (3) называют характеристическим для (1). Рассмотрим следующие случаи
1.Пусть корни характеристического уравнения (3) различные действительные удовлетворяло уравнению (3). Ур (3) называют характеристическим для (1). Рассмотрим следующие случаи
1.Пусть корни характеристического уравнения (3) различные действительные  Тогда согласно (2) каждому из этих корней будет соответствовать решение
Тогда согласно (2) каждому из этих корней будет соответствовать решение
 . Легко показать, что определитель Вронского состоит из этих решений, например в точке х=0 отличен от 0, т.е. система решений . Легко показать, что определитель Вронского состоит из этих решений, например в точке х=0 отличен от 0, т.е. система решений  линейно не зависимая, а значит, согласно теореме о структуре, общее решение в этом случае имеет вид: линейно не зависимая, а значит, согласно теореме о структуре, общее решение в этом случае имеет вид:
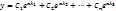 , где С- произвольные постоянные.
2. Пусть среди корней ур. (3) есть комплексный , где С- произвольные постоянные.
2. Пусть среди корней ур. (3) есть комплексный  . Т.к. коэффициенты уравнения (3) действительные, то обязательно есть комплексно сопряженный корень . Т.к. коэффициенты уравнения (3) действительные, то обязательно есть комплексно сопряженный корень
 . Пусть имеем пару . Пусть имеем пару  Согласно формуле (2) имеем Согласно формуле (2) имеем  По формуле Эйлера представления комплексной экспоненты в тригонометрической форме будем иметь:
По формуле Эйлера представления комплексной экспоненты в тригонометрической форме будем иметь:  . .
|
Таким образом, паре комплексных сопряженных корней  соответствует два решения
соответствует два решения
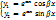 . Легко показать, что функции . Легко показать, что функции  - линейно не
зависимые.
А значит, общее решение в этом случае будет иметь вид: - линейно не
зависимые.
А значит, общее решение в этом случае будет иметь вид:
 3. Пусть среди корней ур (3) есть действительный kкратный корень λ. Известно, что если λ-k кратный корень, то L(λ)=
3. Пусть среди корней ур (3) есть действительный kкратный корень λ. Известно, что если λ-k кратный корень, то L(λ)=  = =  ; Пользуясь этим утверждением и используя формулу Ньютона-Лейбница дифференцируем произведения двух функций. Легко доказать, что k кратному действительному корню будет соответствовать kрешений: ; Пользуясь этим утверждением и используя формулу Ньютона-Лейбница дифференцируем произведения двух функций. Легко доказать, что k кратному действительному корню будет соответствовать kрешений:  . Общее решение
в этом случае имеет вид: . Общее решение
в этом случае имеет вид:  .
Если имеем kкратную комплексно-сопряженную пару .
Если имеем kкратную комплексно-сопряженную пару  (всего 2k корней). Общее решение имеет вид: (всего 2k корней). Общее решение имеет вид:

|
28. Основные понятия теории устойчивости по Ляпунову.
Пусть имеем систему дифференциальных уравнений
 (1)
Решение (1)
Решение  системы (1), удовлетворяющее начальным условиям системы (1), удовлетворяющее начальным условиям   , называется устойчивым no Ляпунову при , называется устойчивым no Ляпунову при 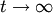 , если для любого , если для любого 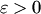 существует существует 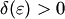 такое, что для всякого решения такое, что для всякого решения   , системы (1), начальные значения которого удовлетворяют условиям , системы (1), начальные значения которого удовлетворяют условиям  (2)
имеют место неравенства (2)
имеют место неравенства  (3)
для всех (3)
для всех 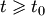 .
Если при сколь угодно малом .
Если при сколь угодно малом  хотя бы для одного решения хотя бы для одного решения   , неравенства (3) не выполняются, то решение , неравенства (3) не выполняются, то решение  называется неустойчивым.
Если, кроме выполнения неравенств (3) при условии (2) выполняется также условие называется неустойчивым.
Если, кроме выполнения неравенств (3) при условии (2) выполняется также условие  (4)
то решение (4)
то решение  , называется асимптотически устойчивым.
Исследование на устойчивость решения , называется асимптотически устойчивым.
Исследование на устойчивость решения   , системы (1) можно свести к исследованию на устойчивость нулевого (тривиального) решения , системы (1) можно свести к исследованию на устойчивость нулевого (тривиального) решения   , некоторой системы, аналогичной системе (1), , некоторой системы, аналогичной системе (1),
|
27. Линейные неоднородные системы диф. ур-ний с постояннымикоэф.
Рассмотрим систему (1)
 А – действительная матрица, f(x) – вектор-функция.
Если в (1) f(x) имеет специальный вид А – действительная матрица, f(x) – вектор-функция.
Если в (1) f(x) имеет специальный вид
 то, частное решение, в случае отсутствия резонанса, находится по темже правилам, что и для неоднородного уравнения.
Если пара α±iβвстречается k-раз то, в частном решении вместо множителя xkвозникают многочлены на k единиц больше чем самая большая степень многочленов правой части.
1) α±iβ – не корень то, частное решение, в случае отсутствия резонанса, находится по темже правилам, что и для неоднородного уравнения.
Если пара α±iβвстречается k-раз то, в частном решении вместо множителя xkвозникают многочлены на k единиц больше чем самая большая степень многочленов правой части.
1) α±iβ – не корень  S=max(m,n)
2) α±iβ –k корень кратности S=max(m,n)
2) α±iβ –k корень кратности  Метод вариации заключается в нахождении n–неизвестных функций C1(x),…Cn(x). При нахождении общего решения системы уравнений производится замена постоянных С1,…Сn на соответствующие функции C1(x),…Cn(x). Составляется система из n – уравнений из, которой находим эти неизвестные. После подставляем найденные выше C1(x),…Cn(x) в общее решение и получаем ответ.
Метод вариации заключается в нахождении n–неизвестных функций C1(x),…Cn(x). При нахождении общего решения системы уравнений производится замена постоянных С1,…Сn на соответствующие функции C1(x),…Cn(x). Составляется система из n – уравнений из, которой находим эти неизвестные. После подставляем найденные выше C1(x),…Cn(x) в общее решение и получаем ответ.
|
26. Линейные однородные системы диф. ур-ний с постояннымикоэф. Характеристическое уравнение. Метод Эйлера.
Рассмотрим систему (1)
 –действительная матрица.
Согласно методу Эйлера решение системы (1) будем искать в виде –действительная матрица.
Согласно методу Эйлера решение системы (1) будем искать в виде  (2) λ – некоторый параметр, γ – числовой вектор
Дифференцируя (2) и подставив в (1) получим (2) λ – некоторый параметр, γ – числовой вектор
Дифференцируя (2) и подставив в (1) получим
 (3); Е – единичная матрица.
Система (3) является линейной однородной алгебраической системой относительно неизвестного вектора γ. Для того, чтобы эти системы имели ненулевое решение необходимо чтобы её главный определитель был равен 0.Т.е. (3); Е – единичная матрица.
Система (3) является линейной однородной алгебраической системой относительно неизвестного вектора γ. Для того, чтобы эти системы имели ненулевое решение необходимо чтобы её главный определитель был равен 0.Т.е.  (4)
Характеристическое уравнение для данной системы имеет вид (4)
Характеристическое уравнение для данной системы имеет вид
 (4)
Пусть среди корней (4) есть комплексно-сопряжённые λ1,2α±iβ.Согласно формуле Эйлера будем иметь: (4)
Пусть среди корней (4) есть комплексно-сопряжённые λ1,2α±iβ.Согласно формуле Эйлера будем иметь:
 По свойствам решений системы (1) решениями будут
По свойствам решений системы (1) решениями будут


|
25. Линейные неоднородные диф. ур-ния с постоянными коэф. Метод вариации произвольных постоянных.
Рассмотрим систему (1)
 А – действительная матрица, f(x) – вектор-функция.
Если в (1) f(x) имеет специальный вид А – действительная матрица, f(x) – вектор-функция.
Если в (1) f(x) имеет специальный вид
 то, частное решение, в случае отсутствия резонанса, находится по тем же правилам, что и для неоднородного уравнения.
Если пара α±iβвстречается k-раз то, в частном решении вместо множителя xkвозникают многочлены на k единиц больше чем самая большая степень многочленов правой части.
1) α±iβ – не корень то, частное решение, в случае отсутствия резонанса, находится по тем же правилам, что и для неоднородного уравнения.
Если пара α±iβвстречается k-раз то, в частном решении вместо множителя xkвозникают многочлены на k единиц больше чем самая большая степень многочленов правой части.
1) α±iβ – не корень
Поиск по сайту©2015-2025 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2017-12-12 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |