1. Плотность распределения есть неотрицательная функция:
2. Интеграл в бесконечных пределах от плотности распределения равен единице:
Геометрически эти свойства означают, что:
1) Вся кривая распределения лежит не ниже оси абсцисс
2) Полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
Пример 1
Функция распределения непрерывной случайной величины X задана выражением
Найти:
а) Коэффициент a
б) Плотность распределения f(x)
в) Вероятность попадания величины X на участок от 0,25 до 0,5
Решение:
а) Так как функция распределения величины X непрерывна, то при 
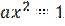откуда 
б) Плотность распределения величины X выражается формулой
в) Вероятность попадания
Пример 2
Случайная величина X подчинена закону распределения с плотностью 
при 
Найти:
а) Коэффициент а
б) Построить график плотности распределения
в) Найти функцию распределения F(x) и построить ее график
г) Определить вероятность попадания на участок от 0 до 
Решение:
а) Для определения коэффициента а воспользуемся свойством плотности распределения
откуда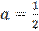 
б) График плотности распределения:
Рисунок 5
в) По формуле 
получаем выражение функции распределения
Рисунок 6
г) Вероятность попадания величины X на заданный отрезок
Методические указание к работе
Автоматические системы регулирования широко применяются при автоматизации технологических процессов на различных объектах. Структурная схема АСР приведена на рисунке 8. Система регулирования состоит из управляющего устройства, регулирующего органа и объекта регулирования.
Рисунок 8 Структурная схема АСР
Выходная величина зависит от входного значения и сигнала поступающего от регулирующего органа. Вероятность появления в замкнутой системе помех приблизительно равна единицы. Поэтому возникает задача определения статистических характеристик одноконтурной автоматической системы регулирования.
Задания для практической работы
Дано:
- аналитическое выражение плотности распределения случайной величины;
- распределение случайной величины.
Требуется:
- определить характер случайной величины;
- определить плотность распределения случайной величины;
- построить график для функции и плотности распределения случайной величины.
Варианты заданий
| Вариант | Задание | Распределение случайной величины |
Задания
Задание №1
Задание №2
Задание №3
Задание №4
Задание №5
Задание №6
Задание №7
Распределение случайной величины
| 
| 
| 
|
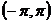
В отчете представить:
- значения плотности распределения случайной величины;
- графики для функции и плотности распределения случайной величины выходного сигнала одноконтурной АСР.
СПИСОК ЛИТЕРАТУРЫ
1. Ястребенецкий М. А., Иванова Г. М. Надежность АСУ ТП. Учебное пособие для вузов. – М.: Энергоатомиздат, 1989. – 264 с.
2. Андык В.С. Теория автоматического управления. Учебное пособие. – Томск: Издательство Томского политехнического института, 2005. – 108с.