МАТЕМАТИКА
Методические указания и контрольные задания
для студентов второго курса заочной формы обучения
всех специальностей, кроме экономических
(IV семестр)
Издание второе, дополненное и переработанное
Брянск 2002
УДК 511
Математика. Методические указания и контрольные задания для студентов второго курса заочной формы обучения всех специальностей, кроме экономических (IV семестр). – 2-е изд., доп. и перераб. – Брянск: БГТУ, 2002. – 24 с.
Разработали: В.К. Леденёва, канд. физ.-мат. наук, доц.;
А.И. Горелёнков, канд. техн. наук, доц.
Рекомендовано кафедрой «Высшая математика»
(протокол №3 от 18.11.01)
Научный редактор Л.А. Гусакова
Редактор издательства Л.Н. Мажугина
Компьютерный набор А.И. Горелёнков
Печатается по изданию: Математика. Методические указания и контрольные задания для студентов второго курса заочной формы обучения (IV семестр), 1998 г.
Т/п. 2002; п. 17
Лицензия №020381 от 24.04.97. Подписано в печать
Формат 60´84 1/16. Бумага офсетная. Печать офсетная.
Печ. л. 1,33. Уч.-изд. л. 1,33. Т. 150 экз. Заказ
Брянский государственный технический университет
241035, г. Брянск, бульвар им. 50-летия Октября, 7
Лаборатория оперативной полиграфии БГТУ, ул. Институтская, 16.
ПРЕДИСЛОВИЕ
Настоящие методические указания охватывают материал разделов курса высшей математики «Теория вероятностей» и «Математическая статистика», по которому студенты второго курса заочной формы обучения выполняют контрольные работы №7, №8.
Каждая тема разбита на пункты, в которых в квадратных скобках [ ] указаны пособия из приведенного списка литература. После изучения определенной темы, необходимо ответить на вопросы для самопроверки и рассмотреть примеры решения задач. Изучив тему, выполнить контрольную работу, оформление которой должно соответствовать требованиям, изложенным в методических указаниях первого семестра.
Список рекомендуемой литературы
1. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1999.*
2. Коваленко И.Н., Филиппова А.А. Теория вероятностей и математичес-кая статистика. – М.: Высш. шк., 1982.*
3. Захаров В.К., Севастьянов Б.А., Чистяков В.П. Теория вероятностей. – М.: Наука, 1983.*
4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высш. шк., 1998.*
5. Иванова В.М. и др. Математическая статистика. – М.: Высш. шк., 1981.*
Тема XIX. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Случайные события
Литература. [1 гл. 2 §1–3, гл. 3, гл. 4, гл. 5 §9, гл. 13 §8]; [2 гл. I §1--3, §5–8, гл. II §2, §4, §6]; [3 §1–4]; [4 гл. 1 §1, гл. 2, гл. 3 §1, §2]; [5 гл. 2, гл. 4 §4–6].
Вопросы для самопроверки
1. Что такое достоверное, невозможное и случайное событие?
2. Как найти вероятность суммы событий?
3. Что такое условная вероятность?
4. Как найти вероятность произведения событий?
5. В чём состоит формула полной вероятности?
6. В чём состоит формула Бейеса?
7. В чём состоит формула Бернулли?
8. Сформулируйте локальную и интегральную теоремы Лапласа.
9. Сформулируйте теорему Пуассона.
Пример 1. В первом ящике находятся 3 белых и 7 чёрных шаров, а во втором – 5 белых и 3 чёрных шара. Из первого ящика переложили во второй два случайным образом выбранных шара. Затем из второго ящика достали один шар. Определить вероятности следующих событий:
1) в первом ящике осталось не более двух белых шаров;
2) шар, извлечённый из второго ящика, оказался белым;
3) шары, переложенные из первого ящика во второй, были разного цвета, если известно, что шар, извлечённый из второго ящика, оказался белым.
Решение
Рассмотрим следующие случайные события:
H1 – из первого ящика переложили во второй 2 белых шара;
H2 – из первого ящика переложили во второй 2 чёрных шара;
H3 – из первого ящика переложили во второй 1 белый и 1 чёрный шар;
B – в первом ящике осталось не более 2 х белых шаров;
С – шар, извлечённый из второго ящика, – белый.
Найдём вероятности событий H1, H2, H3.
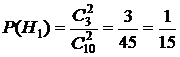 ;
;  ;
; 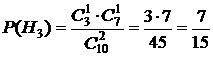 .
.
( ;
; 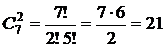 ;
;  ;
; 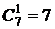 ).
).
1. Событие B состоит в том, что произошло или событие H1 (тогда в первом ящике остался только один белый шар), или событие H3 (при этом в первом ящике осталось два белых шара), т.е. В = H1 + H3. Так как события H1 и H3 несовместны, то
 .
.
2. Для вычисления вероятности события C воспользуемся формулой полной вероятности.
События H1, H2, H3 образуют полную группу событий. Найдём условные вероятности события C:
 ;
; 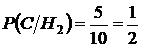 ;
;  .
.
Поэтому
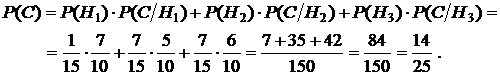
3. В третьем пункте задачи речь идёт о том, что надо найти вероятность события H3 («шары, переложенные во второй ящик, были разного цвета») при условии, что произошло событие C («из второго ящика достали белый шар»), т.е. следует найти 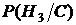 . Эту вероятность найдём по формуле Бейеса:
. Эту вероятность найдём по формуле Бейеса:
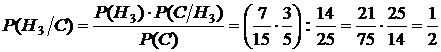 .
.
Пример 2. Вероятность наступления события в каждом из n одинаковых и независимых испытаний равна p. В пунктах а), б) и в) найти вероятность того, что в этих испытаниях событие появится k раз; в пункте г) найти вероятность того, что событие появится не менее a раз и не более b раз.
a) p = 0,45, n = 8, k = 4; б) p = 0,02, n = 300, k = 5;
в) p = 0,7, n = 2100, k = 1500; г) p = 0,375, n = 1375, a = 525, b = 545.
Решение
а) Если вероятность появления события в каждом независимом испытании постоянна и равна p, то вероятность появления события ровно k раз в серии из n испытаний вычисляется по формуле Бернулли
 , где
, где 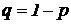 .
.
 .
.
Заметим, что расчёты по формуле Бернулли при больших n достаточны сложны. Поэтому вероятность  находится приближенно.
находится приближенно.
б) Если число независимых испытаний n велико (n > 100), а вероятность p появления события в каждом них мала (p £ 0,3), то для приближенного вычисления вероятности появления события ровно k раз в серии из n испытаний используется формула Пуассона
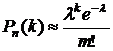 , где
, где 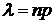 .
.
Условия пункта б) удовлетворяют вышеуказанным требованиям (n = 300 > 100, p = 0,02 < 0,3). Находим 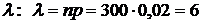 .
.
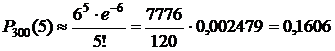 .
.
в) Если n достаточно большое и np ³ 7, то формула Пуассона даёт большую погрешность. В этом случае для вычисления используют локальную теорему Лапласа:
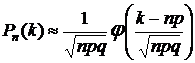 , где
, где 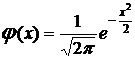 .
.
Функция 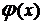 табулирована, её таблицы приведены в приложении учебника [4]. В таблицах помещены значения функции только для положительных значений аргумента х. Для отрицательных значений х использует те же таблицы, так как рассматриваемая функция – чётная.
табулирована, её таблицы приведены в приложении учебника [4]. В таблицах помещены значения функции только для положительных значений аргумента х. Для отрицательных значений х использует те же таблицы, так как рассматриваемая функция – чётная.
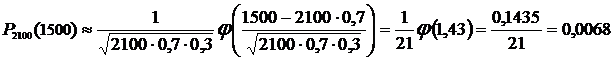 .
.
г) Если нас интересует вероятность, что событие появится не менее a раз и не более b раз при большом n, применяют формулу, которая выражает содержание интегральной теоремы Лапласа:
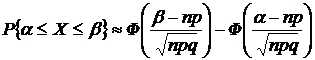 , где F(х)
, где F(х) 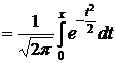
F(x) – функция Лапласа – также табулирована [4]. Уже при x = 5 функция F(x) очень мало отличается от 0,5 (F(5) = 0,499997). Поэтому для всех x > 5 принимается, что F(x) » 0,5. Функция Лапласа – нечётная функция, т.е. F(– x) = – F(x).
В нашем случае
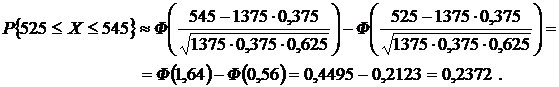
Случайные величины
Литература. [1 гл. 5, гл. 6 §1–3]; [2 гл. II §1, §7, §8, гл. III §1, §2, §4, гл. V §1, §2]; [3 §5]; [4 гл. 4 §1–3, гл. 6 §1–6]; [5 гл. 3].
Вопросы для самопроверки
1. Что такое случайная величина. Приведите примеры.
2. Дайте определение функции распределения случайной величины и укажите её свойства.
3. Сформулируйте определение плотности распределения вероят-ностей и укажите её свойства.
4. Что называется математическим ожиданием случайной величины. Укажите его свойства.
5. Дайте определение дисперсии случайной величины и укажите её свойства.
6. Что такое среднее квадратическое отклонение случайной величины.
7. Дайте описания дискретных и непрерывных распределений: биномиального, пуассоновского, нормального, показательного, равномер-ного.
8. Как найти вероятность попадания случайной величины в заданный интервал, если она распределена по нормальному или показательному закону?
9. Сформулируйте центральную предельную теорему.
Пример 3. Задан закон распределения дискретной случайной величины X. Найти  ,
, 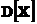 ,
,  и
и 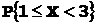 .
.
| X | ||||
| P | 0,1 | 0,2 | 0,3 | 0,4 |
Решение
1. Математическое ожидание  вычисляем по формуле
вычисляем по формуле 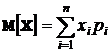 .
.
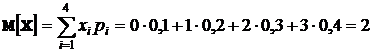 .
.
2. Дисперсию 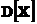 вычисляем по формуле
вычисляем по формуле 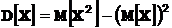 .
.

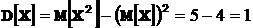 .
.
3. Среднее квадратическое отклонение  .
.
4. Вероятность  .
.
Пример 4. Непрерывная случайная величина X подчинена закону распределения с плотностью  Найти коэффициент а, числовые характеристики
Найти коэффициент а, числовые характеристики  ,
, 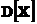 ,
,  , функцию распределения
, функцию распределения 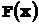 и
и  .
.
Решение
1. Для определения коэффициента а используем свойство плотности распределения 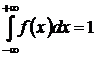 .
.
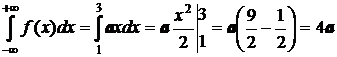 .
. 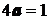 .
.  .
.
2. Функцию распределения 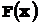 вычисляем по формуле
вычисляем по формуле  .
.
При 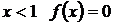 .
. 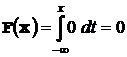
При 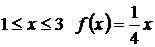 .
. 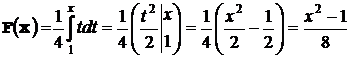 .
.
При 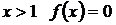 .
. 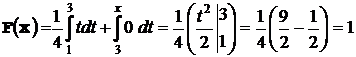 .
.
Таким образом, функция распределения 
3. Математическое ожидание  вычисляем по формуле
вычисляем по формуле  .
.
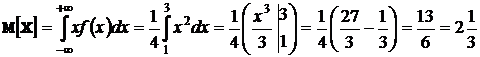 .
.
4. Дисперсию 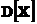 вычисляем по формуле
вычисляем по формуле 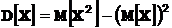 .
.
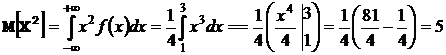 .
.
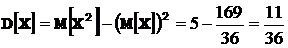 .
.
5. Среднее квадратическое отклонение 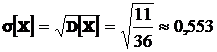 .
.
6. Вероятность попадания на отрезок 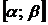 вычисляем по формуле
вычисляем по формуле 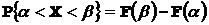 .
.
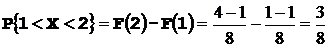 .
.
Пример 5. Случайная величина Х распределена по нормальному закону. Найти среднее квадратическое отклонение случайной величины Х и вероятность 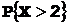 , если известно, что
, если известно, что 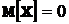 и
и 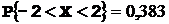 .
.
Решение
Для случайной величины X, распределенной по нормальному закону с параметрами a и s,  , где Ф(x) – функция Лапласа.
, где Ф(x) – функция Лапласа.
 ;
; 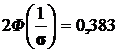 ;
;
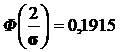 ; по таблице функции Ф(x) находим, что
; по таблице функции Ф(x) находим, что 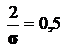 ;
; 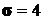 .
.
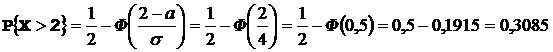 .
.
После изучения темы XIX выполните контрольную работу № 7.
Тема XX. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ЭЛЕМЕНТЫМАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Двумерные случайные величины
Литература. [1 гл. 8 §1, §2, §4, §6]; [2 гл. VI §1, гл. IX §1, §2]; [4 гл. 8 §1–3, гл. 12 §1]; [5 гл. 3 §9, гл. 10 §1, §2].
Вопросы для самопроверки
1. Как задаётся закон распределения двумерной дискретной случайной величины?
2. Как определяются законы распределения составляющих, если известен закон распределения двумерной случайной величины?
3. Что такое корреляционный момент? Что такое коэффициент корреляции? Укажите свойства коэффициента корреляции.
4. Как определяются условные законы распределения случайных величин по заданному закону распределения двумерной случайной величины?
5. Как в общем случае ставится задача отыскания функции регрессии случайной величины X на случайную величину Y (случайной величины Y на случайную величину X)?
6. Как записывается уравнение средней квадратической регрессии случайной величины в классе линейных функций?
Пример 6. Найти уравнения прямой линии средней квадратической регрессии случайной величины Y на случайную величину Х и случайной величины Х на случайную величину Y по заданному закону двумерной случайной величины 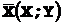 :
:
| X Y | ||||
| 0,1 | 0,1 | 0,25 | ||
| 0,1 | 0,2 | |||
| 0,1 | 0,15 |
Решение
Уравнение средней квадратической регрессии случайной величины Y на случайную величину Х в классе линейных функций имеет вид:
 .
.
Для нахождения числовых характеристик  ,
,  ,
,  ,
, 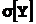 восстановим по заданному закону двумерной величины
восстановим по заданному закону двумерной величины 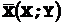 законы распределения составляющих X и Y.
законы распределения составляющих X и Y.
| X | Y | ||||||||
| P | 0,2 | 0,2 | 0,4 | 0,2 | P | 0,45 | 0,3 | 0,25 |
Математические ожидания  и
и  вычисляем по формулам
вычисляем по формулам
 .
.
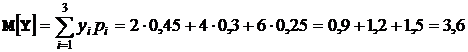 .
.
Для нахождения средних квадратических отклонений  и
и 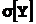 сначала вычисляем дисперсии
сначала вычисляем дисперсии 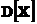 ,
,  .
.
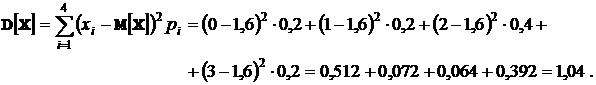
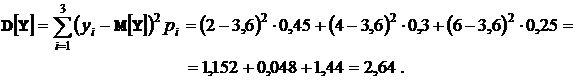
Следовательно,  .
.
Коэффициент корреляции 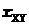 вычисляем по формуле
вычисляем по формуле  ,
,
где 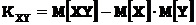 – корреляционный момент случайной величины
– корреляционный момент случайной величины 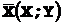 .
.
 .
.
 .
. 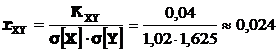 .
.
Подставляя найденные числовые характеристики в формулу, получаем уравнение прямой линии средней квадратической регрессии случайной величины Y на случайную величину Х.
 или
или 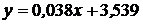 .
.
Уравнение средней квадратической регрессии случайной величины X на случайную величину Y в классе линейных функций имеет вид:
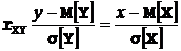 .
.
Подставляя найденные числовые характеристики, получаем следующее уравнение прямой линии регрессии X на Y
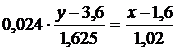 или
или 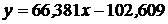 .
.