Литература. [1 гл. 7 §1–4]; [2 гл. X, гл. XI §1, §2]; [3 § 12, § 14];
[4 гл. 9, гл. 10 §1, §4, гл. 13 §16]; [5 гл. 5 §3, §8–12, гл. 6 §1, §5].
Вопросы для самопроверки
1. Что называется выборкой? Что такое выборочное среднее?
2. В каком случае выборочная оценка статистического параметра будет называться несмещенной?
3. Что такое выборочная дисперсия? Какова несмещённая оценка для дисперсии?
4. Что называется доверительным интервалом для параметра распределения случайной величины?
5. Как найти доверительный интервал для математического ожидания нормальной случайной величины?
6. Как найти доверительный интервал для дисперсии нормальной случайной величины?
7. Что такое статистическая гипотеза?
8. Какова общая схема проверки статистических гипотез?
9. В чём состоит критерий c2 (Пирсона) для проверки статистической гипотезы?
Пример 7. В результате независимых испытаний получены 50 значений непрерывной случайной величины Х.
1. Нàéòè íåсмещённые оценки математического ожидания  и дисперсии
и дисперсии 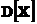 .
.
2. Предполагая, что случайная величина Х распределена по нормальному закону, найти:
а) доверительные интервалы для  , соответствующие доверительным вероятностям 0,95 и 0,9;
, соответствующие доверительным вероятностям 0,95 и 0,9;
б) доверительные интервалы для 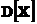 , соответствующие доверительным вероятностям 0,95 и 0,9.
, соответствующие доверительным вероятностям 0,95 и 0,9.
3. Проверить гипотезу о том, что случайная величина Х распределена по нормальному закону. Для проверки гипотезы использовать критерий c2 (Пирсона) при уровнях значимости 0,05 и 0,01.
| 8,3 | 3,8 | 3,6 | 4,8 | 2,9 | 3,2 | 7,4 | 2,5 | 3,5 | –2,9 |
| 3,2 | 5,6 | 3,3 | 3,4 | 0,7 | 3,3 | –1,7 | 1,7 | –1,8 | 3,4 |
| 0,1 | 8,2 | –1,6 | 2,4 | 4,5 | 7,2 | 3,1 | –0,3 | 2,4 | 2,0 |
| 1,7 | –3,3 | 6,3 | 3,1 | 3,9 | 2,0 | 4,5 | –0,2 | 5,5 | 7,0 |
| 1,9 | 5,7 | 1,3 | 2,2 | 5,2 | 5,1 | –0,9 | 6,8 | 2,2 | –2,6 |
Решение
1. Несмещённой оценкой  является выборочное среднее
является выборочное среднее  .
.
 .
.
Несмещённой оценкой 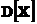 является статистика
является статистика  .
.
 .
.
2. Доверительный интервал для  , соответствующий доверительной вероятности b, имеет вид
, соответствующий доверительной вероятности b, имеет вид  , где число
, где число  находится с помощью таблиц распределения Стьюдента с
находится с помощью таблиц распределения Стьюдента с  степенями свободы из условия
степенями свободы из условия  [4].
[4].
Доверительной вероятности  и числу степеней свободы 49 соответствует
и числу степеней свободы 49 соответствует  . Подставляя в формулу, получаем следующий доверительный интервал для
. Подставляя в формулу, получаем следующий доверительный интервал для  , соответствующий
, соответствующий  :
:  .
.
Доверительной вероятности  и числу степеней свободы 49 соответствует
и числу степеней свободы 49 соответствует  . Подставляя в формулу, получаем следующий доверительный интервал для
. Подставляя в формулу, получаем следующий доверительный интервал для  , соответствующий
, соответствующий  :
: 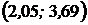 .
.
Доверительный интервал для 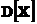 , соответствующий доверительной вероятности b, имеет вид
, соответствующий доверительной вероятности b, имеет вид  , где число
, где число  находится с помощью таблиц стандартного нормального распределения из условия
находится с помощью таблиц стандартного нормального распределения из условия  .
.
Доверительной вероятности  соответствует
соответствует  . Подставляя в формулу, получаем следующий доверительный интервал для
. Подставляя в формулу, получаем следующий доверительный интервал для 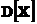 , соответствующий
, соответствующий  :
:  .
.
Доверительной вероятности  соответствует
соответствует  . Подставляя в формулу, получаем следующий доверительный интервал для
. Подставляя в формулу, получаем следующий доверительный интервал для 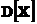 , соответствующий
, соответствующий  :
:  .
.
3. Для проверки гипотезы интервал возможных значений 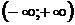 случайной величины Х разбиваем на 5 промежутков. Границы промежутков определяются равенствами
случайной величины Х разбиваем на 5 промежутков. Границы промежутков определяются равенствами
 ,
,
где  – квантиль стандартного нормального распределения (квантиль
– квантиль стандартного нормального распределения (квантиль  определяется равенством
определяется равенством 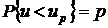 ).
).
В частности  .
.
Подставляя  в формулы, получаем следующие границы промежутков:
в формулы, получаем следующие границы промежутков:  .
.
Подсчитаем число выборочных значений  в каждом из промежутков
в каждом из промежутков  : n 1 = 10; n 2 = 7; n 3 = 16; n 4 = 7; n 5 = 10.
: n 1 = 10; n 2 = 7; n 3 = 16; n 4 = 7; n 5 = 10.
Вычисляем значение 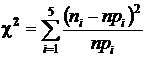 , где n = 50,
, где n = 50,  ,
,  – число выборочных значений в i- ом промежутке.
– число выборочных значений в i- ом промежутке.
 .
.
Сравниваем вычисленное значение c2 с критическим значением  , найденным с помощью таблиц c2 –распределения по заданному уровню значимости e и числу степеней свободы 2.
, найденным с помощью таблиц c2 –распределения по заданному уровню значимости e и числу степеней свободы 2.
Уровню значимости e = 0,01 и числу степеней свободы 2 соответствует  . Так как c2 <
. Так как c2 <  (5,4 < 9,2), то на уровне значимости e = 0,01 отвергнуть гипотезу о том, что случайная величина X распределена по нормальному закону, нет оснований.
(5,4 < 9,2), то на уровне значимости e = 0,01 отвергнуть гипотезу о том, что случайная величина X распределена по нормальному закону, нет оснований.
Уровню значимости e = 0,05 и числу степеней свободы 2 соответствует  . Так как c2 <
. Так как c2 <  (5,4 < 6,0), то на уровне значимости e = 0,05 отвергнуть гипотезу о том, что случайная величина X распределена по нормальному закону, нет оснований.
(5,4 < 6,0), то на уровне значимости e = 0,05 отвергнуть гипотезу о том, что случайная величина X распределена по нормальному закону, нет оснований.
После изучения темы XX выполните контрольную работу № 8.
Ниже приведена таблица номеров задач, входящих в две контрольные работы, которые выполняются студентами в четвёртом семестре. Студент должен выполнить контрольные задания по варианту, номер которого совпадает с последней цифрой его учебного номера (шифра).
| Вариант | Номера задач контрольных заданий | ||||||
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ
1. В первом ящике находятся 7 белых и 3 чёрных шара, а во втором – 2 белых и 3 чёрных шара. Из первого ящика выбирают случайным образом один шар и перекладывают его во второй ящик. Затем из второго ящика один шар перекладывают в первый ящик. После этой процедуры из первого ящика извлекают один шар. Определить вероятности следующих событий:
1) число белых шаров во втором ящике не изменилось;
2) шар, извлечённый из первого ящика, оказался белым;
3) число белых шаров во втором ящике увеличилось, если известно, что шар, извлечённый из первого ящика, оказался белым.
2. В первом ящике находятся 1 белый и 9 чёрных шаров, а во втором – 2 белых и 9 чёрных шаров. Из каждого ящика случайным образом извлекли по два шара и положили в третий ящик. Затем из третьего ящика достали один шар. Определить вероятности следующих событий:
1) во втором ящике остался хотя бы один белый шар;
2) шар, извлечённый из третьего ящика, оказался чёрным;
3) в первом и втором ящиках осталось ровно по одному белому шару, если известно, что шар, извлечённый из третьего ящика, оказался чёрным.
3. В ящике находятся 3 белых и 7 красных шаров. Случайным образом из ящика извлекаются два шара. Если хотя бы один из них окажется белым, то их возвращают в ящик и добавляют дополнительно ещё 2 белых шара. Если же извлечённые шары окажутся красными, то их удаляют из ящика. Пусть процедура была проведена один раз. Затем из ящика достали один шар. Определить вероятности следующих событий:
1) в ящике находится более десяти шаров;
2) шар, изъятый из ящика, оказался белым;
3) в ящике осталось не более десяти шаров, если известно, что шар, изъятый из ящика, оказался белым.
4. В первом ящике находятся 2 белых и 5 чёрных шаров, а во втором – 1 белый и 6 чёрных шаров. Из каждого ящика удалили по два шара, а оставшиеся шары ссыпали в третий ящик. Затем из третьего ящика достали один шар. Определить вероятности следующих событий:
1) среди удалённых шаров будет не менее двух белых;
2) шар, извлечённый из третьего ящика, оказался белым;
3) в третьем ящике находятся девять чёрных шаров, если известно, что шар, извлечённый из третьего ящика, оказался белым.
5. В первом ящике находятся 2 белых и 6 красных шаров, а во втором – 2 белых и 8 красных шаров. Из второго ящика переложили в первый два случайным образом выбранных шара. Затем из первого ящика достали один шар. Определить вероятности следующих событий:
1) хотя бы один из шаров, добавленных в первый ящик, был красным;
2) шар, извлечённый из первого ящика, оказался красным;
3) во втором ящике осталось два белых шара, если известно, что шар, извлечённый из первого ящика, оказался красным.
6. В каждом из трёх ящиков находятся 1 белый и 2 чёрных шара. Из первого ящика случайным образом выбрали один шар и переложили во второй, тщательно перемешали шары, а затем переложили один шар из второго ящика в третий. Определить вероятности следующих событий:
1) в третьем ящике будет два белых шара;
2) шар, взятый наугад из третьего ящика, окажется белым;
3) в третий ящик был добавлен белый шар, если известно, что шар, взятый наугад из третьего ящика, оказался белым.
7. В первом ящике находятся 2 белых и 3 красных шара, а во втором – 6 белых и 4 красных шара. В случайно выбранный ящик добавили 2 красных шара. Затем из выбранного наудачу ящика по очереди (без возвращения) достают два шара. Определить вероятности следующих событий:
1) первый из выбранных шаров будет красным;
2) хотя бы один из выбранных шаров будет красным;
3) шары выбирались из первого ящика, если известно, что первый из выбранных шаров был красным.
8. В первом ящике находятся 4 белых и 2 чёрных шара, а во втором – 1 белый и 5 чёрных шаров. Из первого ящика переложили во второй два случайным образом выбранных шара. Затем из второго ящика достали один шар. Определить вероятности следующих событий:
1) среди шаров, отобранных из первого ящика, будет хотя бы один белый;
2) шар, извлечённый из второго ящика, оказался белым;
3) шары, переложенные из первого ящика во второй, были разного цвета, если известно, что шар, извлечённый из второго ящика, оказался белым.
9. Из первого ящика, содержащего 6 белых и 2 чёрных шара, отобрали наудачу два шара, а из второго ящика, содержащего 3 белых и 2 чёрных шара, отобрали один шар. Отобранные шары положили в пустой третий ящик. Затем из третьего ящика достали один шар. Определить вероятности следующих событий:
1) в первом ящике остался хотя бы один чёрный шар;
2) шар, извлечённый из третьего ящика, оказался белым;
3) в первом ящике остались только белые шары, если известно, что шар, извлечённый из третьего ящика, оказался белым.
10. В первом ящике находятся 6 белых и 2 чёрных шара, а во втором – 3 белых и 5 чёрных шаров. В случайно выбранный ящик добавили 1 белый и 1 чёрный шар. Затем из каждого ящика достали по одному шару. Определить вероятности следующих событий:
1) из первого ящика достали белый шар;
2) выбранные шары оказались разного цвета;
3) шары были добавлены в первый ящик, если известно, что из первого ящика достали белый шар.
№№11–20. Вероятность появления события в каждом из n одинаковых и независимых испытаний равна p. В пунктах а), б) и в) найти вероятность того, что в этих испытаниях событие появится k раз; в пункте г) найти вероятность того, что событие появится не менее a раз и не более b раз.
11. a) p = 0,1, n = 7, k = 3; б) p = 0,002, n = 1000, k = 3;
в) p = 0,2, n = 320, k = 60; г) p = 0,7, n = 730, a = 500, b = 520.
12. a) p = 0,3, n = 4, k = 2; б) p = 0,025, n = 160, k = 5;
в) p = 0,9, n = 610, k = 550; г) p = 0,4, n = 490, a = 205, b = 216.
13. a) p = 0,5, n = 6, k = 3; б) p = 0,006, n = 500, k = 4;
в) p = 0,4, n = 460, k = 180; г) p = 0,6, n = 810, a = 480, b = 510.
14. a) p = 0,7, n = 5, k = 2; б) p = 0,001, n = 4000, k = 3;
в) p = 0,7, n = 515, k = 355; г) p = 0,35, n = 670, a = 220, b = 250.
15. a) p = 0,9, n = 7, k = 4; б) p = 0,01, n = 200, k = 6;
в) p = 0,6, n = 840, k = 495; г) p = 0,5, n = 520, a = 270, b = 330.
16. a) p = 0,9, n = 5, k = 3; б) p = 0,015, n = 400, k = 2;
в) p = 0,3, n = 280, k = 90; г) p = 0,8, n = 430, a = 340, b = 390.
17. a) p = 0,8, n = 6, k = 2; б) p = 0,008, n = 375, k = 3;
в) p = 0,5, n = 450, k = 215; г) p = 0,65, n = 650, a = 410, b = 440.
18. a) p = 0,6, n = 7, k = 5; б) p = 0,0025, n = 800, k = 5;
в) p = 0,8, n = 720, k = 570; г) p = 0,9, n = 305, a = 270, b = 280.
19. a) p = 0,4, n = 4, k = 1; б) p = 0,002, n = 2000, k = 4;
в) p = 0,35, n = 340, k = 110; г) p = 0,45, n = 770, a = 340, b = 360.
20. a) p = 0,2, n = 6, k = 4; б) p = 0,004, n = 1250, k = 3;
в) p = 0,65, n = 660, k = 435; г) p = 0,3, n = 450, a = 130, b = 190.
№№21–30. Задан закон распределения дискретной случайной величины X. Найти числовые характеристики M[X], D[X], s[X] и P{a£X<b}. Построить график функции распределения случайной величины Х.
21.
| X | –3 | –2 | a =–2 | |||
| P | 0,15 | 0,3 | 0,1 | 0,2 | 0,25 | b = 2 |
22.
| X | a = 0 | |||||
| P | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 | b = 3 |
23.
| X | a = 2 | |||||
| P | 0,38 | 0,26 | 0,2 | 0,14 | 0,02 | b = 5 |
24.
| X | –4 | –3 | –2 | –1 | a =–4 | |
| P | 0,25 | 0,2 | 0,1 | 0,2 | 0,25 | b = 0 |
25.
| X | –1,5 | –1 | 1,5 | a =–1 | ||
| P | 0,1 | 0,2 | 0,25 | 0,25 | 0,2 | b = 1 |
26.
| X | a = 2 | |||||
| P | 0,2 | 0,3 | 0,3 | 0,1 | 0,1 | b = 5 |
27.
| X | –2 | –0,5 | 0,5 | a =–0,5 | ||
| P | 0,1 | 0,1 | 0,6 | 0,1 | 0,1 | b = 0,5 |
28.
| X | –1 | a = 0 | ||||
| P | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 | b = 3 |
29.
| X | –4 | –1 | a =–4 | |||
| P | 0,05 | 0,2 | 0,2 | 0,35 | 0,2 | b = 1 |
30.
| X | –2 | a = 1 | ||||
| P | 0,15 | 0,05 | 0,5 | 0,1 | 0,2 | b = 4 |
№№31–40. Непрерывная случайная величина X подчинена закону распределения с плотностью f(x). Найти коэффициент а, функцию распределения F(x), числовые характеристики M[X], D[X], s[X] и вероятности p 1, p 2, p 3.
31.

| p1 = P{X £ 0}; p2 = P{1 < X £ 5}; p3 = P{X > 0,5}. |
32.

| p1 = P{X £ 3}; p2 = P{2 < X < 5}; p3 = P{X > 3,5}. |
33.

| p1 = P{X £ 2,5}; p2 = P{3 £ X < 7}; p3 = P{X > 3,5}. |
34.

| p1 = P{X < 3}; p2 = P{0 £ X < 7}; p3 = P{X > 4}. |
35.

| p1 = P{X < –0,5}; p2 = P{–6 < X £ –1}; p3 = P{X > 0,5}. |
36.

| p1 = P{X £ 4}; p2 = P{2,5 < X < 7}; p3 = P{X > 3}. |
37.

| p1 = P{X £ 3}; p2 = P{2,5 < X < 3,5}; p3 = P{X > 4}. |
38.

| p1 = P{X < 5}; p2 = P{3 < X < 10}; p3 = P{X ³ 5,5}. |
39.

| p1 = P{X < 0}; p2 = P{–1 < X < 5}; p3 = P{X ³ 1}. |
40.

| p1 = P{X £ –0,5}; p2 = P{–5 £ X £ 2}; p3 = P{X ³ 1}. |
41. Случайная величина Х распределена по нормальному закону. Найти математическое ожидание и дисперсию случайной величины X, если известно, что  и
и  .
.
42. Случайная величина Х распределена по нормальному закону, причём D[X]=25. Найти M[X] и d, если известно, что  и
и  .
.
43. Случайная величина Х распределена по нормальному закону. Найти математическое ожидание и дисперсию случайной величины X, если известно, что  и
и  .
.
44. Случайная величина Х распределена по нормальному закону. Найти математическое ожидание и дисперсию случайной величины X, если известно, что  и
и  .
.
45. Случайная величина Х распределена по нормальному закону, причём М[X]=1. Найти среднее квадратическое отклонение случайной величины Х и  , если известно, что
, если известно, что  .
.
46. Случайная величина Х распределена по нормальному закону. Найти математическое ожидание и дисперсию случайной величины X, если известно, что  и
и  .
.
47. Случайная величина Х распределена по нормальному закону. Найти математическое ожидание и дисперсию случайной величины X, если известно, что  и
и  .
.
48. Случайная величина Х распределена по нормальному закону, причём D[X]=25. Найти M[X] и  , если известно, что
, если известно, что  .
.
49. Случайная величина Х распределена по нормальному закону. Найти M[X], D[X] и  , если известно, что
, если известно, что  и
и  .
.
50. Случайная величина Х распределена по нормальному закону, причём s [X]=0,5. Найти M[X],  и
и  , если известно, что
, если известно, что  .
.
№№51–60. Найти уравнения прямой линии средней квадратической регрессии случайной величины Y на случайную величину Х и случайной величины Х на случайную величину Y по заданному закону двумерной случайной величины  :
:
| Y X | y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 |
| x1 | 0,01 | 0,02 | 0,04 | |||||
| x2 | 0,01 | 0,03 | 0,06 | 0,02 | ||||
| x3 | 0,04 | 0,06 | 0,08 | 0,02 | ||||
| x4 | 0,02 | 0,06 | 0,08 | 0,03 | 0,01 | |||
| x5 | 0,01 | 0,04 | 0,12 | 0,10 | 0,01 | |||
| x6 | 0,01 | 0,06 | 0,04 | 0,02 |
Построить графики полученных линейных функций и точки  для i = 1, 2,¼, 6. Значения случайных величин X и Y взять из соответствующих таблиц согласно номеру варианта.
для i = 1, 2,¼, 6. Значения случайных величин X и Y взять из соответствующих таблиц согласно номеру варианта.
| 51. | x1 | x2 | x3 | x4 | x5 | x6 |
| 1,2 | 1,4 | 1,6 | 1,8 |
| y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | |
| 52. | x1 | x2 | x3 | x4 | x5 | x6 |
| 2,4 | 2,8 | 3,2 | 3,6 |
| y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | |||||
| 53. | x1 | x2 | x3 | x4 | x5 | x6 | ||||||
| 3,6 | 4,2 | 4,8 | 5,4 | |||||||||
| y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | |
| 54. | x1 | x2 | x3 | x4 | x5 | x6 |
| 4,8 | 5,6 | 6,4 | 7,2 |
| y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | |
| 55. | x1 | x2 | x3 | x4 | x5 | x6 |
| y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | |
| 56. | x1 | x2 | x3 | x4 | x5 | x6 |
| 7,2 | 8,4 | 9,6 | 10,8 |
| y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | |
| 57. | x1 | x2 | x3 | x4 | x5 | x6 |
| 8,4 | 9,8 | 11,2 | 12,6 |
| y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | |
| 58. | x1 | x2 | x3 | x4 | x5 | x6 |
| 9,6 | 11,2 | 12,8 | 14,4 |
| y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | |
| 59. | x1 | x2 | x3 | x4 | x5 | x6 |
| 10,8 | 12,6 | 14,4 | 16,2 |
| y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | |
| 60. | x1 | x2 | x3 | x4 | x5 | x6 |
| y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | |
№№61–70. В результате независимых испытаний получены 50 значений непрерывной случайной величины Х.
1. Найти несмещённые оценки математического ожидания M[X] и дисперсии D[X].
2. Предполагая, что случайная величина Х распределена по нормальному закону, найти:
а) доверительные интервалы для M[X], соответствующие доверительным вероятностям 0,95 и 0,9;
б) доверительные интервалы для D[X], соответствующие доверительным вероятностям 0,95 и 0,9.
3. Проверить гипотезу о том, что случайная величина Х распределена по нормальному закону. Для проверки гипотезы использовать критерий c2 (Пирсона) при уровнях значимости 0,05 и 0,01.
| 61. | 3,4 | 2,6 | –1,3 | 7,6 | 7,0 | 0,5 | 2,7 | 5,5 | 7,4 | 1,2 |
| 4,2 | 8,8 | 6,6 | –0,4 | 3,7 | 4,0 | 6,0 | 5,1 | 2,7 | 2,6 | |
| 0,4 | 2,7 | 5,9 | 0,7 | 3,9 | 6,8 | 3,9 | 2,2 | 7,4 | –1,5 | |
| 5,8 | 6,4 | 2,1 | –1,2 | 3,8 | 6,4 | –1,9 | 1,6 | 7,1 | 2,7 | |
| 1,2 | 2,5 | 8,4 | 6,1 | 3,3 | 1,3 | –0,3 | 0,9 | 3,0 | –0,1 |
| 62. | –0,4 | –0,5 | –1,2 | –1,4 | –1,0 | 6,0 | 6,2 | –1,9 | 8,6 | 5,9 |
| 1,7 | 2,5 | 7,9 | 4,6 | 1,2 | 8,9 | 6,1 | 1,2 | –2,9 | 5,3 | |
| 1,4 | 2,2 | 0,5 | 0,9 | 1,1 | 6,4 | 5,7 | 1,8 | 6,6 | –2,0 | |
| 0,1 | 7,9 | 1,0 | 6,5 | 6,5 | 0,1 | –0,1 | 6,3 | 5,7 | 7,4 | |
| 0,8 | 5,6 | –0,9 | 3,5 | 6,0 | 2,1 | –1,9 | 0,9 | –0,6 | 7,2 |
| 63. | 6,0 | 6,6 | 0,9 | 6,0 | 5,6 | 2,2 | 6,6 | 2,6 | 5,0 | 6,5 |
| 1,6 | 1,3 | 5,8 | 2,9 | 4,2 | 7,2 | 2,6 | 2,3 | 7,8 | 2,6 | |
| 4,3 | 3,2 | 6,5 | 6,1 | 1,0 | 0,2 | 7,3 | 1,1 | 2,7 | 7,1 | |
| 3,7 | 0,4 | 4,4 | 8,2 | 3,4 | –1,5 | 6,0 | 7,6 | 4,5 | 6,2 | |
| 7,6 | 7,3 | –2,4 | 7,6 | 0,8 | –0,4 | 3,8 | 8,0 | 0,1 | 6,2 |
| 64. | 4,8 | –2,6 | 5,1 | 7,3 | –0,4 | 8,3 | 1,5 | 8,0 | –1,4 | 1,6 |
| 5,4 | 4,9 | 5,6 | 7,0 | 6,8 | 1,2 | 3,8 | –0,9 | 8,1 | 6,4 | |
| 3,9 | 1,8 | 2,2 | 0,8 | 6,0 | 5,8 | 1,0 | –1,6 | 5,7 | –1,4 | |
| –0,4 | 4,8 | 1,6 | 0,8 | –0,8 | –1,4 | 3,9 | 9,1 | –1,3 | 3,6 | |
| –1,6 | –0,5 | 1,8 | 2,8 | –2,4 | 4,3 | 6,1 | 3,6 | 0,7 | 3,2 |
| 65. | 3,6 | 4,6 | –2,0 | 3,5 | 6,4 | 7,8 | –0,5 | 2,8 | 4,2 | 8,3 |
| –2,1 | 5,9 | 1,0 | 2,9 | 5,5 | –0,1 | 3,9 | –2,3 | –2,6 | 4,5 | |
| 4,7 | –0,9 | 2,7 | 4,9 | 4,8 | 1,8 | 0,7 | 3,1 | 5,1 | 3,4 | |
| 3,2 | 3,0 | 1,3 | 1,0 | –0,9 | 0,9 | 8,0 | 7,1 | –0,7 | 2,4 | |
| 8,6 | 7,1 | 6,4 | 0,7 | 0,2 | –0,5 | 7,1 | 0,2 | 2,2 | 5,9 |
| 66. | 8,5 | 2,6 | –1,1 | 1,7 | 6,1 | –0,7 | 1,1 | 5,3 | 8,3 | 3,0 |
| 4,1 | 2,1 | 3,8 | 4,6 | 0,9 | 1,8 | –1,3 | 10,1 | –2,4 | 4,1 | |
| 1,7 | –1,4 | 0,7 | –0,8 | 6,8 | 2,7 | 5,6 | –0,7 | 3,4 | 3,4 | |
| 0,1 | 2,8 | 5,4 | –0,2 | 3,4 | –0,7 | –0,8 | 6,9 | –2,0 | –1,1 | |
| 1,1 | 4,5 | 7,7 | 7,7 | –1,2 | 8,2 | 8,2 | 5,6 | 2,2 | 1,6 |
| 67. | 0,4 | 5,1 | 6,4 | 8,2 | 1,2 | –1,7 | 0,6 | 1,6 | –0,1 | 1,9 |
| 0,9 | 3,2 | 7,7 | 0,5 | 5,5 | 6,0 | 4,0 | 2,1 | 2,8 | 0,2 | |
| 2,1 | 6,5 | 0,8 | 5,5 | 8,8 | 3,2 | 2,7 | 0,2 | 7,6 | 3,4 | |
| 5,8 | 2,2 | 6,2 | 3,8 | 1,8 | 3,0 | 3,6 | 0,9 | 8,2 | 7,7 | |
| 4,5 | 5,3 | 2,2 | 3,9 | 5,6 | 8,1 | 3,0 | 2,9 | 4,9 | 5,5 |
| 68. | 5,6 | –0,6 | 3,1 | 4,1 | –0,7 | 4,4 | 3,7 | 3,7 | 0,6 | 4,6 |
| 1,0 | 0,3 | 7,6 | 7,5 | 5,4 | 8,0 | 5,8 | 7,3 | 6,2 | 7,7 | |
| 5,2 | –1,2 | 3,1 | 5,3 | 5,9 | 8,4 | 1,3 | 1,5 | 4,6 | 6,7 | |
| –0,6 | 5,3 | 2,4 | 4,3 | –3,2 | 2,5 | 1,0 | 6,6 | –0,5 | 0,5 | |
| 2,6 | 0,6 | 3,1 | –1,8 | 6,8 | 1,8 | –1,8 | 0,1 | 3,7 | 3,4 |
| 69. | 5,8 | 0,4 | 7,7 | 7,2 | 5,6 | 1,7 | 3,6 | –3,0 | 3,7 | 5,7 |
| 3,5 | 4,5 | 2,2 | 1,1 | –0,5 | 4,0 | 3,8 | 6,9 | –1,7 | 2,7 | |
| 6,7 | 7,2 | 1,5 | 0,4 | 4,2 | 5,0 | –0,5 | 4,0 | –0,7 | –1,5 | |
| –0,7 | 1,4 | 1,2 | 5,2 | 6,0 | 0,1 | 5,7 | 0,4 | 3,9 | 3,2 | |
| 0,8 | 2,5 | 3,5 | –3,0 | 5,7 | –0,4 | 6,4 | 7,3 | 7,0 | 4,9 |
| 70. | 5,9 | 4,9 | 0,9 | 5,5 | 4,5 | 5,9 | 6,7 | 1,4 | 1,2 | 8,7 |
| 9,1 | 7,2 | 9,8 | –0,8 | 5,5 | –3,4 | –0,2 | 1,6 | 4,0 | 5,2 | |
| –0,8 | 5,5 | 7,3 | 4,2 | –1,7 | 1,1 | 3,2 | 4,8 | –1,9 | 1,7 | |
| 4,1 |
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2018-01-27 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд