Цель работы: изучение скользящего режима движения, исследование режима слежения в оптимальных по быстродействию системах автоматического регулирования.
Теоретические сведения.
Определение скользящего режима.
В системах, имеющих разрывные нелинейности, может возникнуть особый вид движения, называемый скользящим режимом. Так как нас интересует скользящий режим движения в оптимальной системе, то мы дадим определение скользящего режима и рассмотрим условия его возникновения применительно к релейной системе.
Рассмотрим автономную релейную систему второго порядка, структурная схема которой изображена на рис. 1.
Рис. 1.
Движение такой системы задается уравнениями:
или системой уравнений:
(1)
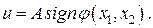(2)
Уравнение
(3)
определяет в фазовом пространстве системы некоторую линию, которую будем называть линией переключения. Действительно, как следует из (2), по одну сторону от этой линии управление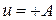 
, а по другую 
(рис. 2).
Рис. 2.
Предположим, что выше линии переключения функция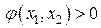 
, а ниже линии 
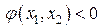. Линия (3), таким образом, разделяет фазовое пространство на две области, одна из которых характеризуется управлением 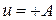, а другая – управлением . Обозначим эти области соответственно 
и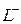 
.
Пусть фазовая точка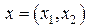 
системы (1) лежит на линии переключения (3). На линии (3) значение управления u не определено. Однако лежащую на линии переключения точку x можно рассматривать как предельную сверху либо снизу. Предположим, что вектор фазовой скорости (точка x лежит на линии (3))
при направлен из области 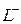в область (рис. 2), а вектор фазовой скорости при 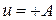направлен из области в область 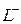. Напомним, что вектор фазовой скорости указывает направление движения фазовой точки. Если указанное выше свойство выполняется в каждой точке линии переключения, то фазовая точка, однажды попав на линию переключения, не может ее покинуть. 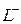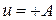Действительно, управление выжимает фазовую точку из области в область , а управление , наоборот, из области в область .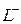
|
|
В любой реальной физической системе имеет место определенное запаздывание в переключении управления. Это приводит к тому, что под воздействием управления фазовая точка пересекает линию (3) и внедряется в область . По истечении времени запаздывания происходит переключение управления с минуса на плюс, а управление 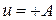выводит фазовую точку из области . В силу запаздывания в переключении управления происходит внедрение фазовой точки в область 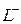и т.д. Движение при этом носит колебательный характер вокруг линии переключения (рис. 3).
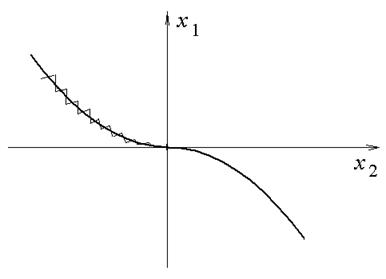
Рис. 3.
Если считать, что запаздывание отсутствует, то частота этих колебаний будет бесконечной, а амплитуда – равной нулю. Такой идеальный случай движения, который характеризуется бесконечной частотой переключения релейного элемента, называется скользящим режимом.
Таким образом, если имеет место скользящий режим движения, то фазовые траектории системы примыкают к линии переключения (линии разрыва), как показано на рис. 4.
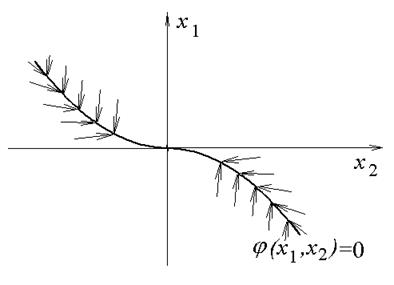
Рис. 4.
Остановимся на получении условий существования скользящего режима в аналитической форме. Проведем в точке x (рис. 2) вектор, ортогональный к линии переключения (3). Таким вектором является вектор
.
Напомним, что вектор 
всегда направлен из области 
в область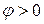 
. Очевидно, для того, чтобы в точке x существовал скользящий режим, необходимо, чтобы вектор фазовой скорости 
составлял с вектором острый угол, а вектор 
- тупой угол. Перемножив векторы скалярно, найдем:
|
|
(4)
В условиях (4) появление знака равенства объясняется тем, что между каждой парой перемножаемых векторов допускается в качестве предельного прямой угол. Используя определение скалярного произведения, неравенства (4) можно переписать в виде:
(5)
Итак, для того, чтобы на линии переключения (3) имел место скользящий режим движения, необходимо, чтобы в каждой точке этой линии выполнялись условия (5). Условия (5) являются необходимыми условиями существования скользящего режима. Нетрудно видеть, что если в (5) исключить знаки равенства, т.е. перейти к строгим неравенствам, то мы получим достаточные условия существования скользящего режима.
Отметим, что условия существования скользящего режима (5) можно получить по структурной схеме рис. 1 или по системе уравнений (1), (2), не прибегая к приведенной выше геометрической интерпретации. Очевидно, фазовая точка 
не может покинуть линии переключения (3), если производная
,
вычисленная в силу уравнений движения (1), будет положительной (неотрицательной) при и отрицательной (неположительной) при 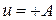. Если сформулированное условие записать в виде формул, то мы получим соотношение (5).
Предположим, что на линии переключения (3) выполняются условия существования скользящего режима. Это означает, что фазовая точка, попав на линию (3), не может покинуть этой линии, т.е. в процессе движения должно выполняться условие (3). Но равенство (3), учитывая уравнения (1), (2), можно переписать в виде:
|
|
. (7)
Уравнение (7) представляет собой дифференциальное уравнение. Это уравнение и определяет движение системы в скользящем режиме. Интересно отметить, что в уравнение (7) не входят параметры объекта (1), т.е. движение в скользящем режиме (до тех пор, пока он существует) инвариантно к изменению параметров объекта (1).
Рассмотрим неавтономную систему n -го порядка. Пусть движение такой системы задается уравнениями:
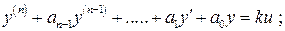(8)
, (9)
где у – выходная координата, а у 0 – входное воздействие.
В форме (8), (9) могут задаваться, например, уравнения движения оптимальной по быстродействию системы автоматического регулирования, если она синтезирована на ступенчатое входное воздействие. Представим уравнение (8) в виде системы дифференциальных уравнений первого порядка. Тогда система (8), (9) примет вид:
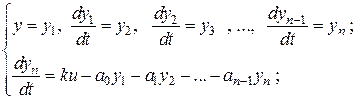(11)
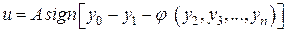. (12)
Воспользуемся вторым способом получения условий существования скользящего режима. Очевидно, в системе (8), (9) существует скользящий режим, если в каждой точке поверхности
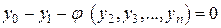
(или в некоторой области этой поверхности) выполняются неравенства:
Выполним дифференцирование по t, получим:
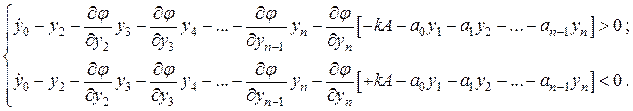
(13)
Неравенства (13) задают достаточные условия существования скользящего режима. Если в (13) перейти к нестрогим неравенствам, то получим необходимые условия существования скользящего режима. Ясно, что движение в скользящем режиме описывается уравнением:
. (14)
Предположим, что имеет место движение в скользящем режиме. Выразим 
из (14) и подставим в (13). Тогда условия существования скользящего режима можно записать в виде:
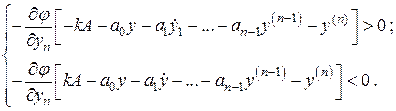(15)
Отметим, что неравенства (15) проверяются на траекториях, которые являются решением уравнения (14). Условия (15), как легко видеть, эквивалентны следующим неравенствам:
(16)
Первое из неравенств (16) представляет собой ограничение на выходной сигнал у (t). Интересно отметить, что это ограничение совпадает с динамическими возможностями объекта (8).
Далее из (14) следует, что, как и в случае автономной системы второго порядка, движение в скользящем режиме не зависит от параметров объекта (8). Однако это свойство справедливо, когда в закон управления (9) входят только частные производные, получаемые путем дифференцирования выходного сигнала. Если же закон управления формируется на основе "естественных" координат системы (ток, давление и т.п.), то через естественные координаты параметры системы входят в уравнение, описывающее движение в скользящем режиме.
Оптимальная по быстродействию система автоматического регулирования.
В оптимальной по быстродействию системе регулирования, строго говоря, скользящий режим движения в том виде, как он определялся выше, отсутствует. Действительно, хотя в оптимальной системе и имеет место движение фазовой точки по поверхности переключения, однако это движение не сопровождается бесконечной частотой переключения релейного элемента. В оптимальной системе мы имеем предельный случай скользящего режима, когда поверхность переключения образована совокупностью траекторий системы при 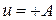, . Общие неточности в задании параметров системы, неточности в аппроксимации поверхности переключения часто приводят к тому, что в оптимальной системе имеет место типичный скользящий режим движения по поверхности переключения. Кроме того, в оптимальной по быстродействию системе автоматического регулирования режим слежения за входным воздействием всегда является скользящим.
Для линейного объекта (8) оптимальный по быстродействию закон управления традиционно формируется в пространстве ошибок и имеет вид:
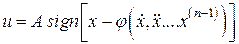, (17)
где 
- ошибка.
Следовательно, для оптимальной по быстродействию системы автоматического регулирования скользящий режим движения описывается соотношением:
. (18)
Так как
,
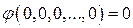то уравнение (18) имеет решение:
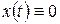, (19)
т.е. оптимальная система идеально воспроизводит любой входной сигнал, если, конечно, существует скользящий режим движения.
Выпишем применительно к системе (8), (17) условия существования скользящего режима в форме (16).Эти условия принимают вид:
(20)
Как показывают численные расчеты оптимальных систем, второе условие (20) в окрестности решения 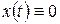всегда выполняется. Первое условие (20), принимая во внимание (19), можно переписать в виде:
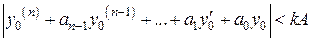. (21)
Таким образом, оптимальная по быстродействию система автоматического регулирования идеально воспроизводит любое входное воздействие y 0(t), которое удовлетворяет неравенству (21). Но, с другой стороны, неравенство (21) выделяет класс допустимых входных воздействий, которые принципиально могут быть воспроизведены объектом (8), если на управляющий параметр u наложено ограничение:
| u | 
.
Выписывая закон управления (17), мы умышленно не оговаривали класс входных воздействий, на который системы рассчитывалась как оптимальная. От этого класса зависит лишь, при каких входных сигналах в системе имеют место оптимальные переходные процессы. Что же касается режима слежения, то независимо от расчетного класса входных сигналов в системе имеет место идеальное слежение, если только оптимальный регулятор реализуется в соответствии с законом (17), т.е. в системе используются производные входного сигнала до (n -1)-го порядка включительно.
Если же, например, система рассчитывалась как оптимальная на ступенчатые входные сигналы, и оптимальный регулятор, учитывая, что производные входного сигнала равны нулю, реализовывался в соответствии с равенством:
, (22)
то режим слежения в такой системе не может быть идеальным, т.к. соотношение
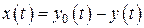
при 
не может быть решением уравнения:
. (23)
Точность слежения в этом случае можно оценивать с помощью уравнения (23).
Задача исследования.
Задачей исследования является теоретическое и экспериментальное изучение режима слежения в оптимальной системе, выявление условий существования скользящего режима и его свойств.
Объект исследования.
В качестве объекта исследования рассматривается оптимальная по быстродействию система второго порядка, изучавшаяся в лабораторной работе №1. Движение такой системы описывается уравнениями:
(24)
где ; А = 20; k = 1 или k = 5.
Функция 
задает линию переключения на фазовой плоскости 
и была рассчитана в лабораторной работе № 1
Порядок выполнения работы:
1. Уяснить сущность скользящего режима и разобраться с условиями его возникновения.
2. Экспериментально, путем цифрового моделирования в среде SIMULINK, убедиться, что при возникновении скользящего режима фазовая точка системы движется по линии переключения. Для этого необходимо провести моделирование системы для двух различных значений k в (24) и снять соответствующие фазовые траектории системы, начальные точки которых совпадают и принадлежат линии переключения. Входной сигнал у 0, как и в лабораторной работе № 1, является линейным.
Зависит ли время движения фазовой точки 
до начала координат от коэффициента k? Почему?
3. Проверить с помощью цифрового моделирования, что движение в скользящем режиме инвариантно к изменению параметров объекта (экспериментально убедиться, что в скользящем режиме движения амплитудная и фазовая частотные характеристики системы не зависят от значения коэффициента усиления k). Входной сигнал у 0 - синусоидальный: 
.
4. Предполагая входные воздействия гармоническими 
, теоретически построить в координатах 
область допустимых входных сигналов, т.е. область входных сигналов, которые принципиально могут быть воспроизведены системой (24) (при k = 1).
5. Построить экспериментально в координатах область входных сигналов, которые идеально воспроизводятся системой (24). Для этого, задавшись некоторой амплитудой В, частоту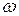 
следует плавно изменять до тех пор, пока не произойдет срыв идеального слежения. Исследовав несколько таких амплитуд, можно построить указанную область.
6. Сравнить области, полученные в п.4 и 5.
Отчет по лабораторной работе должен содержать:
1. Краткое описание условий возникновения скользящего режима.
2. Уравнение введенной вами линии переключения для системы (24) и теоретическое доказательство, что на ней существует скользящий режим.
3. Фазовые траектории системы (24) при отработке линейного входного сигнала для двух различных значений коэффициента k (при одних начальных условиях), а также теоретический расчет и результат экспериментальной проверки времени переходного процесса в системе.
4. Теоретический расчет границы области допустимых входных воздействий и ее график, а так же "экспериментальный" график границы области идеально воспроизводимых входных воздействий (оба графика изобразить на одном рисунке).
Контрольные вопросы.
1. Что такое скользящий режим движения?
2. Установить, возможно ли движение в скользящем режиме в системе:
?
3. Какой входной сигнал называется допустимым?
4. Почему при выборе В и 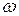из зоны срыва скользящего режима, срыв происходит не сразу после начала отработки синусоиды?
5. Как следует реализовывать оптимальную по быстродействию систему, чтобы она обеспечивала идеальное слежение за любыми допустимыми входными сигналами?
6. Какой входной сигнал называется допустимым?
Библиографический список.
1. Уткин В.И. Скользящие режимы в задачах оптимизации и управления. – М.: Наука, 1981. - 368 с.
2. Фалдин Н.В. Синтез оптимальных по быстродействию замкнутых систем управления. – Тула, ТПИ, - 1990, 100 с.
ЛАБОРАТОРНАЯ РАБОТА № 3
ПРИБЛИЖЕННЫЙ УЧЕТ В ОПТИМАЛЬНОМ
ПО БЫСТРОДЕЙСТВИЮ БАЗОВОМ ЗАКОНЕ УПРАВЛЕНИЯ
МАЛЫХ ПОСТОЯННЫХ ВРЕМЕНИ
Цель работы: изучение способа приближенного учета в оптимальном по быстродействию базовом законе управления малых постоянных времени с помощью эквивалентного запаздывания.
Теоретические сведения.
Известно, что при синтезе оптимального по быстродействию управления объём вычислений с увеличением порядка системы катастрофически возрастает. И дело здесь, собственно, не столько в численном определении самой поверхности переключения (хотя и это сопряжено с некоторыми трудностями), сколько в обработке огромного массива чисел, дискретно задающих поверхность переключения, а также в получении подходящей аппроксимации. Для систем низкого (второго и третьего) порядков вычисление поверхности переключения и её аппроксимации обычно не составляет большого труда. В соответствии со сказанным выше для систем высокого порядка большое значение приобретают приближённые способы, приёмы и методы синтеза оптимального управления.
В настоящей лабораторной работе необходимо изучить способ синтеза оптимального по быстродействию управления, позволяющий при синтезе оптимального управления приближённо учесть влияние малых постоянных времени. От других известных в литературе методов данный выгодно отличается тем, что благодаря аппроксимации системы высокого порядка системой низкого порядка с запаздыванием он достаточно точно учитывает “вклад” малых постоянных времени в оптимальный закон управления.
В передаточных функциях технических систем можно выделить большие и малые постоянные времени. Звенья, содержащие большие постоянные времени, обычно описывают силовую часть системы, а звенья, содержащие малые постоянные времени, - управляющую часть. Будем исходить из следующего: малые постоянные времени приводят к малым изменениям в поверхности переключения.
Передаточную функцию системы, полученную из исходной путём исключения звеньев, содержащих малые постоянные времени, назовём базовой, а соответствующий ей оптимальный по быстродействию закон управления - базовым законом. Совокупность звеньев, не входящих в базовую передаточную функцию, образует систему, которую будем называть дополнительной. Способы получения базового закона управления рассмотрены выше. Остановимся на тех изменениях, которые следует внести в базовый закон управления (способы получения базового закона управления рассмотрены на лекционных занятиях), чтобы учесть влияние малых постоянных времени.
Изложение указанного подхода целесообразно начать с рассмотрения конкретного примера. При этом в целях упрощения будем предполагать, что ограничение накладывается только на управление.
На рис. 1 изображена структурная схема объекта, причём пунктиром выделена базовая передаточная функция. Пусть на управляющий параметр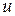 
наложено ограничение
.
Рис. 1. Cтруктурная схема объекта
Исключив звено с малой постоянной времени, легко определить оптимальный по быстродействию закон управления. Он задаётся равенством
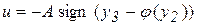, (1)
где 
- уравнение линии переключения.
Оптимальное по быстродействию управление релейно как в базовой, так и в исходной системах. Однако в исходной системе на вход базовой передаточной функции поступает координата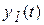 
, которая “сглаживает” релейный сигнал 
(рис. 2).
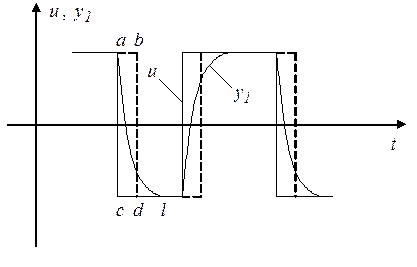
Рис. 2.
Так как 
, то базовая система обладает существенно большей “инерционностью”, чем дополнительное звено, т.е. базовая система практически не реагирует на форму быстрых изменений координаты 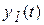, а “отслеживает” их среднее значение. Это позволяет приближённо учесть влияние дополнительного звена, заменив его звеном запаздывания. На рис. 2 пунктиром изображены запаздывающие моменты переключения, компенсирующие влияние малой постоянно времени. Следует отметить, что введение запаздывания является распространённым приёмом, который используется при аппроксимации систем высокого порядка моделями низкого порядка.
Воспользуемся известным способом синтеза систем с запаздыванием, который заключается в том, что в законе управления (1) текущие координаты 
и 
заменяются упреждёнными на запаздывание 
. Однако вместо традиционной для таких задач схемы упреждения, основанной на использовании формулы Коши решения системы линейных дифференциальных уравнений, будем использовать ряд Тейлора (траектория релейной системы не является аналитической функцией, и, строго говоря, она не может быть представлена рядом Тейлора; однако ниже будут использоваться только такие производные, которые для данной системы существуют и непрерывны). Ограничиваясь первым членом ряда Тейлора, можно записать
,
.
Из передаточной функции системы следует, что
, 
.
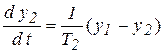Заменяя в законе (1) текущие координаты на упреждённые, получим
. (2)
Отметим, что в закон управления (2) входят все фазовые координаты объекта. Из приведённых выше рассуждений следует, что при правильно подобранном значении запаздывания закон управления (2) достаточно точно учитывает влияние малой постоянной времени 
, т.е. его можно рассматривать в качестве приближённого оптимального закона управления объектом, изображённом на рис. 1.
Остановимся на способе определения запаздывания . Известно, что для рассматриваемого объекта поверхность переключения представляет собой совокупность идущих в начало координат оптимальных траекторий, на которых допускается одно переключение управления. С другой стороны, в релейной системе (необязательно оптимальной) движение по поверхности переключения возможно в скользящем режиме. Так как оптимальная поверхность переключения состоит из траекторий движения, то её можно рассматривать как предельную поверхность скольжения. Значение запаздывания будем выбирать так, чтобы поверхность переключения, реализующая закон управления (2), также была предельной (в рамках заданной структуры) поверхностью скольжения. Это является косвенным критерием близости поверхности переключения, входящей в закон (2), к строго оптимальной поверхности. При таком выборе траектории, порождаемые законом (2), имеют характер строго оптимальных: фазовая точка объекта сначала выводится на поверхность переключения, а затем по поверхности переключения переводится в начало координат.
В соответствии с работой [1] на поверхности переключения
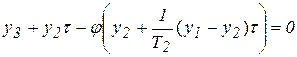(3)
условия существования скользящего режима задаются неравенствами
,
.
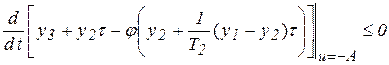Выполнив дифференцирование, получим соотношения
■ 
,
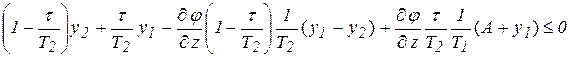,□ (4)
где
. (5)
Отметим, что неравенства (4) должны выполняться в каждой точке поверхности (3).
Так как запаздывание входит в условия существования скользящего режима (4), то для определения предельной поверхности скольжения необходимо найти такое запаздывание 
, любое малое изменение которого приводит к срыву скользящего режима движения.
Обозначим левую часть соотношений (4) 
(для статического объекта координата также входит в условия существования скользящего режима; при определении функции её необходимо выразить из уравнения (3) через 
и ). Из передаточной функции объекта следует, что фазовые переменные и изменяются в пределах
, 
. (6)
Область, выделяемую неравенствами (6), обозначим 
. Пусть
,
.
Нетрудно видеть, что
.
Величина запаздывания , при которой поверхность (3) является предельной поверхностью скольжения, удовлетворяет уравнению
.
На рис. 3 изображён график функции 
при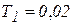 
, 
, 
. Так как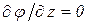 
в точке 
, то при неравенства (4) не зависят от знака управления. Для соответствующих , , как непосредственно следует из (4) и (5), левые части соотношений (4) при любом равны нулю. Этим и объясняется наличие на графике функции участка, лежащего на
оси .
Рис. 3.
Другой способ определения запаздывания основывается на приравнивании площадей криволинейного треугольника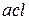 
и прямоугольника 
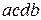(см. рис. 2). Легко убедиться, что запаздывание , если его определять указанным способом, равно . Более того, если дополнительная система состоит из 
апериодических звеньев, включённых последовательно и имеющих постоянные времени , 
, 
, 
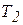, то запаздывание 
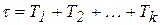. Отметим, что для рассматриваемого объекта оба способа дают примерно одинаковый результат.
На рис. 4 изображена осциллограмма отработки системой (с законом управления (2) начального рассогласования по координате . Из рисунка видно, что координата 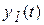имеет два излома, что соответствует двум переключениям управления. Длительность переходного процесса при этом практически не отличается от строго оптимальной. Исследование на ЭЦВМ закона управления (2) при различных значениях постоянных времени и 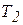показывает, что указанный подход можно успешно использовать при разносе постоянных времени в пять и более раз.
 |
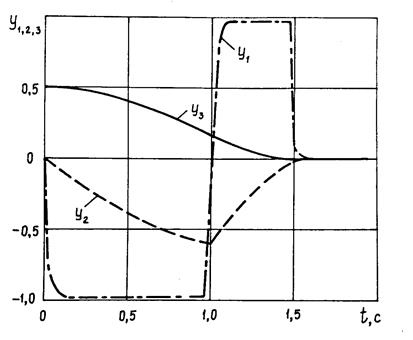Рис. 4.
Изложенный на конкретном примере способ учёта при синтезе оптимального управления малых постоянных времени практически без изменений переносится на случай любой базовой передаточной функции, а также на случай любого порядка вспомогательной системы. При этом, упреждая координаты объекта, можно использовать такое число членов ряда Тейлора, которое соответствует порядку вспомогательной системы. Это позволяет включить в закон управления все фазовые координаты объекта. Если при формировании упреждения используются членов ряда Тейлора, то такое упреждение будем называть упреждением -го порядка.
На рис. 5 изображена структурная схема объекта, у которого базовая передаточная функция остаётся прежней, т.е. 
, 
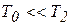. Воспользовавшись для упреждения координат двумя членами ряда Тейлора, по аналогии с действиями, проведёнными выше, получим закон управления
(7)
Запаздывание определим рассмотренными выше способами. Необходимо только иметь в виду, что не всегда выбором можно обеспечить существование скользящего режима на всей поверхности переключения. На практике существование скользящего режима на всей поверхности переключения, вообще говоря, не требуется.
Если дополнительная система состоит из апериодических звеньев, как на рис. 5, то вместо упреждения -го порядка можно использовать упреждений первого порядка. Сначала учитывается только одно апериодическое звено. С помощью упреждения первого порядка для такой системы строится оптимальный закон управления. Этот закон затем рассматривается как базовый для новой системы, в которую включается другое апериодическое звено, и т.д.
Рис. 5.
На рис. 6 изображена осциллограмма отработки системой четвёртого порядка (
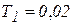, ) начального рассогласования.
 |
Рис. 6.
Оптимальный закон управления строился путём двукратного применения упреждения первого порядка. Следует отметить, что получаемый таким образом закон управления оказывается более близким к оптимальному, чем закон управления (7).
На рис. 7 изображена осциллограмма отработки начального рассогласования оптимальной системой, базовая передаточная функция которой совпадает с рассмотренной выше, а вспомогательная представляет собой колебательное звено с параметрами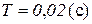 
, 
. При построении оптимального закона управления было использовано упреждение второго порядка.
Рис. 7.
Если передаточная функция объекта содержит колебательное или консервативное звено, то, как известно, оптимальные траектории образуют только часть поверхности переключения. В этом случае при выборе времени запаздывания по первому способу необходимо ориентироваться именно на эту часть поверхности.
Описанный выше приём приближённого учёта малых постоянных времени может эффективно использоваться и в более сложных задачах оптимального управления, например, если требуется построить оптимальный закон управления при наличии ограничений на фазовый вектор системы или при синтезе оптимального управления для объекта с ограничителями и т. п. Необходимо, однако, иметь в виду, что в задачах с ограничениями на фазовый вектор системы указанный приём приводит к небольшому смещению граничного участка оптимальной траектории. Это может вызвать, в конечном счете, нарушение (правда, незначительное) заданных ограничений. С практической точки зрения такие нарушения вполне допустимы.
Задачи лабораторной работы.
· теоретическое изучение способа приближенного учета в базовом законе управления малых постоянных времени с помощью эквивалентного запаздывания;
· экспериментальное исследование оптимальной по быстродействию системы управления без учета и с учетом малых постоянных времени
Объект исследования.
В качестве объекта исследования рассматривается электропривод постоянного тока, структурная схема которого приведена на рис. 8.
Рис. 8.