ОТЧЕТ
к лабораторной работе №3
по дисциплине “Математические основы системного анализа”
АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Выполнила:
студент гр. ИСТ-313
Кутушев Ш.Х.
Проверил преподаватель:
Гвоздев В.Е.
Уфа 2010
Цель работы
Целью работы является изучение методов статистического моделирования временных рядов.
Задание на работу
а) по данным, приведенным в файле «Варианты заданий» (таблица №1) оценить имеет ли место тенденция в значениях временного ряда.
б) из анализа конечных разностей определить предпочтительней порядок полинома.
3. Ход работы:
Вариант 6
Проверка гипотезы о существовании тенденции
3.1.1 Проверка средних уровней ряда
Таблица 1
| Значение параметра состояния | Значение параметра состояния |
| -3,3 | 306,5 |
| 13,8 | 328,2 |
| 34,1 | 346,3 |
| 58,0 | 371,8 |
| 77,5 | 396,7 |
| 99,0 | 415,4 |
| 118,0 | 438,5 |
| 136,8 | 457,4 |
| 162,7 | 476,4 |
| 179,0 | 497,0 |
| 202,7 | 516,9 |
| 222,3 | 538,5 |
| 245,8 | 562,6 |
| 264,7 | 582,6 |
| 289,5 | 603,7 |
По данным таблицы 1 находим среднее для двух самостоятельных выборочных совокупностей, имеющих нормальное распределение:
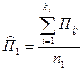= 140,0
= 455,9
Среднее, вычисленное для каждой совокупности, существенно различается между собой. Отсюда следует, что временной ряд имеет тенденцию.
3.1.2 Проверка гипотезы о равенстве дисперсий
По данным таблицы 1 произвели расчеты средних 
и эмпирического среднеквадратического отклонения S2j :
= 140,0; 
= 455,9
; 
8736,89
8935,59
где j – номер части временного ряда;
Пij – i-е значение временного ряда в j-й части;
nj -число членов в j-й части временного ряда.
Число степеней свободы эмпирических оценок среднеквадратического отклонения mk (k=1,2) определяется по правилу:
mk =nk-1
|
|
Находим значение 
:
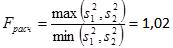
При уровне значимости 
=0,05 находим табличные значения Fкр(α, m1, m2) из приложения 1:
Fкр =2,53
Неравенство Fрасч < Fкр соблюдается, следовательно можно предположить, что с течением времени степень влияния различных факторов, определяющих значения параметра П 
не изменилась и гипотеза о равенстве дисперсий верна.
3.1.3 Проверка гипотезы о равенстве средних частей исходного ряда
Этот метод основан на проверке выполнения неравенства:
< 
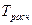Значения эмпирических дисперсий:
8736,89; 8935,59.
При уровне значимости =0,05 значения:
, 
Значения средних отклонений: 
= 140,0; = 455,9.
Рассчитаем значение величины :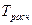
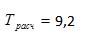
При уровне значимости =0,05 значения:
(α; m1+m2)= 2,05
Следовательно >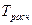
Неравенство не соблюдается, значит, гипотеза о наличии тенденций согласуется фактическим данным.
Определим характер тренда: < . Значит тренд возрастающий.
3.1.4 Метод анализа наличия тенденций, предложенный Ф. Фостером и А. Стюартом
Этот метод основан на том, что по данным исследуемого ряда определяются величины Ut и lt путем последовательного сравнения уровней ряда. Если какой-либо уровень ряда превышает по своей величине каждый из предыдущих уровней, то величине Ut присваивается значение 1, в остальных случаях она равна 0.
 |
Таким образом,
 |
И наоборот, если уровень ряда меньше всех предыдущих, то величина lt равна 1, в остальных случаях она равна 0, т.е.
Таблица 2
| Значения параметра состояния. | 
| 
|
| -3,3 | - | - |
| 13,8 | ||
| 34,1 | ||
| 58,0 | ||
| 77,5 | ||
| 99,0 | ||
| 118,0 | ||
| 136,8 | ||
| 162,7 | ||
| 179,0 | ||
| 202,7 | ||
| 222,3 | ||
| 245,8 | ||
| 264,7 | ||
| 289,5 | ||
| 306,5 | ||
| 328,2 | ||
| 346,3 | ||
| 371,8 | ||
| 396,7 | ||
| 415,4 | ||
| 438,5 | ||
| 457,4 | ||
| 476,4 | ||
| 497,0 | ||
| 516,9 | ||
| 538,5 | ||
| 562,6 | ||
| 582,6 | ||
| 603,7 |
|
|
Находим значения величин S и d:
S=∑St =29
d=∑dt = 29
Из приложения 3 находим значения μ – математического ожидания, σ1 - средне квадратической ошибки S, σ2 - средне квадратической ошибки d, которые равны:
μ=5,99
σ1=1,882
σ2=2,417
 |
 |
tкр(0.05,28)=2,05
> tкр(0.05,28), значит гипотеза о наличие тенденции в средней соответствует фактическим данным (тенденция есть), т.е. нет основания отвергать гипотезу об отсутствии тенденции в средней. 
> tкр(0.05,28),, т.е. гипотеза о наличии тенденции дисперсии не противоречит фактическим данным.