4.1 Моделирование тенденции временного ряда.
Таблица 3
| Значение параметра состояния |
|
|
|
|
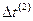
| -3,3 | - | - | - | - |
| 13,8 | 17,1 | - | ||
| 34,1 | 20,3 | 3,2 | ||
| 58,0 | 23,9 | 3,6 | ||
| 77,5 | 19,5 | -4,4 | ||
| 99,0 | 21,5 | 2,0 | ||
| 118,0 | 19,0 | -2,5 | ||
| 136,8 | 18,8 | -0,2 | ||
| 162,7 | 25,9 | 7,1 | ||
| 179,0 | 16,3 | -9,6 | ||
| 202,7 | 23,7 | 7,4 | ||
| 222,3 | 19,6 | -4,1 | ||
| 245,8 | 23,5 | 3,9 | ||
| 264,7 | 18,9 | -4,6 | ||
| 289,5 | 24,8 | 6,1 | ||
| 306,5 | 17,0 | -7,8 | ||
| 328,2 | 21,7 | 4,7 | ||
| 346,3 | 18,1 | -3,6 | ||
| 371,8 | 25,5 | 7,4 | ||
| 396,7 | 24,9 | -0,6 | ||
| 415,4 | 18,7 | -6,2 | ||
| 438,5 | 23,1 | 4,4 | ||
| 457,4 | 18,9 | -4,2 | ||
| 476,4 | 19,0 | 0,1 | ||
| 497,0 | 20,6 | 1,6 | ||
| 516,9 | 19,9 | -0,7 | ||
| 538,5 | 21,6 | 1,7 | ||
| 562,6 | 24,1 | 2,5 | ||
| 582,6 | 20,0 | -4,1 | ||
| 603,7 | 21,1 | 1,1 |
Проверяем наличие тенденции среднего уровня параметра состояния. Учитывая, что d=29-0=29 и σ1=1,882:
;
tкр(0.05,28)=2,05
Так как 
> tкр(0.05,28), то делается заключение о том, что гипотеза об отсутствии тенденции в исследуемом ряду соответствует фактическим данным.
По данным таблицы 3 провели расчеты 
, 
, 
, 
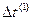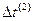. Результаты показали, что первые разности практически можно считать равными, а средняя арифметическая вторых разностей мала, ею можно пренебречь. Следовательно, тенденция изучаемого ряда может быть описана полиномом первой степени, т. е.
 |
4. Вывод:
В ходе лабораторной работы были изучены разные методы проверки наличия тенденции и дана положительная оценка по данным временного ряда о наличии тенденции. Также из анализа конечных разностей определен предпочтительней порядок полинома.
Ответы на контрольные вопросы
1. Дайте определение понятиям «тенденция, тренд»
Под тенденцией понимают некоторое общее направление развития, долговременную эволюцию. Тенденцию ряда динамики представляют в виде гладкой кривой (траектории), которая аналитически выражается некоторой функцией времени, называемой трендом.
Тренд характеризует основную закономерность движения во времени, свободную в основном от случайных воздействий.
2. Почему нельзя свести анализ тенденции к построению простой графической модели по исходным данным?
Исходные данные - это ограниченный дискретный набор значений.
Графическая модель даёт общую характеристику объекта.
Математическая модель в отличие от неё показывает поведение объекта в какой-то промежуток времени. Для использования математической модели необходимо убедиться, что данные однородны, нужно рассчитать среднее значение и убедиться, что разница не обусловлена лишь погрешностью и существует тенденция.
3. В чем содержательный смысл анализа однородности дисперсий частей временного ряда?
Однородность дисперсий свидетельствует о том, что степень влияния различных факторов, определяющих значения параметров состояния, за исследуемый период времени остается неизменной.
4. Чем обусловлена необходимость сопоставления оценок средних, вычисленных по частям временного ряда?
Она обусловлена необходимостью обнаружения тенденции и характера тренда.
5. Чем обусловлена необходимость использования разных походов для моделирования трендов?
Требованием к наибольшей точности построенной модели.