Частотная и фазовая модуляция (ЧМ и ФМ)

ЗАДАЧА 1

Стационарный случайный процесс x(t) имеет одномерную функцию плотности (ФПВ) мгновенных значений w(x), график и параметры которой приведены в таблице 1.

Требуется:

1. Определить параметр h ФПВ.
2. Построить ФПВ w(x) и функцию вероятностей (ФРВ) F(x) случайного процесса.
3. Определить первый m₁ (математическое ожидание) и второй m₂ начальные моменты, а также дисперсию D(x) случайного процесса.

Дано: a = 1; b = 6; c = 2; d = 4; e = 0,2.

 

Вид заданной функции плотности вероятности (ФПВ):

 

 

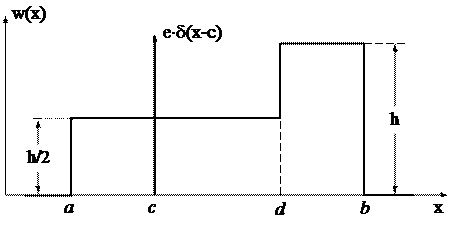РЕШЕНИЕ

1. Аналитическая запись приведенной ФПВ имеет вид:

(1)

Параметр h для ФПВ найдем из условия нормировки: 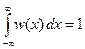(2)

Подставляем (1) в (2), получаем:

(3)

Отсюда находим параметр h:

(4)

2. Функция распределения вероятностей (ФРВ) связана с ФПВ следующим соотношением:

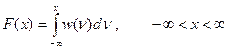(5)

По формулам (1) и (5) проводим вычисление функций w(x) и F(x) для отдельных участков.

Для x £ a = 1:

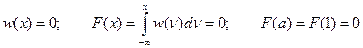(6)

Для a < x £ d ® 1 < x £ 4: 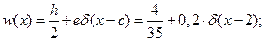(7)

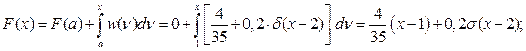(8)

Где s(x) - функция единичного скачка, равная интегралу от d - функции:

(9)

С помощью (8) находим в граничных точках:

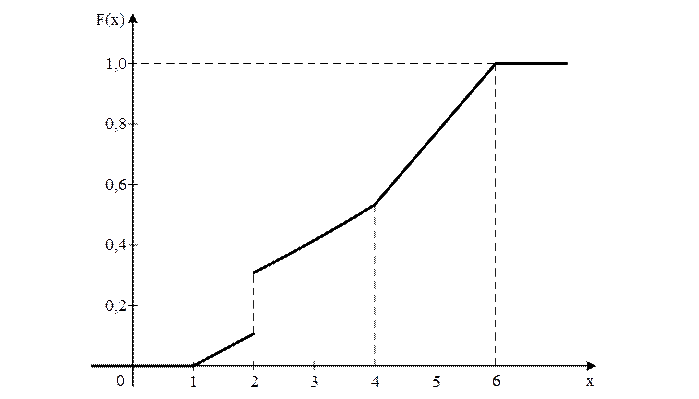
F(c – 0) = F(2 – 0) = 4/35

F(c + 0) = F(2 + 0) = 11/35

F(d) = F(4) = 19/35

Для d < x £ b ® 4 < x £ 6: 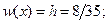(10)

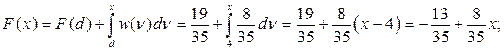(11)

Находим в граничной точке: F(b) = F(6) = 1

Для x > b = 6: 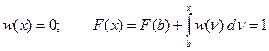(12)

 

Строим графики ФПВ и ФРВ:

 

 

 

3. Вычисляем первый начальный момент случайного процесса:

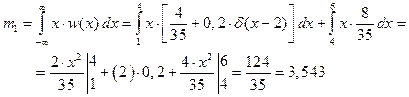(13)

Вычисляем второй начальный момент случайного процесса:

(14)

По формуле для дисперсии случайного процесса вычисляем:

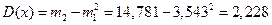(15)

 

 

ЗАДАЧА 2

Энергетический спектр гауссовского стационарного случайного процесса x(t) равен G(w). Среднее значение случайного процесса равно m_x = m₁ = M(x(t)).

Требуется:

1. Определить корреляционную функцию B(t) случайного процесса.

2. Рассчитать величины эффективной ширины спектра и интервала корреляции рассматриваемого процесса.

3. Изобразить графики G(w) и B(t) с указанием масштаба по осям и покажите на них эффективную ширину спектра и интервал корреляции.

4. Запишите выражение для функции плотности вероятности w(x) гауссовского стационарного случайного процесса и постройте ее график.

5. Определите вероятность того, что мгновенные значения случайного процесса будут меньше a – p(x < a); будут больше b – p(x > b); будут находиться внутри интервала [c,d] – p(c < x < d).

Исходные данные к задаче представлены в таблицах 2 и 3.

Дано: 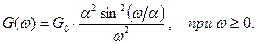G₀ = 60 В²×с/рад;

a = 350 рад/с; m_x = -4; a = -7; b = -1; c = -5,5; d = -2.

 

РЕШЕНИЕ

1. Корреляционную функцию B(t) можно определить с помощью формулы Винера - Хинчина по энергетическому спектру G(w) случайного процесса:

(1)

Для заданной функции G(w) вычисляем с помощью таблиц интегралов:

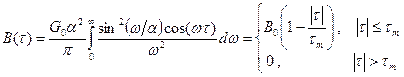(2)

где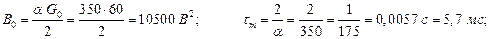

При вычислении этого интеграла был использован следующий известный интеграл [4]:

(3)

2. Определяем эффективную ширину спектра случайного процесса:

(4)

Откуда также получаем для угловой частоты:

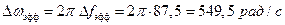(5)

Находим интервал корреляции рассматриваемого процесса:

(6)

3. Вычисляем значения функции G(w), составляем соответствующую таблицу и строим графики функций G(w) и B(t):

 

 

 

t0

 

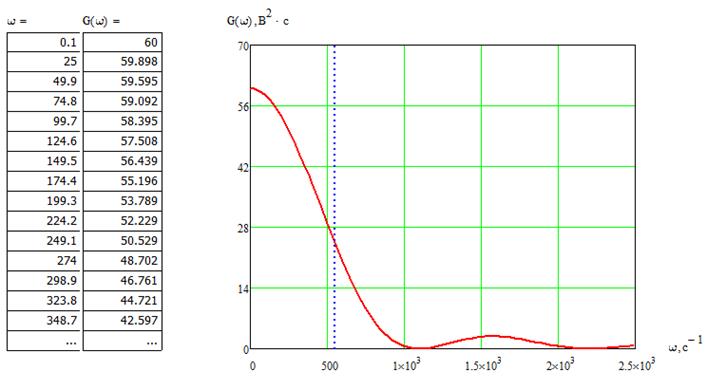
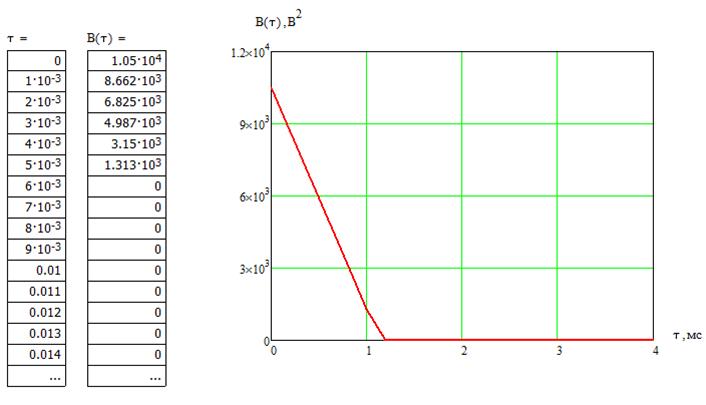
4. Вычисляем дисперсию D случайного процесса: 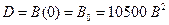(7)

Записываем выражение для функции плотности вероятности w(x) заданного нормального (гауссовского) случайного процесса:

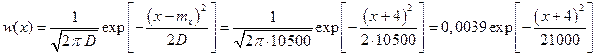(8)

Проводим вычисления для функции плотности вероятности w(x), получаем расчетную таблицу и строим график этой функции:

 

5. Для нормального случайного процесса интервальная вероятность может быть вычислена по формуле:

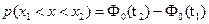(9)

где

Среднее квадратическое отклонение равно: (10)

Функция ошибок Ф₀(t) - табулирована и имеет вид:

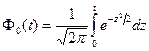(11)

По формуле (9) находим:

Вычисляем: ;

Ф₀(-¥) = -Ф₀(¥) = -0,5; Ф₀(t₂) = Ф₀(-0,0293) = -Ф₀(0,0293) = -0,01195;

Получаем: p(x < a) = -0,01195 + 0,5 = 0,48805

Аналогично, находим:

Вычисляем: ;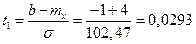

Ф₀(¥) = 0,5; Ф₀(t₁) = Ф₀(0,0293) = 0,01195;

Получаем: p(x > b) = 0,5 - 0,01195 = 0,48805

Аналогично, находим: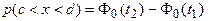

Вычисляем:

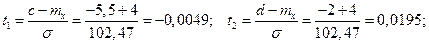
Ф₀(t₁) = Ф₀(-0,0049) = -Ф₀(0,0049) = -0,00399; Ф₀(t₂) = Ф₀(0,0195) = 0,00798;

Получаем: p(c < x < d) = 0,00798 + 0,00399 = 0,01197

 

ЗАДАЧА 3

 

Дано: Вольт-амперная характеристика (ВАХ) биполярного транзистора амплитудного модулятора аппроксимирована выражением:

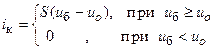
где i_к - ток коллектора транзистора,

S = 120 мА/В - крутизна характеристики,

u_б - напряжение на базе транзистора,

u_о = 0,7 В - напряжение отсечки,

u_m = 0,55 В - амплитуда входного высокочастотного сигнала.

 

Требуется:

1. Объяснить назначение модуляции несущей и описать различные виды модуляции.

2. Изобразить схему транзисторного амплитудного модулятора, пояснить принцип ее работы и назначение ее элементов.

3. Дать понятие статической модуляционной характеристики (СМХ). Рассчитать и построить (СМХ) при заданных S, u₀ и значении смплитуды входношо высокочастотного напряжения U_m.

4. C помощью статической модуляционной характеристики определить оптимальное смещение E₀ и допустимую величину амплитуды U_W модулирующего напряжения U_W×cosWt, соответствующие неискаженной модуляции.

5. Рассчитать коэффициент модуляции m_АМ для выбранного режима. Построить спектр и временную диаграмму АМ–сигнала.

 

РЕШЕНИЕ

1. Модуляцией называется физический процесс воздействия на несущее (высокочастотное) колебание с целью сообщения ему информации о передаваемом сообщении (“погрузке сигнала”).

Суть модуляции состоит в изменении одного из параметров несущего колебания пропорционально величине передаваемого сообщения. Особенностью модуляции является соотношение для частот:

w₀ >> W_В (1)

где w₀ - частота несущего колебания,

W_В - высшая частота для модулирующего сообщения.

 

 

ОСНОВНЫЕ ВИДЫМОДУЛЯЦИИ

 

Амплитудная модуляция (АМ)

При АМ изменяемым параметром является амплитуда высокочастотного (ВЧ) колебания. В случае АМ одним тоном с частотой W получается известное выражение:

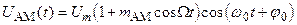(2)

где 0 £ m_АМ £ 1 - коэффициент модуляции,

j₀ - фаза несущего колебания.

 

Частотная и фазовая модуляция (ЧМ и ФМ)

При ЧМ изменяемым параметром является частота, при ФМ - фаза несущего колебания. При модуляции одним тоном частоты или фазы несущего колебания (оба эти вида модуляции в силу их малого различия именуются угловой модуляцией) имеем сигнал частотной и фазовой модуляции следующего вида:

U_ЧМ,ФМ(t) = U_mcos(w₀t + m_Ч,ФcosWt + j₀) (3)

Где использованы обозначения -

- при частотной модуляции: m_Ч = Dw/W - индекс частотной модуляции, Dw - девиация частоты.

- при фазовой модуляции: m_Ф = Dj, Dj - девиация фазы.

Если несущему колебанию придать вид последовательности импульсов (при этом их длительность значительно меньше пауз между импульсами), то появляется новый класс видов модуляции. Здесь можно модулировать временное положение импульсов, их длительность, частоту следования, амплитуду и другие параметры.

Кроме того, если в спектре АМ сигнала подавить несущую и одну из двух боковых полос сигнала, то оставшаяся боковая полоса позволяет осуществить связь по способу однополосной модуляции (ОМ). Сигнал ОМ позволяет уменьшить занимаемую полосу частот канала связи, увеличить мощность сигнала и уменьшить уровень шумов приемника.

 

2. Схема транзисторного амплитудного модулятора имеет вид:

 

 

Назначение элементов схемы:

Е_п - напряжение питания каскада модулятора,

VT - усилительный, нелинейный элемент схемы (транзистор),

U_см - напряжение смещения каскада, задающее его рабочую точку,

U_нес - напряжение несущего высокочастотного колебания,

U_мод - модулирующее низкочастотное напряжение сигнала,

Тр₁, Тр₂ - разделительные трансформаторы ВЧ и НЧ колебаний несущего и модулирующего напряжений,

С_ш - конденсатор, шунтирующий (то есть закорачивающий) трансформатор Тр₂ для токов ВЧ - несущей,

L, C - индуктивность и емкость колебательного контура, выделяющего первую гармонику коллекторного тока, то есть настроенного на ее частоту,

С_р - разделительный конденсатор, пропускающий на выход схемы выходной модулированный ВЧ сигнал U_вых и не пропускающий постоянную составляющую коллекторного напряжения транзистора,

С_п, С_см – конденсаторы фильтров цепей питания всей схемы и базовой цепи смещения, служат для уменьшения выходного сопротивления источников питания и устранения паразитного влияния индуктивности соответствующих подводящих проводов.

 

ПРИНЦИП РАБОТЫСХЕМЫ

На базу транзистора VT подается ВЧ сигнал несущей U_нес, смещенной на величину U_см + U_мод, благодаря чему транзистор VT открывается импульсами базового тока с изменяющимися углами отсечки в соответствии с напряжением смещения U_см + U_мод. В коллекторной цепи транзистора возникают импульсы тока с частотой несущей, промодулированные по амплитуде модулирующим напряжением. Колебательный контур LC выделяет из импульсов коллекторного тока первую гармонику - модулированный высокочастотный сигнал, который через разделительную емкость С_р попадает на выход каскада.

 

3. Статической модуляционной характеристикой (СМХ) называется зависимость амплитуды первой гармоники несущего колебания на выходе модулятора от напряжения смещения при постоянной амплитуде входного высокочастотного колебания.

При подаче смещения на вход схемы модулятора U_см = Е и высокочастотного колебания несущей U_нес(t) = U_mcos(w₀t), к базе транзистора будет приложено напряжение:

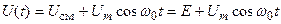(4)

Получаем условие отсечки базового тока:

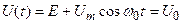(5)

Откуда находим угол отсечки:

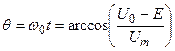(6)

По заданной ВАХ транзистора находим максимальный коллекторный ток:

(7)

Первую гармонику коллекторного (выходного) тока I₁(E) находим с помощью функции Берга:

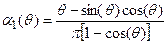(8)

Получаем: 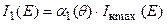(9)

 

По формулам (6¸9) задаваясь значениями Е вычисляем соответствующие значения q, a₁(q) и I₁(E).

 

Строим расчетную таблицу:

 

E, В	q(E), рад	a1(E), рад	Ik(E), мА	I1(E), мА
0,25	0,613	0,249		2,988
0,35	0,881	0,342		8,200
0,45	1,099	0,405		14,589
0,55	1,295	0,452		21,696
0,65	1,480	0,487		29,200
0,75	1,662	0,512		36,833
0,85	1,847	0,528		44,338
0,95	2,043	0,536		51,445
1,05	2,261	0,535		57,833
1,15	2,529	0,525		63,046
1,25	3,142	0,500		66,033

 

Строим СМХ, то есть зависимость первой гармоники коллекторного тока от напряжения смещения I₁ = I₁(E):

 

 

 

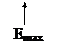
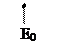
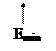
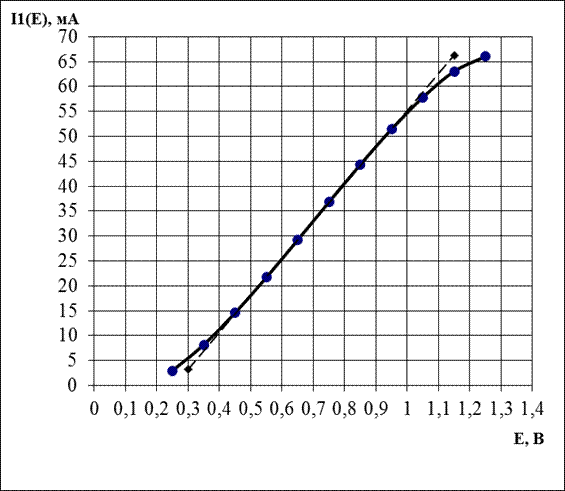
4. С помощью СМХ получаем минимальное E_min и максимальное Е_max смещение, при которых СМХ начинает отклоняться от соответствующей линейной характеристики:

E_min = 0,43 В; Е_max = 0,99 В.

Вычисляем оптимальное смещение:

Вычисляем допустимую величину амплитуды модулирующего напряжения, соответствующую неискаженной модуляции:

 

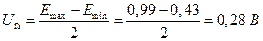
5. Используя СМХ определяем минимальное и максимальное неискаженное значение первой гармоники тока:

I_1min = I₁(E_min) = 13,242 мА; I_1max = I₁(E_max) = 54,108 мА.

Вычисляем коэффициент модуляции для выбранного режима:

Амплитуда тока несущей компоненты АМ сигнала (с частотой w₀) равна:

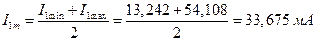
Амплитуда боковых компонент АМ сигнала с частотами w₀ ± W равна:

 

 

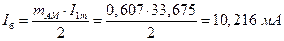
Спектральная диаграмма АМ - сигнала имеет вид:

 

 

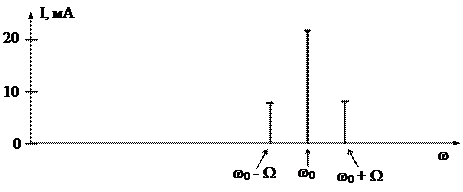Временная диаграмма АМ - сигнала имеет вид (время и частота выбраны произвольно в условных единицах):

 

 

ЗАДАЧА 4

Дано: Вольт-амперная характеристика (ВАХ) амплитудного детектора аппроксимирована выражением:

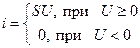
Напряжение АМ колебания на входе детектора:

U_АМ(t) = U_m [1 + m_АМ cos(2pFt)]cos(2pf₀t)

где S = 50 мА/В; m_АМ = 0,75; k_д = 0,8;

U_m = 1,7 B; f₀ = 700 кГц; F = 5,0 кГц.

 

Требуется:

1. Пояснить назначение детектирования модулированных колебаний. Изобразить схему диодного детектора и описать принцип ее работы.

2. Рассчитать необходимое значение сопротивления нагрузки детектора R_Н для получения заданного значения коэффициента передачи детектора k_Д.

3. Выбрать значение емкости нагрузки детектора C_Н при заданных f₀ и F.

4. Рассчитать и построить спектры напряжений на входе и выходе детектора. Значения S, m_AM и k_Д даны в таблице 5, а значения U_m, F и f₀ – в таблице 6.

 

РЕШЕНИЕ

1. Назначение детектирования модулированных колебаний в выделении исходного низкочастотного сигнала модуляции, пропорционального передаваемому сообщению. То есть операция детектирования сигнала противоположна модуляции.

Схема диодного детектора имеет вид:

 

 

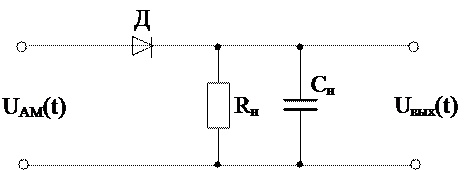При подаче на вход детектора АМ - сигнала в моменты отпирания диода Д конденсатор заряжается почти до амплитудного значения U_АМ(t), затем, при запирании диода Д конденсатор С_н медленно разряжается через резистор R_н. То есть, при медленном изменении по амплитуде напряжения U_АМ(t) на входе детектора, напряжение на конденсаторе С_н будет повторять амплитудные значения входного ВЧ - напряжения, повторяя тем самым напряжение модулирующего сигнала.

 

2. По коэффициенту передачи детектора k_д определяем соответствующий угол отсечки q:

k_д = cos(q) ® q = arccos(k_д) = arccos(0,8) = 0,644 рад.

С помощью соотношения 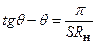вычисляем сопротивление нагрузки детектора:

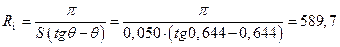Ом

Выбираем ближайший номинал резистора из стандартного ряда:

R_н = 560 Ом

 

3. Для того, чтобы нагрузочная цепь выполняла роль фильтра для высоких частот f₀ и не подавляла модулирующий сигнал частоты F необходимо выполнение условий:

Откуда получаем условие выбора С_н: С_min << C_н << C_max

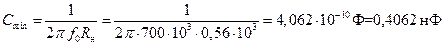
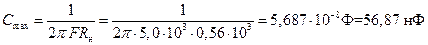
Для наилучшего выполнения обеих неравенств можно использовать среднее геометрическое C_min и C_max:

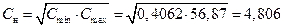нФ

Выбираем ближайший номинал конденсатора из стандартного ряда:

С_н = 4,8 нФ.

 

4. На входе детектора кроме несущей компоненты U_m с частотой f₀ будут присутствовать две боковые компоненты с частотами f₀ ± F и амплитудами:

На выходе детектора будет присутствовать спектральная компонента с частотой модуляции F и амплитудой:

U_{m вых} = m_АМ k_д U_m = 0,75×0,8×1,7 = 1,02 В

 

Спектр напряжения на входе детектора:

 

Спектр напряжения на выходе детектора:

 

 

ЛИТЕРАТУРА

 

1. Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов. – М.: Радио и связь, 1986.

2. Андреев В.С. Теория нелинейных электрических цепей. – М.: Радио и связь, 1982.

3. Баскаков С.Н. Радиотехнические цепи и сигналы: Учебник для вузов по специальности “Радиотехника”. – М.: Высшая школа, 1988.

4. Двайт Г.Б. Таблицы интегралов и другие математические формулы. – М.: Наука, 1977.