Метод наискорейшего спуска.

Согласно методу наискорейшего спуска, поиск оптимального решения начинается с допустимого решения и продолжается в направлении век­тор -градиента целевой функции до тех пор, пока не будет достигнута точка границы допустимой области. В этой точке направление поиска меняется в соответствии с определенными правилами. Исходное движение в направлении век­тор - градиента F обосновано тем, что в этом направлении увеличение F происходит в наибольшей степени.

Рассмотрим применение этого метода к задачам линейного программирования. Необходимо максимизировать целевую функцию

F(x₁, x₂,…, x_n) = c₁x₁ + c₂x₂ +…+ c_nx_n (101)

при линейных ограничениях

а₁₁х₁ + а₁₂х₂ + … + а_1nх_n = b₁,

а₂₁х₁ + а₂₂х₂ + … + а_2nх_n = b₂,

…………………………………

а_m1х₁ + а_m2х₂ + … + а_mnх_n = b_m, (102)

где с_j, а_ij, b_i – константы.

Предполагается, что в ограничениях (102) могут быть как ограни­чения- равенства, так и ограничения-неравенства со знаками ≥ или ≤. В этом случае ограничения-неравенства со знаками ≥ необходимо преобразовывают к виду неравенств со знаком ≤, умножая обе части ограничений на —1. Ограни­чения-равенства, если они есть, остаются без изменений.

Предположим, что вектор {x₀} = {x_1,0, x_2,0, …, x_n,0} является до­пустимым решением и не лежит на границе области допустимых решений. Лучшее решение { x ₁ } при F₁ > F₀ получается по формуле

{x₁} = { x₀} + λ {d₀}, (103)

где λ — длина шага, 0 ≤ λ ≤ ε.

Вектор столбец {d₀} есть вектор, транспонированный к вектору-градиенту f ( x₀ ), определяемому выражением

f ( x ) = [∂f/∂x₁, ∂f/∂x₂, …, ∂f/∂x_n] (104)

Другими словами, элементы вектор - градиента есть частные производные от целевой функции по каждой из переменных. В случае линей­ной функции

f ( x ) = [c₁, c₂, …, c_n] (105)

и {d₀} = { c₁, c₂, …, c_n} (106)

Элементы вектора {x₁} лучше всего выбрать при максимально воз­можном значении λ так, чтобы вектор {x₁} остался внутри допустимой области. Таким образом, выбранная величина ограничена двумя фак­торами.

Во-первых, с увеличением λ одна или несколько переменных x_{j ,1}могут уменьшиться до нуля. Далее, поскольку условие неотрица­тельности x_{j ,1}задано неравенством x_j,1 = x_{j ,0} + λd_{j ,0} ≥ 0, то для каждого d_{j ,0} < 0 значение λ ограничено величиной — x_{j ,0} / d_j,0. Для d_{j ,0} = 0 значение λ становится бесконечно большой величиной, тогда как для положительных d_j,0 λ становится отрицательным и потому неприемлемо. По этой причине значение λ ограничено сверху величи­ной λ₁ заданной соотношением

λ₁ = min [– x_j,0 / d_j,0], (107)

в котором рассматриваются лишь положительные x_j,0 и отрицатель­ные d _j,0. Уравнение (107) дает наибольшее значение λ, при котором ни одно из положительных x_j не превращается в отрицательное.

Во-вторых, при увеличении λ можно достигнуть одной или нес­кольких границ допустимой области. Каждое некритическое огра­ничение получается умножением 1-й строки [ a _i] матрицы A на век­тор нового решения { x _i}. Это решение допустимо, если [a_i] ( {x₀} + λ {d₀} ) ≤ b_i. Отсюда следует, что для каждого некритического ограничения значение λ ограничено величиной ( b_i – [ a_i] {x₀} ) / ([ a_i] {d₀} ) при условии, что [ a _i] { d₀ } есть положительное число.

Таким обра­зом, λ ограничено также величиной λ₂, которая задана соотношением

λ₂ = min 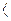(b_i – [ a_i] { x₀} ) / ([ a_i] {d₀} ) 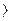, (108)

в котором рассмотрены лишь положительные [ a _i] { d₀ } и некрити­ческие неравенства.

Если λ > λ₁, то некоторые переменные станут отрицательными, а если

λ > λ₂, то перестанут выполняться некоторые ограничения. Поэтому за длину шага принимают наименьшее из двух чисел λ₁ и λ₂. В случае линейной целевой функции λ равна верхнему пределу ε.

По достижении границы значение Fможно улучшить, лишь изме­нив направление поиска. Если двигаться от точки {x_v} в направле­нии {r}, то скорость изменения F равна f(x {r}, где { r } имеет длину, равную единице, т. е. [r] {r} = 1. Так как при достижении границы одна из переменных x_jv обращается в нуль, то, для того чтобы не вый­ти из допустимой области, r_j и λ следует выбрать таким образом, чтобы новые значения x_j удовлетворяли условиям

x_j = x_jv + λ r_j ≥ 0, (109)

но поскольку x_jv = 0 и λ > 0, то отсюда следует, что r_j ≥ 0.

С другой стороны, в случае, когда при {x} = {x_v} достигается граница, определяемая i-м ограничением, то [a_i] {x_v} = b_i. Чтобы не выйти из допустимой области, {r} и λ следует выбрать так, чтобы новое значение {x} удовлетворяло условию

[a_i] {x} = [ a_i] ({ x_v} + λ {r} ) ≤ b_i (110)

Но так как [a_i] ({ x_v} = b_i,то для λ > 0 [a_i] {r} ≤ 0. В случае ограничения-равенства [a_i] {r} = 0.

Наилучшее направление, удовлетворяющее вышеприведенным ус­ловиям, есть направление, в котором максимальна скорость изменения F, т. е. его можно получить, решая следующую задачу линейного программирования, если выбрать {r} так, чтобы для переменных x_jv = 0 выполнялось условие 0 ≤ r _j ≤ 1, а для других, отличных от нуля переменных r _j0, принимало значение -1 ≤ r _j ≤ 1.

Необходимо максимизировать скорость изменения F при {x} = {x_v}

[a_i] {r} {≤, =} 0,

0 ≤ r _j ≤ 1 для x_jv = 0

-1 ≤ r _j ≤ 1 для x_jv > 0 (112)

В результате выбираем не самый лучший, но допустимый вектор {r}.
Найдя {r}, по наименьшему из λ₁ и λ₂, заданным формулами (107)
и (108), снова получаем значение λ. Когда f( x _v) { r} отрицательно,
процесс завершается, это означает, что найдено оптимальное значение­
Необходимо отметить, что в случае линейных ограничений вектор { r } выбирается таким образом, чтобы поиск продолжался вдоль гра­ницы критического ограничения.

Этот метод можно проиллюст­рировать следующей диаграммой (рис. 10). Поиск решения можно начать с допустимой точки, например a, в направлении вектор - градиента ab, ортогонального к линии постоянного значе-

ния целевой функции F ₀ в точке а. Точка b является границей допустимой области, в которой целевая функция F имеет значение F ₁большее, чем F ₀ Легко видеть, что любое движение в том же направлений от точки а неосуществимо, и потому выбираем новое направление поиска. Это направление выби­рается вдоль линии bc на одной из границ, определяе -

мой ограничениями допустимой области. Это направление снова меняется на направление cd, пока, наконец, в точке d достигается максимальное значение целевой функции.