Ограничения – неравенства.

Цели и задачи дисциплины, ее место в учебном процессе.

Цель преподавания дисциплины - научить будущего инженера-строителя методам оптимального проектирования. Оптимальный расчет необходим при решении задач организации, экономики, конструирования в строительстве.

Задача изучения дисциплины – последовательное усвоение студентами теоретических основ и выработка практических навыков к выполнению расчетов и оптимального проектирования.

Перечень дисциплин, усвоение которых студентами необходимо для изучения данной дисциплины:

- высшая математика (разделы - пределы, дифференциал и производная; функция многих переменных; частные производные, максимум и минимум функций многих переменах, теория определителей и матриц);

- спецкурс по математике - методы оптимизации;

- информатика (разделы программирования на алгоритмических языках БЕЙСИК, Паскаль и их модификаций).

Распределение по темам

 

№ Те- мы	Наименование темы
	Вводная лекция
	Тема 1. Проектное дело и проблемы оптимального проектирования
	Тема 2. Постановка некоторых основных задач оптимального проектирования строительных конструкций
	Общие сведения о решении задач оптимального проектирования строительных конструкций
	Методы решения задач оптимального проектирования
	Тема 3. Методы решения задач линейного программирования. Графические методы
	Методы решения задач линейного программирования. Симплекс-метод
	Методы решения задач линейного программирования. Метод наискорейшего спуска.
	Тема 4. Методы решения задач нелинейного программирования. Метод динамического программирования. Метод наименьших квадратов.

 

Содержание учебных занятий

 

№ темы	Лек ции Пракич. заня тия Лаб. час	Наименование темы. Наименование лекции Содержание лекции (изучаемые вопросы)
		Вводная лекция. Краткий обзор развития методов расчета строительных конструкций (СК). Понятие оптимального проектирования СК. Краткий обзор развития методов оптимального расчета СК. Общие характеристика развития методов оптимального проектирования.
		Тема 1.Проектное дело и проблемы оптимального проектирования. Пример оптимального проектирования корпуса РВС. Вариантное проектирование СК. Основы САПР. Методологические основы оптимизации. Математическая модель системы.
		Тема 2.Постановка некоторых основных задач оптимального проектирования строительных конструкций. Общая математическая формулировка и технико-экономическое содержание основных задач. Целевая функция.
	Построение целевой функции для металлических, деревянных и ж/б конструкций. Ограничения – неравенства. Уравнения состояния. Структура математического описания задачи оптимального проектирования СК.
		Тема 3.Методы решения задач линейного программирования. Общие сведения о решении задач оптимального проектирования СК. Задача оптимизации СК – задача математического программирования. Линейные задачи (линейное программирование). Особенности уравнений функции цели и ограничений – неравенств. Пример математического описания линейной задачи.
		Тема 4.Нелинейные задачи (нелинейное программирование). Особенности уравнений функции цели и ограничений – неравенств. Пример математического описания нелинейной задачи
		Методы решения задач оптимального проектирования. Методы для решения линейных задач – метод целочисленного программирования, метод наискорейшего спуска, симплекс-метод. Методы для решения нелинейных задач – градиентные способы, методы с использованием производных функций, ме-тод наискорейшего спуска.
		Методы для решения нелинейных задач – градиентные способы, методы с использованием производных функций, метод наискорейшего спуска. Методы решения задач линейного программирования графическим способом. Методика решения.
	Пример решения задачи оптимального проектирования графическим способом (задача Фурье о возможности установки пушки с обслугой на помосте)
		Методы решения задач линейного программирования симплекс-методом. Методика решения, общие положения.
	Пример решения линейной задачи симплекс – методом (оптимальное распределение ресурсов завода резервуарных конструкций).
		Методы решения задач линейного программирования. Метод наискорейшего спуска.
	Пример решения задачи оптимального проектирования методом наискорейшего спуска.
		Методы решения задач нелинейного программирования. Метод наискорейшего спуска. Метод динамического программирования.
		Пример расчета составной стальной балки минимального веса методом динамического программирования. Составление математического описания задачи оптимального проектирования.
	Метод наименьших квадратов. Пример аппроксимации экспериментальных результатов эмпирической формулы.

 

 

Вопросы для рубежного контроля

I модуль

1. Что лежит в основе принципа концентрации материала?

2. В чем основа вариантного проектирования?

3. Что такое оптимальная конструкция?

4. В чем основа постановки задачи оптимизации строительных конструкций?

5. Когда задача оптимизации сводится к определению безусловного экстремума целевой функции?

6. Когда задача оптимизации сводится к определению условного экстремума целевой функции?

7. Когда можно использовать симплекс-метод при решении задач оптимального проектирования строительных конструкций?

8. Как называются переменные целевой функции?

9. В каких задачах программирования можно использовать градиентные методы?

10. От чего зависит выбор метода решения задач оптимального проектирования?

11. В чем суть симплекс-метода?

12. Когда можно применить метод динамического программирования при решении задач оптимального проектирования?

13. Как выбираются независимые переменные в задачах оптимального проектирования строительных конструкций

14. Как устанавливаются ограничения?

15. Укажите, какие функция является функцией одной переменной?

16. Что называется оптимальным значением задачи линейного программирования?

17. Может быть оптимальное решение неединственным и, если да, то когда?

18. Когда применяют графические способы решения задач оптимального проектирования?

19. Какие методы решения задач используются в задачах линейного программирования?

20. Какие методы решения задач используются в задачах нелинейного программирования?

21. В чем суть динамического программирования?

 

Вопросы для проведения зачетов

 

Проектное дело и проблемы оптимального проектирования.

1. Когда заложены основы оптимального проектирования строительных конструкций? Приведите пример оптимального задания формы и геометрических параметров стальных резервуаров. Кто разработал условия оптимизации резервуаров?

2. Как определялась степень оптимальности строительных конструкций в 19 веке? Что дало в деле оптимизации строительных конструкции разработка типовых проектов?

3. Назовите основные положения системы САПР.

Постановка некоторых основных задач оптимального проектирования

1. Как формируется математическая модель системы?

2. Сформулируйте необходимые и достаточные условия существования оптимального решения.

3. Как определяются границы системы?

4. Что такое критерий оптимальности?

5. Как назначаются независимые переменные?

6. Покажите на примере, как осуществляется последовательность решения задач оптимизации.

7. Какие виды функций одной переменной вы знаете?

8. Покажите монотонно возрастающие и убывающие функции.

9. Что такое унимодельность функций?

10. Что такое глобальный и локальный оптимум функции?

Общие сведения о решении задач оптимального проектирования.

1. Назовите основные положения линейного программирования.

2. Когда можно использовать графические методы решения задач оптимального проектирования?

 

 

 

Учебная литература и иные информационные источники

4.1. Основная литература

1. Мажид К.И. Оптимальное проектирование конструкций. М.: Высшая школа, 1979.

2. Брусенцев А.Г. Исследование операций и методы оптимизации. Учебное пособие. Белгород – 1998 г.

3. Никитин Е.В. Оптимальное проектирование строительных конструкций. Конспект лекций. Саратов, СГТУ. 1999 г

4. Денисова А.П. Оптимальное проектирование строительных конструкций. Методические указания. Саратов, СГТУ, 2008. 30С.

5. СНиП 2.01.07-85* Нагрузки и воздействия. М.:«Стандарт», 2005.

6. СНиП II-23-81* Стальные конструкции. М., «Стандарт», 2007.

7. СНиП 52-01-2003 Бетонные и железобетонные конструкции. М.,: «Стандарт», 2004.

8. СНиП II-25-80 Деревянные конструкции. М.: «Стандарт», 2006.

 

Дополнительная литература

1. Реклейтис Г., Рейвиндрен А. Оптимизация в технике. Т.1, Т2. М., Мир, 1986 г.

3. Демьянов В.Р., Малозенов В.Н. Введение в минимакс. М., 1972 г.

4.. Химмельблау Д. Прикладное нелинейное программирование. – М.: Мир, 1976 г.

5.. Данди Г. Дж. Линейное программирование, его применение и обобщение. М.: Прогресс, 1966.

6. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. – М.: Наука, 1986.

 

 

Курс лекций

ТЕМА 1. ПРОЕКТНОЕ ДЕЛО И ПРОБЛЕМЫОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ

 

Теория оптимального проектирования строительных конструкций начала создаваться еще в 19 веке. Так В. Г. Шухов предложил оптимальную форму и геометрические параметры наземных резервуаров для хранения жидких продуктов. По его предложению квадратная форма резервуара была заменена на более оптимальную форму – цилиндрическую. Действительно, работа стенки квадратного в плане резервуара на гидростатическое давление характеризуется, как известно, возникновением значительных краевых изгибающих моментов в угловых сечениях (рис. 2, а). В то время, как стенка круглого в плане резервуара работает на растяжение, что соответствует наиболее оптимальной работе металла (рис. 2, б).

 

H

N

N

 

q=gh

R R

 

В.Г. Шухов установил оптимальные размеры вертикальных стальных резервуаров постоянного объема, при которых расход металла будет наименьшим. Резервуар со стенкой постоянной толщины имеет минимальную массу при условии, что суммарная масса днища P_дн и покрытия Р_покр вдвое больше массы стенки Р_ст:

P _min=> (P_дн + Р_покр) = 2 Р_ст (1)

Резервуар со стенкой переменной толщины имеет минимальную массу при условии, что суммарная масса днища P_дн и покрытия Р_покр равна массе стенки Р_ст:

P _min=> (P_дн + Р_покр) = Р_ст (2)

Известная конструкция деревянного кружального свода, предложенного В.Г. Шуховым, была возведена один раз, так как в то время подрядчики брали с пуда веса конструкций. Масса свода была в несколько раз меньше известных конструкций – балок, арок, ферм.

Стремление получить оптимальное решение всегда было основным стимулом при разработке многих задач проектирования, технологии, управления и др. Прежде степень оптимальности определялась сравнением разработанных вариантов, однако их возможное количество обычно бывало небольшим. Анализ нескольких вариантов приводил к ситуации, в которой можно было оценить их относительные достоинства и выбрать наилучший из них. Сколь значительно выбранный вариант лучше других вариантов решало жюри специалистов-проектировщиков. Успех этого метода, очевидно, зависит от имеющего опыта проектирования, грамотности жюри. Этот метод оправдывает себя в период постепенной эволюции конструкций, но не применим к революционным изменениям.

Положение резко изменилось после появления ЭВМ. Во-первых, стало возможно разрабатывать не два-три, а сотни и тысячи вариантов и в результате этого подходить к оптимальному решению значительно ближе и, во-вторых, что еще более существенно, появилась возможность определения теоретически оптимального решения задачи.

Свой предмет теория оптимального проектирования берет из проектного дела. Как и многие другие виды человеческой деятельности, проектирование ставит перед собой задачу, не имеющую, в принципе, строгой формулировки. Ее место занимают общие требования, которые можно свести к следующим: эффективность, надежность, долговечность, технологичность, эстетичность, экономичность.

Перечисленные требования противоречивы в том смысле, что стремление наиболее полно удовлетворить одному из них приводит к невыполнению других. Таким образом, необходим комплексный учет всех требований, и в этом основная трудность проектирования.

 

Давайте это представим на следующем примере. При проектировании цилиндрического резервуара радиусом R и высотой h толщина стенки определяется по безмоментной теории оболочек. В стенке возникают растягвающие усилия, пропорциональные гидростатическому давлению (р_х). Максимальное усилие возникает в уровне днища резервуара. Учитывая, что толщина

стенки резервуара пропорциональна усилию, то, практически, ее определение можно проводить графически в зависимости от максимальной толщины и ширины поясов (рис. 3).

На рис. 2 приведены три варианта конструирования стенки резервуара, на котором можно видеть изменение массы стенки для каждого варианта. Условно будем считать, что для изготовления стенки используются полосы постоянной толщины размерами 2πR*h, 2πR*(h/2) и 2πR*(h/4) соответственно.

Для первого варианта:

- расход стали P₁= 2πR*h*t₁ ρ; - длина кольцевых сварных швов L_ш=0.

Для второго варианта:

- расход стали P₂= 2πR*(t₁*h/2+ t₂*h/2) ρ; - длина кольцевых сварных швов L_ш=2πR.

Для третьего варианта:

- расход стали P₃= 2πR*(t₁*h/4+ t₂*h/4+ t₃*h/4+ t₄*h/4) ρ; - длина кольцевых сварных швов L_ш=6πR.

Проведем сравнение вариантов конструкций стенки резервуара по расходу стали, трудоемкости изготовления и расходу присадочного материала (сварочной проволоки). Таблица 1

Сравнение вариантов конструкции стенки

 

№ варианта	Расход стали	Расход сварочной проволоки	Трудоемкость
а)	Рmax	Smin	Tmin
b)	P< Рmax	S> Smin	T> Tmin
с)	Pmin	Smax	Tmax

 

Как видно из проведенного сравнения (табл. 1), что стенка минимальной массы имеет максимальные показатели расхода присадочного материала и трудоемкости изготовления. В этом случае задача проектирования стенки минимальной массы не является оптимальной по другим требованиям. Поэтому для оценки эффективности конструктивного решения стенки резервуара недостаточно выполнения одного из требований, предъявляемых к ней. Оптимизация стенки резервуара состоит в том, чтобы найти такую конструкцию, которая, обеспечивая достаточно высокую надежность, требовала бы минимума затрат на ее изготовление, т.е. найти компромиссное решение. Задача проектирования стенки резервуара усложняется и возникает необходимость учитывать не один параметр – массу стенки, а еще один или даже несколько параметров. То есть однопараметрическая задача оптимального проектирования превращается в многопараметрическую.

В основерешений многопараметрических задач оптимального проектирования лежит метод исследования операций. Существо операционной задачи состоит в построении математической модели той ситуации, в которой требуется принять решение. Математическая модель представляет собой, в общем случае, описание некоторой основной величины F в ее зависимости от управляемых переменных х_i и неуправляемых параметров с_j:

_k

F = Σ α_r f_r(x₁,…, x_i,…,x_n; c₁,…, c_i,…, c_m), (3)

^r=1

при этом учитываются условия – ограничения, налагаемые на переменные:

g_s(x₁,…, x_i,…,x_n; c₁,…, c_i,…, c_m) = 0; (s=1, 2,…p); (4)

y_t(x₁,…, x_i,…,x_n; c₁,…, c_i,…, c_m) ≥ 0; (t=1, 2,…q), (5)

где α_r - весовые коэффициенты или множители значимости, позволяющие объединить в один комплексный показатель Р несколько разнородных показателей f_r с учетом их размерности и приведением к одной измерительной шкале, обычно денежной.

f_r - технико-экономические показатели – вес конструкции, стоимость материалов, трудоемкость изготовления, срок изготовления или возведения и т.п.

F – критерий функционирования системы – критерий технико - экономической эффективности проектируемой конструкции;

x_i, c_i – учитываемые величины при проектировании.

Управляемые переменные x₁,…, x_i,…,x_n – это те величины и характеристики, которые в нашем случае может назначить проектировщик (материал, расчетные сопротивления, размеры поперечного сечения, толщина и т.п.). Неуправляемые параметры c₁,…, c_i,…, c_m – величины, значения которых не подлежат изменению в процессе проектирования (предельная гибкость, коэффициенты условия работы, величина усилий и т.п.).

Применение операционного метода предусматривает выявление и анализ каждой из учитываемых переменных и обоснованное отнесение этой величины к той или иной группе факторов (ранжирование переменных).

Формирование показателя F (3) и ограничений (4), (5) представляет собой достаточно сложное и подробное исследование, выполняемое специальной группой операционистов, в состав которой входят инженеры, математики, экономисты, психологи и т.п.

В основе операционного метода лежит системный подход к решению задач – последовательное усложнение задачи до тех пор, пока не будут введены в рассмотрение все существенные взаимосвязи. При этом на каждом этапе решается задача определения условного экстремума.

Учитывая сложность теории оптимального проектирования, в настоящем курсе рассматриваются отдельные узкие задачи, каждая из которых возникает при совместном рассмотрении двух-трех основных требований проектирования. Подобные задачи будем называть задачами оптимального проектирования конструкций, так как их цель состоит в получении наилучшего проектного решения при учете противоречивых требований проектирования. При этом наибольшее внимание будем уделять задачам о минимуме веса или стоимости несущей конструкции при обеспечении условий надежности.

В настоящее время в Росси и за границей стала широко применяться система автоматизированного проектирования (САПР) строительных конструкций, основанного на теории оптимального проектирования. Эта система САПР представляет сложный комплекс тесно связанных в своих действиях людей – специалистов и автоматических машин (вычислительных, видеовоспроизводящих, оформляющих, осуществляющих передачу информации и связь, хранящих справочные данные и результаты предшествующего проектирования). Использование САПР позволяет существенно усовершенствовать общие методы рационального проектирования строительных конструкций с учетом их существенных индивидуальных особенностей.

 

ТЕМА 2. ПОСТАНОВКА НЕКОТОРЫХ ОСНОВНЫХ ЗАДАЧ ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ

Задача оптимизации - определение значения переменных x₁,…, x_i,…,x_{n ,}, при которых функция F(x₁,…, x_i,…,x_n) принимает минимальное или максимальное значение.

Функция F(x₁,…, x_i,…,x_n) называется целевой функцией.

Переменные x₁,…, x_i,…,x_n называются параметрами управления

Физическая или технико-экономическая величина, которая определяется ее значениями (вес, стоимость, трудоемкость и т.п.), называется критерием оптимальности.

Критерий оптимальности и целевая функция понятия различные и их нельзя путать. Выбор критерия оптимальности и формирование соответствующей ему целевой функции – различные этапы постановки задачи оптимального проектирования.

Если на переменные x₁,…, x_i,…,x_n не наложены никакие ограничения, то это задача определения безусловного экстремума целевой функции.

Если на переменные x₁,…, x_i,…,x_n наложены ограничения, то это задача определения условного экстремума целевой функции.

Ограничения, налагаемые на переменные, по смыслу задачи могут иметь вид равенств

g_s=(x₁,…, x_i,…,x_n) =0 (s=1, 2,…,p) (6)

илинеравенств

y_t(x₁,…, x_i,…,x_n) ≥ 0; (t=1, 2,…q). (7)

Кроме того, некоторые и переменных или все переменные могут иметь ограничения по знаку x_j ≥ 0 (j=1, 2,… k; k ≤ n). (8)

Помимо переменных x₁,…, x_i,…,x_n в уравнения связи (6) и ограничения (7) могут входить другие переменные величины, называемые параметрами состояния.

Изменяя параметры управления, можно изменять состояние системы, т.е. управлять как бы этим состоянием.

 

Целевая функция.

Рассмотрим задачи о построении целевой функции при различных критериях оптимальности на примере стержневых конструкций. В качестве стержневой конструкции примем стропильную ферму.

Металлические конструкции.

При оптимальном проектировании металлических конструкций за критерий оптимальности принимают вес основных несущих элементов (полок и стенки балок, стержней ферм, ветвей колонн и т.п.), вес основных несущих элементов и конструктивных деталей (фасонок, ребер жесткости, соединяющих пластин и т.п.).

Критерий минимума массы позволяет не только установить оптимальное количество материала, необходимого для изготовления конструкций, уменьшить массу, но и оценить, насколько близки или далеки от систем, оптимальных по массе, применяемые в настоящее время в практике строительства традиционные конструкции.

При этом сложность целевой функции зависит от полноты используемого критерия оптимальности.

Покажем построение целевой функции на примере стальной стропильной фермы.

Если в качестве критерия оптимальности принять вес только основных несущих элементов (стержней поясов и решетки), то структура целевой функции будет наиболее простой:

_{k k k}

G = Σ ρ_iA_iℓ_i = ρ Σ A_iℓ_i = Σ w_iℓ_I, (кН) (9)

^{i=1 i=1 i=1}

где ρ_{i -} плотность материала, для стали ρ = 78,5 кН/м³ = const;

A_i, ℓ_i - площадь сечения (м²) и длина (м) стержней фермы;

w_i = ρ A_i (кН/м) – погонный вес стержней фермы;

k – число стержней фермы;

G – функция веса.

Если в качестве критерия оптимальности принять вес основных несущих элементов и конструктивных деталей, то целевая функция усложнится, так как количество критериев оптимальности увеличилось. Для упрощения вес деталей фермы (фасонок, накладок и т.п.) примем приближенно в виде конструктивного коэффициента ψ_i, для каждого стержня фермы:

_{k k k}

G = Σ ρ_iA_iℓ_i ψ_i = ρ Σ A_iℓ_i ψ_i = Σ w_iℓ_I ψ_i, (кН) (10)

^{i=1 i=1 i=1}

Железобетонные конструкции.

При оптимальном проектировании железобетонных конструкций за критерий оптимальности принимают суммарную стоимость бетона и продольной арматуры.

Для стропильной железобетонной фермы из элементов прямоугольного сечения стоимость конструкции определяется следующим выражением

_k

С = Σ (с_b A_biℓ_i + c_s ρ A_siℓ_i), (кН) (11)

ⁱ⁼¹

где A_bi = bh – площадь сечения стержня (м²);

ℓ_i - длина элемента фермы (м);

с_b - стоимость 1м³ бетона (руб/ м³);

c_s - стоимость 1п.м арматуры (руб/м);

ρ - объемный вес арматурной стали (кН/м³);

A_si – площадь сечения рабочей арматуры (м²).

Ограничимся приведенными примерами. Аналогично можно составить целевые функции веса или стоимости для различных конструкций. Основная трудность состоит не в формировании целевой функции, когда критерий оптимальности уже выбран, а в правильном выборе самого критерия.

Структура целевой функции часто определяет способ решения задачи. Например, для задачи, где используется функция стоимости (11), отыскания оптимальных параметров конструкции рационально использовать метод последовательных приближений.

 

Ограничения – неравенства.

При проектировании стержневых конструкций редко встречается тот элементарный случай, когда рассматривается статически определимая система и требования надежности представлены только условиями прочности. В этом случае абсолютный минимум веса имела бы равнопрочная конструкция

(например равнопрочная консольная балка) и условия прочности можно было бы задать в виде равенств.

Помимо условий прочности, обычно приходится учитывать условия устойчивости и жесткости, конструктивные и технологические ограничения. При этом заранее неизвестно, из всех этих условий и в каком сочетании будут лимитировать оптимальные поперечные размеры элементов.

Условие прочности вводится в математическое описание задач оптимального проектирования в виде неравенств. Если алгебраический знак усилия заранее не известен, то каждое условие прочности записывается в виде двойного неравенства, что эквивалентно ограничению абсолютной величины расчетного сопротивления.

Например, условия прочности на изгиб могут иметь такой вид:

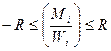(12)

где R – расчетное сопротивление материала;

M_i – изгибающий момент в расчетном сечении i-того стержня;

W_i – момент сопротивления сечения i-того стержня.

Для стержня, испытывающего осевую деформацию, помимо требований прочности, учитывают требования устойчивости

(13)

где R – расчетное сопротивление материала;

N_i – продольная сила в расчетном сечении i-того стержня;

А_i – площадь сечения i-того стержня;

φ_i – коэффициент продольного изгиба.

Условие жесткости записывается также в виде неравенства

f_i ≤ [f] (14)

где f_i – перемещение (например, прогиб), которое требуется ограничить;

[f] – величина предельного перемещения.

В задачах оптимального проектирования строительных конструкций типы сечений стержней обычно назначают заранее, поэтому в некоторых случаях можно получить прямую зависимость, связывающую некоторые величины: гибкость стержня и площадь поперечного сечения, момент инерции площадь поперечного сечения и т.п.

Для этого, задав несколько значений, например гибкости в ожидаемом диапазоне ее изменения, следует скомпоновать рациональное сечение выбранного типа для каждого значения гибкости (длина стержня). Возможный диапазон гибкости для каждого стержня обычно известен. Поэтому нетрудно связать аналитической зависимостью гибкость и коэффициент продольного изгиба (если диапазон невелик, то это будет линейная функция). В результате можно выразить коэффициент φ_i непосредственно через площадь поперечного сечения А_i. Это удобно, потому что в целевую функцию обычно входят площади А_i, которые и требуется определить. Также через площадь поперечного сечения можно выразить момент сопротивления и момент инерции.

Если выбранный тип сечения достаточно прост (прямоугольное сечение, кольцевое или коробчатое сечение) то за параметры управления удобно принять не площади поперечных сечений, а непосредственно поперечные размеры стержня и размеры элементов его сечения. Все остальные расчетные характеристики будут тогда выражены через них.

Уравнения состояния.

Силовое и деформированное состояние несущей конструкции как физическое явление можно исследовать исчерпывающим образом, если рассмотреть три стороны этого явления: статическую (в общем случае динамическую), геометрическую и физическую, определяющую уравнения состояния материала.

Именно такое раздельное исследование уместно делать при постановке задачи оптимального проектирования конструкций. Действительно выбор основных неизвестных среди параметров состояния и соответствующее этому выбору последующее преобразование исходных уравнений состояния в каждой задаче может быть достаточно индивидуальным.

Правильный выбор основных неизвестных и удачное преобразование уравнений могут существенно упростить математическое описание задачи. С помощью канонических уравнений и матричных алгоритмов строительной механики можно получить конечные зависимости между параметрами состояния и параметрами управления, целесообразные для определения силового и деформированного состояния при заданных жесткостях стержней. Однако эти зависимости достаточно сложны и далеко не всегда пригодны для задач оптимизации.

Задача оптимального проектирования конструкций в принципе значительно сложнее и шире, чем задача строительной механики. Она требует более глубокого анализа уравнений состояния. Вот почему привычная форма методов строительной механики стержневых систем не всегда оказывается удобной в задачах оптимального проектирования.

При статической нагрузке уравнения состояния конструкции включает в свой состав три группы уравнений: уравнения равновесия, геометрические соотношения и физические зависимости.

Например, для статически неопределимой фермы при узловой нагрузке уравнения состояния будут иметь вид:

Система уравнений равновесия в матричном виде

D N = B P (15)

где N – столбец неизвестных усилий в стержнях фермы;

P – столбец узловой нагрузки;

D, B – матрицы соответствующих коэффициентов;

Система геометрических уравнений в матричном виде

ε = С U (16)

где ε = столбец деформаций стержней;

С – столбец перемещений узлов;

U – матрица соответствующих коэффициентов.

Систему физических уравнений можно представить в виде следующей матричной формулы

N = Е А ε (17)

где Е – модуль деформации;

А - диагональная матрица, в которой записаны площади поперечных сечений стержней.