Явление рассеяния света лежит в основе ряда оптических методов определения концентрации частиц дисперсной фазы и размеров частиц: ультрамикроскопии, нефелометрии, турбидиметрии /I, с. 260 – 265/.
Ультрамикроскопия отличается от обычной микроскопии боковым освещением дисперсной системы, при этом наблюдают свет, рассеянный отдельными частицами. На темном фоне они кажутся отдельными светящимися точками. Кажущийся диаметр частицы равен сумме ее действительного диаметра и разрешающей силы микроскопа. Метод позволяет рассчитывать число частиц, определять их размер (до 2 – 3 нм) и наблюдать движение частиц. В современных приборах все операции автоматизированы. Одной из отечественных разновидностей таких приборов является поточный ультрамикроскоп Б.В. Дерягина и Г.Я. Власенко. Вспышка отдельных частиц, проходящих в потоке золя по освещенной зоне, регистрируется счетчиком.
Метод нефелометрии основан на измерении интенсивности света, рассеянного коллоидным раствором. Метод применяют для определения концентрации и размеров частиц, и реже – их формы. Для этой цели используют нефелометры /I, с. 265/. Определение частичной концентрации золя основано на пропорциональности интенсивности света, рассеянного некоторым объемом коллоидного раствора 
, общему числу рассеивающих частиц в данном объеме, 
.
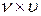Уравнение Рэлея представляют в виде
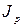
, где (4)
k - константа, объединяющая все параметры в уравнении (2), остающиеся постоянными.
При = const:
Јр1/Јр2=ν1 / ν2 (5)
При ν = const:
Јр1/Јр2 = 1/ 2 = d13/d23 (6)
Таким образом, имея стандартные золи (или градуировочные кривые), можно определить размер частиц или частичную концентрацию золя.
Метод нефелометрии широко используется для определения молярной массы макромолекул /I, с. 263 - 264/.
|
|
Турбидиметрия основана на измерении интенсивности света, прошедшего через дисперсную систему.
Изменение интенсивности света, проходящего через любую среду, подчиняется закону Ламберта – Бера:
Jп=J0 e-τι, (7)
где Jп – интенсивность прошедшего света;
J0 – интенсивность падающего света;
ι – толщина слоя среды;
τ – экстинкция, или коэффициент ослабления.
При ослаблении луча света τ > 0. К средам, в которых τ < 0 относятся лазерные среды. Причинами ослабления луча света могут быть рассеяние света или его поглощение. Поглощение света может происходить при переходе световой энергии в тепловую (абсорбция света), химическую энергию (фотохимические реакции), электрическую (фотоэлементы) и в другие виды энергии.
Если ослабление луча света происходит в результате рассеяния света, то коэффициент τ характеризует способность системы рассеивать свет и называется мутностью. Если изменение интенсивности света обусловлено его абсорбцией, то τ характеризует способность системы поглощать свет и называется коэффициентом поглощения. Употребляется также и название, данное под уравнением (7).
Считая рассеянный свет фиктивно поглощенным, мутность связывают с оптической плотностью коллоидного раствора D:
(8)
где Jп – интенсивность света, прошедшего через систему; D=lgJ0/Jп – оптическая плотность; τ – мутность; l – толщина слоя коллоидного раствора.
Из уравнения (8) следует, что мутность имеет размерность м-1, см-1, нм-1, т.е. единица длины в минус первой степени. Её физический смысл можно определить как величину, обратную расстоянию, на котором интенсивность света снижается в е раз.
|
|
Интенсивность прошедшего света Jп можно представить как разность между интенсивностью падающего света и интенсивностью света, рассеянного слоем коллоидного раствора толщиной l:
JП = J0 –Jpl (9)
тогда
(10)
Применим формулу разложения логарифма в ряд:
lnx=(x-1) - (x-1)2/2 + (x-1)3/3 – (x-1)4/4 +..., при условии 0 < x ≤ 2.
Ограничиваясь при этом первым слагаемым, и пренебрегая малыми величинами второго порядка, получим:
D= Jpl/(J0 – Jpl)≈Jpl/J0 =(Jp/J0)l, (11)
так как Jpl << J0 .
Сравнение уравнений (8) и (11) показывает, что мутность может быть определена как отношение интенсивностей рассеянного и падающего света при толщине слоя коллоидного раствора l равной единице. В то же время, это отношение может быть выражено и из уравнения Рэлея. Объединяя постоянные величины в уравнении Рэлея одной константой K, получим:
(12)
Из уравнения (12) следует, что при одной и той же концентрации частиц дисперсной фазы, оптические плотности двух коллоидных растворов, измеренные при одной длине волны падающего света, относятся как объёмы частиц или как кубы их радиусов, а при одинаковых размерах частиц, как частичные концентрации этих растворов. Эти зависимости используются в методе турбидиметрии для определения размеров частиц и их концентрации.
Приборы, служащие для измерения оптической плотности растворов, называются фотоэлектроколориметрами. Поскольку оптическая плотность раствора (а следовательно и τ) зависит от длины волны, то используется монохроматическое излучение (фотоэлектроколориметры снабжены светофильтрами) и обязательно указывается длина волны, при которой определена оптическая плотность, Dλ.
|
|
Для расчета радиуса частиц сферической формы при 
, принимая Θ=90о, из уравнения Рэлея (2) получают:
(13)
Уравнение (13) используют при работе с "белыми золями" малых концентраций. При этом содержание дисперсной фазы в коллоидном растворе (ν) должно быть известно. Методом последовательных разбавлений готовят серию растворов с известными значениями концентраций частиц ν и измеряют с помощью фотоэлектроколориметра их оптическую плотность, используя красный светофильтр. По уравнению (8) рассчитывают мутность растворов τ и строят график в координатах τ/ν - ν. Экстраполяцией находят по графику значение τ/ν при ν=0. Подставляя полученное значение в уравнение (13), рассчитывают радиус частиц. Длину волны в данной среде λ рассчитывают как λвак/no, где no =1,333 – показатель преломления воды, являющейся дисперсионной средой.
Чаще приходится иметь дело с растворами, в которых размер частиц превышает пределы применимости закона Рэлея.