Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны

Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет

Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны

Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.

Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.

· точка A лежит на прямой a, тогда это имеет такую форму записи A∈a.

· точка А не принадлежит, тогда другая запись A∉a.

· Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.

· Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.

· Любая точка O, находящаяся на прямой, делит ее на два луча, причем две любые точки одного луча лежат по одну сторону луча относительно точки O, а другие – по другую сторону луча.

· Две прямые на плоскости могут совпадать.

· Две прямые на плоскости могут пересекаться. (Если имеется форма записи a∩b=M, то отсюда следует, что заданные прямые a и b пересекаются в точке M.)

· Две прямые на плоскости могут быть параллельны. (если две заданные прямые не имеют общих пересечений, а, значит, и точек, они параллельны,то можно записать a∥b.

Две прямые называют скрещивающимися, при условии, что они не лежат в одной плоскости.

Если две прямые лежат в одной плоскости, угол между ними легко измерить — например, с помощью транспортира. А как измерить угол между прямой и плоскостью?

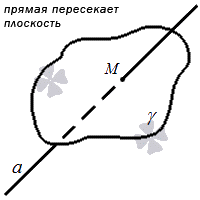
Прямая и плоскость пересекаются в том случае, когда они имеют одну общую точку, то есть она является точкой пересечения прямой и плоскости.

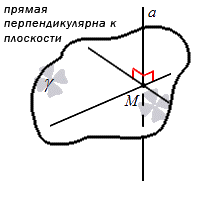
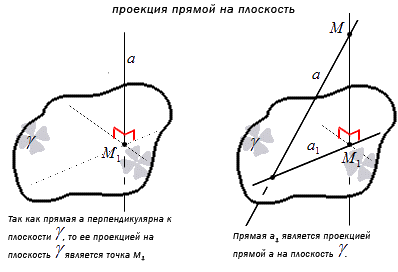
Прямая является перпендикулярной к плоскости, когда она перпендикулярна любой прямой, находящейся в этой плоскости.

Углом между прямой и плоскостью называют угол между этой прямой и ее проекцией на эту плоскость, причем прямая не перпендикулярна к ней.

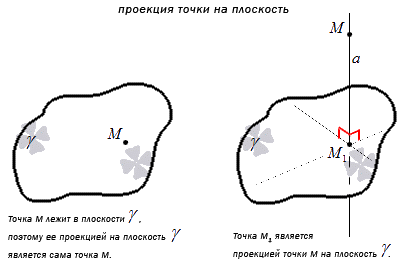
Проекция точки M на плоскость γ является сама точка, если она лежит в заданной плоскости, либо является точкой пересечения плоскости с прямой, перпендикулярной плоскости γ, проходящей через точку M, при условии, что она не принадлежит плоскости γ.

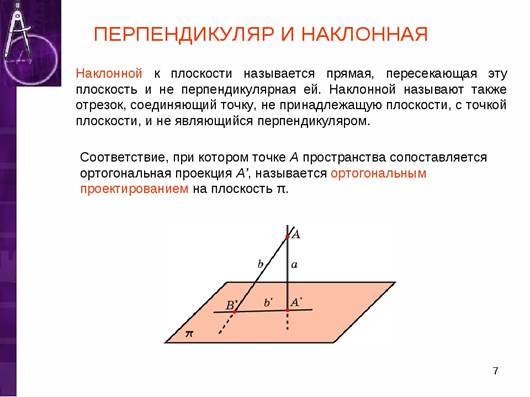
Проекция прямой а на плоскость γ - это множество проекций всех точек заданной прямой на плоскость.(Опустим перпендикуляр из какой-либо точки наклонной на нашу плоскость. Соединим основание перпендикуляра с точкой пересечения наклонной и плоскости. Мы получили проекцию наклонной на плоскость.)

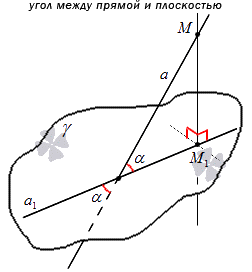
Углом между прямой и плоскостью называют угол между этой прямой и ее проекцией на эту плоскость, причем прямая не перпендикулярна к ней.

признак перпендикулярности прямой и плоскости:

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.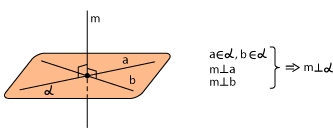

Замечания.

1. Если прямая параллельна плоскости, то расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.

2. Если две плоскости параллельны, то расстояние от произвольной точки одной из плоскостей до другой называется расстоянием между данными плоскостями.

3. Если две прямые скрещиваются, то расстояние между одной из этих прямых и плоскостью, проведённой через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

Теорема о трёх перпендикулярах. Прямая, проведённая в плоскости через основание наклонной перпендикулярно к её проекции, перпендикулярна и к самой наклонной.

Обратная теорема. Прямая, проведённая в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к её проекции.

Пример №1 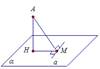Рис. 2

= = Пусть прямая а лежит в плоскости α (рис. 2),

точка А лежит вне плоскости α

Пусть прямая АН перпендикулярна плоскости α,

АМ – наклонная к плоскости α,

НМ – проекция наклонной АМ на плоскость α.

Тогда:

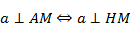
Заметим, что прямая а перпендикулярна плоскости АМН.

Пример №2 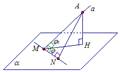Рис. 3

= = Рассмотрим плоскость α и прямую a = АМ,

АН – перпендикуляр,

МН – проекция прямой АМ на плоскость α (рис. 3).

Угол между прямой АМ и плоскостью α – это угол между прямой АМ и ее проекцией МН,

т. е. угол НМА = φ₀. Обозначение: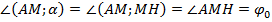

Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.