Актуальность темы.
Одним из важнейших понятий математического анализа есть понятие предела функции. Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.
Цели занятия:
Образовательные цели:
· рассмотреть понятие предела функции в точке, понятие бесконечно малой и бесконечно большой функции, связь между ними;
· применять полученные знания при решении задач.
Развивающие цели:
· развитие логического мышления;
· развитие математической речи;
· развитие памяти и внимания.
Воспитательные цели:
· развитие навыков вычислительной культуры;
· развитие трудолюбия и аккуратности;
· развитие самостоятельности и настойчивости.
Ход занятия:
I Организационный момент
- дата: _._.2020
II Сообщение темы, целей и основных задач занятия, мотивация учебной и познавательной деятельности
Теория пределов – это один из разделов математического анализа.
Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил в 19 веке француз Огюстен Луи Коши, который дал строгие определения многим понятиям математического анализа и заложил его основы. Он доказал огромное количество теорем математического анализа.Наша задача на сегодня:
Понять, что такое предел.
2. Научиться решать основные типы пределов.
III Актуализация опорных знаний
Повторить способы разложения на множители: вынесение за скобки, группировку, использование формул разложения квадратного трехчлена на множители, формул сокращенного умножения.
|
|
IV Изложение нового материала
План занятия:
1. Определения предела функции в точке.
2. Бесконечно большая и бесконечно малая функция и связь между ними.
3. Теоремы о пределах функции в точке.
4. Решение заданий.
Указания:
Просмотреть видеоуроки
https://youtu.be/jYgmiFB_IWA
https://youtu.be/eS-ZLyWDLv8
https://youtu.be/fa7kuQajmU4
Предел функции в точке.
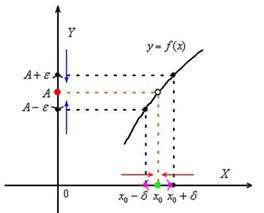
Определение предела функции в точке по Коши: Число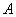 
называется пределом функции 
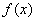в точке х0, если для любой заранее выбранной окрестности 
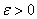(сколь угодно малой), существует 
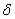-окрестность точки х0, ТАКАЯ, что: КАК ТОЛЬКО значения х (принадлежащие 
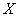) входят в данную окрестность:
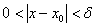(стрелки по оси ОХ) –
ТАК СРАЗУ соответствующие значения функции гарантированно зайдут в
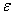-окрестность: 
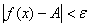(стрелки по оси ОУ).
Записывают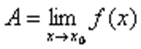 
.
В чём суть определения? Образно говоря, бесконечно уменьшая 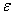-окрестность, мы «сопровождаем» значения функции до своего предела, не оставляя им альтернативы приближаться куда-то ещё.
При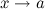 
функция 
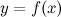может иметь только единственный предел.
Бесконечно малая и бесконечно большая функции
Функция называется бесконечно малой в окрестности точки x 0, если
.
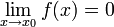Функция называется бесконечно большой в окрестности точки x 0, если
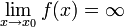
Обратной функцией к бесконечно малой есть бесконечно большая функция и наоборот. Символически это утверждение (не строго математически) можем записать так: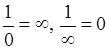 
.