1) 
;
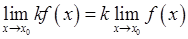2) 
;
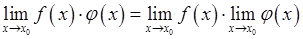3) 
;
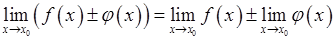4) 
.
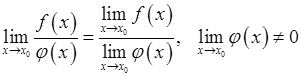При вычислении предела функции под знак предела подставляют значение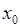 
(
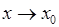) вместо 
.
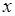Решение заданий.
Пример 1. Вычислить предел функции
.
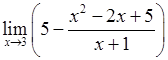Решение. Сама запись читается так: «предел функции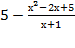 
при х стремящемся к 3». Вместо 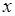подставим число 
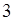под знаком предела. Получим
.
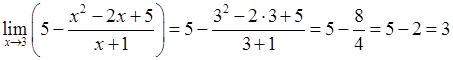Пример 2. Вычислить предел функции
.
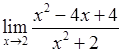Решение. Подставим число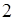 
вместо 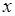и получим
.
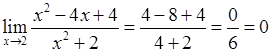Пример 3. Вычислить предел функции
.
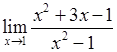Решение. Подставим число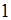 
вместо 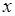и получим:
.
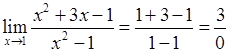Но делить на 0 нельзя! Будем исходить из определения бесконечно малой и большой функций и связи между ними. Тогда выражение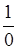 
обозначили “ 
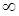”. Это знак предела бесконечно большой функции. Т.е.:
.
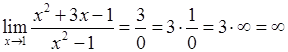Пример 4. Найти предел
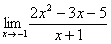
Решение:
Сначала подставим х= -1 в дробь: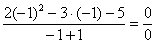 
(*)
В данном случае получена так называемая неопределенность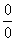 
- отношение двух бесконечно малых величин.
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида 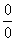, то для ее раскрытия нужно разложить числитель и знаменатель на множители.
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения.
Разложим числитель и знаменатель на множители
Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:
.
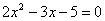
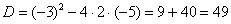
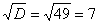! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.
Далее находим корни:
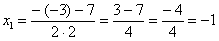
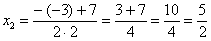
Таким образом:
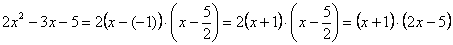
Числитель на множители разложен.
Знаменатель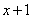 
уже является простейшим множителем, и упростить его никак нельзя.
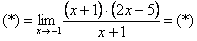
Очевидно, что можно сократить на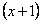 
:
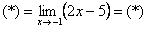
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:
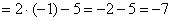
Пример 5. Найтипредел
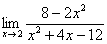
Решение:
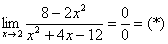
Разложим числитель и знаменатель на множители.
Числитель: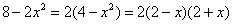 
Знаменатель:
, 
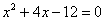
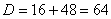
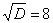
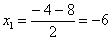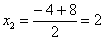
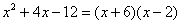
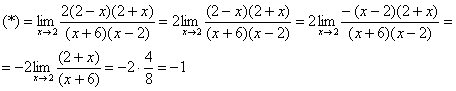
Пример 6. Вычислить предел
.
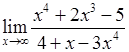Решение. В этом случае получаем неопределенность вида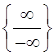 
. Обращаем внимание только на наивысшую степень 
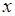, т.е на 
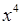. Разделим выражение почленно на наивысшую степень 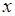и перейдем к вычислению бесконечно малых функций. Имеем:
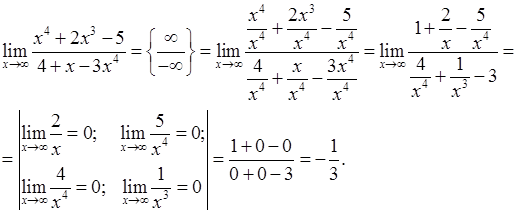
VЗакрепление новых знаний
1) 
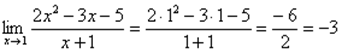
2) 
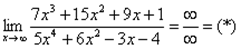Разделим числитель и знаменатель на 
:
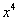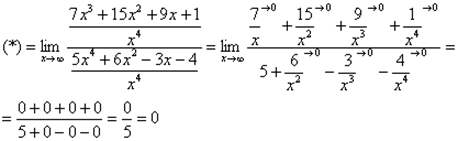
3) 
(*)
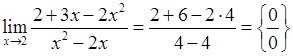для раскрытия неопределенности вида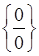 
разложим на множители числитель и знаменатель выражения, а потом сократим на выражение 
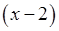. Получим
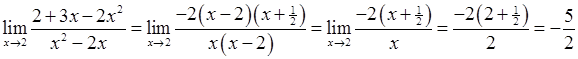= -2,5
VI Подведение итогов занятия
Вопросы для самопроверки:
1. Дать определение предела функции в точке.
2. Какая функция называется бесконечно малой? бесконечно большой?
3. Сформулировать теоремы о пределах.
VII Домашнее задание
1. Конспект занятия, прислать фото.
2. Составить условие и найти пределы (n-номер варианта по списку):
1) 
;
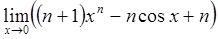2) 
;
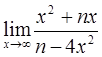3) 
.
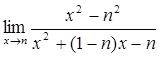Литература основная:
1. Гилярова М.Г. «Математика для медицинских колледжей», Ростов Феникс, 2018
Литература дополнительная:
1. Богомолов Н. В. Математика: учебник для СПО / Н.В. Богомолов, П.И. Самойленко. – 5-е изд., перераб. и доп. – М.: Издательство Юрайт, 2018. – 401 с.
2. Видеоуроки
https://youtu.be/jYgmiFB_IWA
https://youtu.be/eS-ZLyWDLv8
https://youtu.be/fa7kuQajmU4