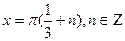Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим.
Чтобы решить простейшие логарифмические уравнения вида 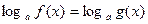 , нужно: 1) решить уравнение
, нужно: 1) решить уравнение 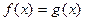 ;
;
2) из найденных корней отобрать те, которые удовлетворяют неравенствам  и
и 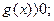 остальные корни уравнения
остальные корни уравнения 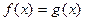 являются посторонними для уравнения
являются посторонними для уравнения  .
.
Определение логарифма и простейшие свойства логарифмов и степеней в разделе «Задания В11:вычисления значений выражений, включающих степени, радикалы, логарифмы и тригонометрические функции» (стр.92).
Пример 25.
В7.Найдите корень уравнения 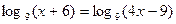 Решение:
Перейдем от заданного уравнения к уравнению х + 6 = 4х – 9, откуда х - 4х = – 9 – 6,
- 3х = – 15, х = 5. Проверку найденного значения х выполним с помощью неравенств
Решение:
Перейдем от заданного уравнения к уравнению х + 6 = 4х – 9, откуда х - 4х = – 9 – 6,
- 3х = – 15, х = 5. Проверку найденного значения х выполним с помощью неравенств 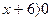 и и 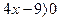 . Число 5 этим неравенствам удовлетворяет. Значит, 5 –корень данного уравнения.
В бланк ответов: В7 . Число 5 этим неравенствам удовлетворяет. Значит, 5 –корень данного уравнения.
В бланк ответов: В7
|
Пример 26.
В7.Найдите корень уравнения  Решение:
Используя свойства
Решение:
Используя свойства  и и 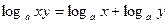 , получим , получим
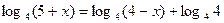 , , 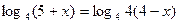 .
Перейдем от полученного уравнения к уравнению 5 + х = 4(4 - х), откуда 5+ х =
= 16 – 4х, 5х = 11, х = 2,2.
Проверку найденного значения х выполним с помощью неравенств 5+ .
Перейдем от полученного уравнения к уравнению 5 + х = 4(4 - х), откуда 5+ х =
= 16 – 4х, 5х = 11, х = 2,2.
Проверку найденного значения х выполним с помощью неравенств 5+ 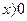 и и 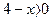 . Число 2,2 этим неравенствам удовлетворяет. Значит, 2,2 –корень данного уравнения.
В бланк ответов: В7 . Число 2,2 этим неравенствам удовлетворяет. Значит, 2,2 –корень данного уравнения.
В бланк ответов: В7
|
Пример 27.
В7.Найдите корень уравнения 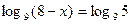 .
Решение:
Перейдем от заданного уравнения к уравнению 8 - х = 5, откуда х = 3. Проверку найденного значения х выполним с помощью неравенства .
Решение:
Перейдем от заданного уравнения к уравнению 8 - х = 5, откуда х = 3. Проверку найденного значения х выполним с помощью неравенства  . Число 3 этому неравенству удовлетворяет. Значит, 3 –корень данного уравнения. . Число 3 этому неравенству удовлетворяет. Значит, 3 –корень данного уравнения.
В бланк ответов: В7 |
Уравнения, примеры 24-35
Пример 28.
В7.Найдите корень уравнения 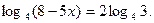 Решение:
Используя свойство логарифмов
Решение:
Используя свойство логарифмов 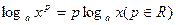 , получим , получим  Перейдем от полученного уравнения к уравнению 8 - 5х = 32, откуда - 5х = 9 – 8, -5х = 1, х = -0,2. Проверку найденного значения х выполним с помощью неравенства Перейдем от полученного уравнения к уравнению 8 - 5х = 32, откуда - 5х = 9 – 8, -5х = 1, х = -0,2. Проверку найденного значения х выполним с помощью неравенства  . Число -0,2 этому неравенству удовлетворяет. Значит, -0,2 –корень данного уравнения. . Число -0,2 этому неравенству удовлетворяет. Значит, -0,2 –корень данного уравнения.
В бланк ответов: В7 |
Простейшее логарифмическое уравнение 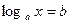 имеет одно решение. Из определения логарифма
имеет одно решение. Из определения логарифма 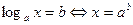 сразу следует, что
сразу следует, что 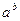 является таким решением.
является таким решением.
Пример 29.
В7.Найдите корень уравнения log 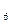 (х-5) = 2.
Решение:
Используя определение логарифма (х-5) = 2.
Решение:
Используя определение логарифма 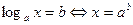 ,получим ,получим
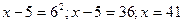 В бланк ответов: В7
В бланк ответов: В7
|
Пример 30.
В7.Найдите корень уравнения log 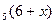 = 2.
Решение:
Используя определение логарифма = 2.
Решение:
Используя определение логарифма 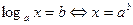 ,получим ,получим
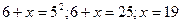 В бланк ответов: В7
В бланк ответов: В7
|
Пример 31.
В7.Найдите корень уравнения log  (8- х) = 2.
Решение:
Используя определение логарифма (8- х) = 2.
Решение:
Используя определение логарифма 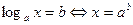 ,получим ,получим
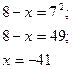 В бланк ответов: В7
В бланк ответов: В7
|
Пример 32.
В7. Найдите корень уравнения log 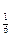 (6-х) = -2.
Решение:
Используя определение логарифма (6-х) = -2.
Решение:
Используя определение логарифма 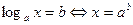 ,получим ,получим
 В бланк ответов: В7
В бланк ответов: В7
|
Уравнения, примеры 24-35
Содержание
Тригонометрические уравнения
Простейшие тригонометрические уравнения cos x = a, sin x = a, tg x = a, ctg x = a
имеют бесконечно много корней.
Решения уравнений по общим формулам:
1) cos x = a, где 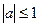 , находят по формуле
, находят по формуле 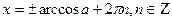 ;
;
2) sin x = a, где 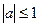 , находят по формуле
, находят по формуле  ;
;
3) tg x = a находят по формуле 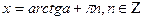 ;
;
4) ctg x = a находят по формуле 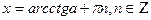 .
.
В некоторых случаях удобнее пользоваться частными формулами:
5) sin x = 0,  6) sin x = 1,
6) sin x = 1, 7) sin x = -1,
7) sin x = -1, 8) cos x = 0,
8) cos x = 0, 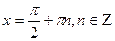 9) cos x = 1,
9) cos x = 1, 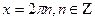 10) cos x = -1,
10) cos x = -1, 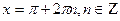 11) tg x = 0,
11) tg x = 0,  12) ctg x =0,
12) ctg x =0, 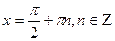
|
Таблица некоторых значений тригонометрических функций дана в разделе «Задания В8: вычисление элементов прямоугольного треугольника» (стр. 63).
Пример 33.
В7. Найдите корень уравнения 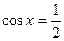 .В ответе запишите наибольший отрицательный корень. Ответ округлите до сотых.
Решение:
Воспользовавшись формулой(1),получим: .В ответе запишите наибольший отрицательный корень. Ответ округлите до сотых.
Решение:
Воспользовавшись формулой(1),получим: 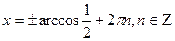 .
Так как .
Так как 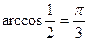 ,то получаем ,то получаем  ; ; 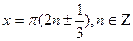 .
Очевидно, что при п = 0 получим наименьший положительный и наибольший отрицательный корни: .
Очевидно, что при п = 0 получим наименьший положительный и наибольший отрицательный корни: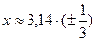 , , 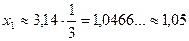 , ,
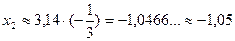 Отсюда наибольший отрицательный корень Отсюда наибольший отрицательный корень 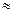 -1,05.
В бланк ответов: В7 -1,05.
В бланк ответов: В7
|
Уравнения, примеры 24-35
Содержание
Пример 34.
В7. Найдите корень уравнения 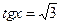 .В ответе запишите наибольший отрицательный корень. Ответ округлите до десятых.
Решение:
Воспользовавшись формулой(3),получим: .В ответе запишите наибольший отрицательный корень. Ответ округлите до десятых.
Решение:
Воспользовавшись формулой(3),получим: 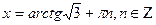 . .
Так как Очевидно, что при п = -1 получим наибольший отрицательный корень, т.е. х
|
Пример 35.
В7. Найдите корень уравнения 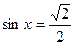 .В ответе запишите наименьший положительный корень. Ответ округлите до десятых.
Решение:
Воспользовавшись формулой(2),получим: .В ответе запишите наименьший положительный корень. Ответ округлите до десятых.
Решение:
Воспользовавшись формулой(2),получим:  .
Так как .
Так как 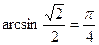 ,то получаем ,то получаем 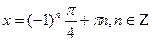 , ,  .
Очевидно, что при п = 0 получим наименьший положительный корень, т.е. х .
Очевидно, что при п = 0 получим наименьший положительный корень, т.е. х  0,785 0,785
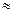 0,8.
В бланк ответов: В7 0,8.
В бланк ответов: В7
|
Пример 36.
В7. Найдите корень уравнения  .В ответе запишите наименьший положительный корень. Ответ округлите до сотых.
Решение:
Воспользовавшись формулой(4),получим: .В ответе запишите наименьший положительный корень. Ответ округлите до сотых.
Решение:
Воспользовавшись формулой(4),получим: 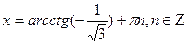 .
Так как .
Так как  ,то получаем ,то получаем 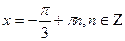 , , 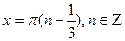 Очевидно, что при п = 1 получим наименьший положительный корень, т.е. х
Очевидно, что при п = 1 получим наименьший положительный корень, т.е. х  2,0933… 2,0933…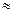
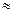 2,09.
В бланк ответов: В7 2,09.
В бланк ответов: В7
|
В7. Найдите корень уравнения  .В ответе запишите наименьший положительный корень. Ответ округлите до сотых.
Решение:
Воспользовавшись формулой(1),получим: .В ответе запишите наименьший положительный корень. Ответ округлите до сотых.
Решение:
Воспользовавшись формулой(1),получим: 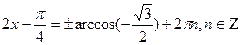 .
Так как .
Так как 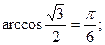 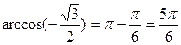 ,то получаем ,то получаем 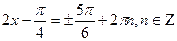 ; ;  ; ; 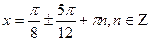 ; ; 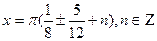 ; ;  .
Очевидно, что при п = 0 получим наименьший положительный и наибольший отрицательный корни: х .
Очевидно, что при п = 0 получим наименьший положительный и наибольший отрицательный корни: х 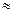 -0,9158...; 1,7008… -0,9158...; 1,7008… 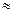 - 0,92; 1,70.
Отсюда наименьший положительный корень - 0,92; 1,70.
Отсюда наименьший положительный корень 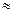 1,70. 1,70.
В бланк ответов: В7 |
Пример 37.
Пример 38.
В7. Найдите корень уравнения 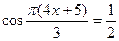 .В ответе запишите наибольший отрицательный корень.
Решение:
Воспользовавшись формулой(1),получим: .В ответе запишите наибольший отрицательный корень.
Решение:
Воспользовавшись формулой(1),получим:  .
Так как .
Так как 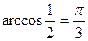 ,то получаем ,то получаем  ; ;  .Умножая обе части уравнения на .Умножая обе части уравнения на 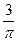 ,получим: ,получим:
 ; ; 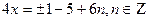 ; ;  .
При п = 1 х = 0; 0,5; при п = 0 х = -1,5; -1. Значит, наибольший отрицательный корень -1.
В бланк ответов: В7 .
При п = 1 х = 0; 0,5; при п = 0 х = -1,5; -1. Значит, наибольший отрицательный корень -1.
В бланк ответов: В7
|
Уравнения, примеры 36-40
Содержание
Пример 39.
В7. Найдите корень уравнения  .В ответе запишите наименьший положительный корень. Ответ округлите до десятых.
Решение:
Преобразуем исходное уравнение: .В ответе запишите наименьший положительный корень. Ответ округлите до десятых.
Решение:
Преобразуем исходное уравнение: ; ; 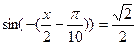 ; ;  ; ; 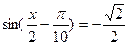 .
Воспользовавшись формулой(2),получим: .
Воспользовавшись формулой(2),получим:  ; ; 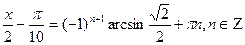 .
Так как .
Так как 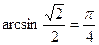 ,то получаем ,то получаем 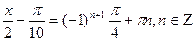 ; ;  ;умножим обе части равенства на 2: ;умножим обе части равенства на 2: 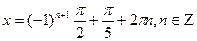 ; ;  .
Очевидно, что при п = 1 получим наименьший положительный корень: .
Очевидно, что при п = 1 получим наименьший положительный корень: 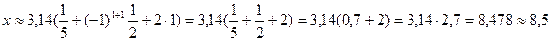 .
В бланк ответов: В7 .
В бланк ответов: В7
|
Пример 40.
В7. Найдите корень уравнения 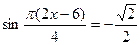 .В ответе запишите наименьший положительный корень.Решение:
Воспользовавшись формулой(2),получим: .В ответе запишите наименьший положительный корень.Решение:
Воспользовавшись формулой(2),получим: 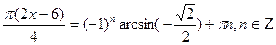 .
Так как .
Так как 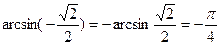 ,то получим ,то получим   ; ; 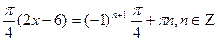 .Умножая обе части уравнения на .Умножая обе части уравнения на 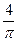 ,получим: ,получим: 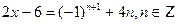 ; ; 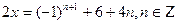 ; ;  .
При п = -2 .
При п = -2 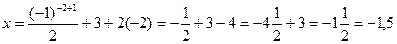 ;
при п = -1 ;
при п = -1 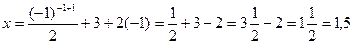 ;
при п = 0 ;
при п = 0 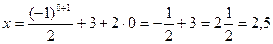 . Значит, наименьший положительный корень 1,5.В бланк ответов: В7 . Значит, наименьший положительный корень 1,5.В бланк ответов: В7
|
Уравнения, примеры 36-40
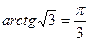 , то получаем
, то получаем 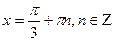 ,
,