Полигон частот. Выборочная функция распределения и гистограмма.

Тема 23. Основные понятия математической статистики. Числовые характеристики

Первичная обработка выборок. Генеральная совокупность и выборка.

Математическая статистика занимается установлением закономерностей, которым подчинены массовые случайные явления, на основе обработки статистических данных, полученных в результате наблюдений. Двумя основными задачами математической статистики являются:

- определение способов сбора и группировки этих статистических данных;

- разработка методов анализа полученных данных в зависимости от целей исследования, к которым относятся:

а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости от других случайных величин и т.д.;

б) проверка статистических гипотез о виде неизвестного распределения или о значениях параметров известного распределения.

Для решения этих задач необходимо выбрать из большой совокупности однородных объектов ограниченное количество объектов, по результатам изучения которых можно сделать прогноз относительно исследуемого признака этих объектов.

Определим основные понятия математической статистики.

Генеральная совокупность – все множество имеющихся объектов.

Выборка – набор объектов, случайно отобранных из генеральной совокупности.

Объем генеральной совокупности N и объем выборки n – число объектов в рассматриваемой совокупности.

Виды выборки:

Повторная – каждый отобранный объект перед выбором следующего возвращается в генеральную совокупность;

Бесповторная – отобранный объект в генеральную совокупность не возвращается.

Замечание. Для того, чтобы по исследованию выборки можно было сделать выводы о поведении интересующего нас признака генеральной совокупности, нужно, чтобы выборка правильно представляла пропорции генеральной совокупности, то есть была репрезентативной (представительной). Учитывая закон больших чисел, можно утверждать, что это условие выполняется, если каждый объект выбран случайно, причем для любого объекта вероятность попасть в выборку одинакова.

Первичная обработка результатов.

Пусть интересующая нас случайная величина Х принимает в выборке значение х ₁ п ₁ раз, х ₂ – п ₂ раз, …, х_к – п_к раз, причем 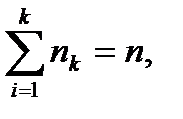где п – объем выборки. Тогда наблюдаемые значения случайной величины х ₁, х ₂,…, х_к называют вариантами, а п ₁, п ₂,…, п_к – частотами. Если разделить каждую частоту на объем выборки, то получим относительные частоты Последовательность вариант, записанных в порядке возрастания, называют вариационным рядом, а перечень вариант и соответствующих им частот или относительных частот – статистическим рядом:

x_i	x ₁	x ₂	…	x_k
n_i	n ₁	n ₂	…	n_k
w_i	w ₁	w ₂	…	w_k

Пример.

При проведении 20 серий из 10 бросков игральной кости число выпадений шести очков оказалось равным 1,1,4,0,1,2,1,2,2,0,5,3,3,1,0,2,2,3,4,1.Составим вариационный ряд: 0,1,2,3,4,5. Статистический ряд для абсолютных и относительных частот имеет вид:

x_i
n_i
w_i	0,15	0,3	0,25	0,15	0,1	0,05

Если исследуется некоторый непрерывный признак, то вариационный ряд может состоять из очень большого количества чисел. В этом случае удобнее использовать группированную выборку. Для ее получения интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько равных частичных интервалов длиной h, а затем находят для каждого частичного интервала n_i – сумму частот вариант, попавших в i -й интервал. Составленная по этим результатам таблица называется группированным статистическим рядом:

Номера интервалов			…	k
Границы интервалов	(a, a + h)	(a + h, a + 2 h)	…	(b – h, b)
Сумма частот вариант, попав- ших в интервал	n ₁	n ₂	…	n_k

Полигон частот. Выборочная функция распределения и гистограмма.

Для наглядного представления о поведении исследуемой случайной величины в выборке можно строить различные графики. Один из них – полигон частот: ломаная, отрезки которой соединяют точки с координатами (x ₁, n ₁), (x ₂, n ₂),…, (x_k, n_k), где x_i откладываются на оси абсцисс, а n_i – на оси ординат. Если на оси ординат откладывать не абсолютные (n_i), а относительные (w_i) частоты, то получим полигон относительных частот (рис.1).

Рис. 1.

По аналогии с функцией распределения случайной величины можно задать некоторую функцию, относительную частоту события X < x.

Определение. Выборочной (эмпирической) функцией распределения называют функцию F* (x), определяющую для каждого значения х относительную частоту события X < x. Таким образом,

, (1)

где п_х – число вариант, меньших х, п – объем выборки.

Замечание. В отличие от эмпирической функции распределения, найденной опытным путем, функцию распределения F (x) генеральной совокупности называют теоретической функцией распределения. F (x) определяет вероятность события X < x, а F* (x) – его относительную частоту. При достаточно больших п, как следует из теоремы Бернулли, F* (x) стремится по вероятности к F (x).

Из определения эмпирической функции распределения видно, что ее свойства совпадают со свойствами F (x), а именно:

1) 0 ≤ F* (x) ≤ 1.

2) F* (x) – неубывающая функция.

3) Если х ₁ – наименьшая варианта, то F* (x) = 0 при х ≤ х ₁; если х_к – наибольшая варианта, то F* (x) = 1 при х > х_к.

Для непрерывного признака графической иллюстрацией служит гистограмма, то есть ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высотами – отрезки длиной n_i /h (гистограмма частот) или w_i /h (гистограмма относительных частот). В первом случае площадь гистограммы равна объему выборки, во втором – единице (рис.2). Рис.2.

Одна из задач математической статистики: по имеющейся выборке оценить значения числовых характеристик исследуемой случайной величины.

Определение. Выборочным средним называется среднее арифметическое значений случайной величины, принимаемых в выборке:

, (2)

где x_i – варианты, n_i - частоты.

Замечание. Выборочное среднее служит для оценки математического ожидания исследуемой случайной величины. В дальнейшем будет рассмотрен вопрос, насколько точной является такая оценка.

Определение. Выборочной дисперсией называется , (3)

а выборочным средним квадратическим отклонением – (4)

Так же, как в теории случайных величин, можно доказать, что справедлива следующая формула для вычисления выборочной дисперсии:

. (5)

Пример 1. Найдем числовые характеристики выборки, заданной статистическим рядом

x_i
n_i

Другими характеристиками вариационного ряда являются:

- мода М₀ – варианта, имеющая наибольшую частоту (в предыдущем примере М₀ = 5).

- медиана т_е - варианта, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно (n = 2 k + 1), то m_e = x_k₊ ₁, а при четном n = 2 k 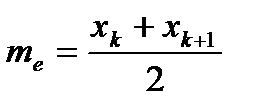. В частности, в примере 1