1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.

где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону
Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа
 где s = 0,926, xср = 0,12
где s = 0,926, xср = 0,12
Теоретическая (ожидаемая) частота равна ni = npi. Вероятность попадания в i-й интервал: pi = Ф(x2) - Ф(x1)
| xi÷xi+1 | ni | x1 | x2 | Ф(x1) | Ф(x2) | pi | Ki |
| -2,42-(-1,94) | -2.7341 | -2.2183 | -0.4969 | -0.4868 | 0.0101 | 0.9703 | |
| -1,94-(-1,46) | -2.2183 | -1.7024 | -0.4868 | -0.4564 | 0.0304 | 0.3031 | |
| -1,46-(-0,98) | -1.7024 | -1.1865 | -0.4564 | -0.383 | 0.0734 | 0.9639 | |
| -0,98-(-0,5) | -1.1865 | -0.6706 | -0.383 | -0.2517 | 0.1313 | 2.8619 | |
| -0,5-(-0,02) | -0.6706 | -0.1548 | -0.2517 | -0.0636 | 0.1881 | 0.7717 | |
| -0,02-0,46 | -0.1548 | 0.3611 | -0.0636 | 0.1443 | 0.2079 | 0.03 | |
| 0,46-0,94 | 0.3611 | 0.877 | 0.1443 | 0.3106 | 0.1663 | 5.2794 | |
| 0,94-1,42 | 0.877 | 1.3929 | 0.3106 | 0.4192 | 0.1086 | 0.0018 | |
| 1,42-1,9 | 1.3929 | 1.9087 | 0.4192 | 0.4719 | 0.0527 | 0.9777 | |
| 1,9-2,38 | 1.9087 | 2.4246 | 0.4719 | 0.4927 | 0.0208 | 0.003 | |
| Сумма | 12.1628 |
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы.
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=2 (параметры xcp и s оценены по выборке).
Kkp = χ2(10-2-1;0.05) = 14.06714; Kнабл = 12,16
Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл < Kkp, поэтому ytn оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют нормальное распределение.
Полигон эмпирических частот и вероятность для нормального распределения.

Сводная таблица проверки гипотез
Таблица 3
| № гипотез | Нулевая гипотеза Н0 | Условная запись нулевой гипотезы | Проверка гипотез | Заключение по гипотезе | |

| 
| ||||
| о нормальности распределения | 
| 12,16, | 14.1 | Гипотеза Yt отвергается | |
| о незначимости асимметрии | 
| 0,57 | 0.72 | Гипотеза не отвергается | |
| о незначимости эксцесса | 
| 0.75 | 1.27 | Гипотеза не отвергается |
Выводы:
Каждое значение ряда отличается от среднего значения 0.12 в среднем на 0.926. Проверка гипотезы по критерию согласия Пирсона показала, что нет оснований отвергать гипотезу о нормальном законе распределения.
Значения As и Ex мало отличаются от нуля. Поэтому можно предположить близость данной выборки к нормальному распределению.
Задание 2. Определение корреляционной зависимости между рядами наблюдений (Регрессионный анализ данных)
В таблице №1 приведены длины сторон  измеренные светодальномером, и их истинные ошибки
измеренные светодальномером, и их истинные ошибки  =
=  .
.
1. Вычислить оценку коэффициента корреляции между приведенными величинами и определить его значимость и надежность;
2. Получить уравнение регрессии (формулу прогнозов) и оценить точность регрессии;
3. Сделать вывод.
Таблица 1
| №№п/п | x i ,(км) | yi , (см) | №№п/п | x i ,(км) | yi , (см)i |
| 7,50 | 5.5 | 6.2 | 5.0 | ||
| 9,70 | 6.5 | 8.5 | 5.0 | ||
| 9,00 | 7.0 | 6.5 | 6.5 | ||
| 7,90 | 4.5 | 2.0 | 2.0 | ||
| 6,10 | 2.5 | 5.3 | 5.0 | ||
| 3.0 | 3.5 | 8.5 | 5.0 | ||
| 3.5 | 2.5 | 4.5 | 2.5 | ||
| 8.1 | 6.0 | 6.7 | 4.0 | ||
| 7.2 | 7.0 | 4.7 | 3.0 | ||
| 5.7 | 5.5 | 7.5 | 5.5 |
План выполнения задания.
1. Построить поле корреляции (точечную диаграмму), изобразив в прямоугольной системе координат точки с координатами, соответствующими каждой паре наблюдений 
2. На основании поля корреляции сделать предположение о наличии между случайными величинами X и Y корреляционной зависимости и о форме этой зависимости (линейная или нелинейная).
3. Вычислить оценки математических ожиданий случайных величин X и Y - средние арифметические 
 и
и  .
.
4. Вычислить оценки средних квадратических отклонений  и
и  .
.
5. Вычислить оценку коэффициента корреляции  - выборочный коэффициент корреляции.
- выборочный коэффициент корреляции.
6. Проверить гипотезу о не значимости коэффициента корреляции.
7. Оценить надежность коэффициента корреляции (критерий Фишера).
8. Получить уравнение регрессии случайной величины Y на X. Нанести прямую линию регрессии на график.
9. Оценить точность регрессии.
10. Выполнить точечную и интервальную оценку точности параметров уравнения регрессии
11. Сделать общий вывод по результатам анализа.
Ход выполнения:
Построим корреляционное поле:

На основании поля корреляции можно предположить существование между величинами Х и Y линейной корреляционной зависимости с функцией регрессии  .
.
Метод наименьших квадратов дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии. Но только в том случае, если выполняются определенные предпосылки относительно случайного члена (ε) и независимой переменной (x).
Формально критерий МНК можно записать так:
S = ∑(yi - y*i)2 → min
Система нормальных уравнений.
an + b∑x = ∑y
a∑x + b∑x2 = ∑yx
Для расчета параметров регрессии построим расчетную таблицу
Таблица 2.
| № | x | y | x2 | y2 | x • y |
| 7,50 | 5,50 | 56,25 | 30,25 | 41,25 | |
| 9,70 | 6,50 | 94,09 | 42,25 | 63,05 | |
| 9,00 | 7,00 | ||||
| 7,90 | 4,50 | 62,41 | 20,25 | 35,55 | |
| 6,10 | 2,50 | 37,21 | 6,25 | 15,25 | |
| 3,00 | 3,50 | 12,25 | 10,5 | ||
| 3,50 | 2,50 | 12,25 | 6,25 | 8,75 | |
| 8,10 | 6,00 | 65,61 | 48,6 | ||
| 7,20 | 7,00 | 51,84 | 50,4 | ||
| 5,70 | 5,50 | 32,49 | 30,25 | 31,35 | |
| 6,20 | 5,00 | 38,44 | |||
| 8,50 | 5,00 | 72,25 | 42,5 | ||
| 6,50 | 6,50 | 42,25 | 42,25 | 42,25 | |
| 2,00 | 2,00 | ||||
| 5,30 | 5,00 | 28,09 | 26,5 | ||
| 8,50 | 5,00 | 72,25 | 42,5 | ||
| 4,50 | 2,50 | 20,25 | 6,25 | 11,25 | |
| 6,70 | 4,00 | 44,89 | 26,8 | ||
| 4,70 | 3,00 | 22,09 | 14,1 | ||
| 7,50 | 5,50 | 56,25 | 30,25 | 41,25 | |
| ИТОГО: | 128,10 | 94,00 | 902,91 | 489,50 | 649,85 |
Для наших данных система уравнений имеет вид

Домножим уравнение (1) системы на (-6.405), получим систему, которую решим методом алгебраического сложения.

Теперь найдем коэффициент «a» из уравнения (1):

Получаем эмпирические коэффициенты регрессии: b = 0.5796, a = 0.9874
Уравнение регрессии (эмпирическое уравнение регрессии):
y = 0.5796x + 0.9874
Построим график уравнения регрессии:

Вычислим основные характеристики
Выборочные средние.



Выборочные дисперсии:


Среднеквадратическое отклонение


Коэффициент корреляции b можно находить по формуле, не решая систему непосредственно:


Ковариация.

Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:

Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < rxy < 0.3: слабая;
0.3 < rxy < 0.5: умеренная;
0.5 < rxy < 0.7: заметная;
0.7 < rxy < 0.9: высокая;
0.9 < rxy < 1: весьма высокая;
В нашем примере связь между признаком Y и фактором X высокая и прямая.
Значимость коэффициента корреляции.
Выдвигаем гипотезы:
H0: rxy = 0, нет линейной взаимосвязи между переменными;
H1: rxy ≠ 0, есть линейная взаимосвязь между переменными;
Если |tнабл| > tкрит — нулевую гипотезу отвергают.

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=18 находим tкрит:
tкрит (n-m-1;α/2) = (18;0.025) = 2.101
где m = 1 - количество объясняющих переменных.
Поскольку |tнабл| > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически – значим
Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:


S2 = 1.111 - необъясненная дисперсия или дисперсия ошибки регрессии (мера разброса зависимой переменной вокруг линии регрессии).

S = 1.05 - стандартная ошибка оценки (стандартная ошибка регрессии).
Sa - стандартное отклонение случайной величины a.


Sb - стандартное отклонение случайной величины b.

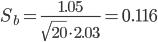
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b - tкрит Sb; b + tкрит Sb)
(0.58 - 2.101*0.116; 0.58 + 2.101*0.116)
(0.336;0.824)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a - tкрит Sa; a + tкрит Sa)
(0.987 - 2.101*0.78; 0.987 + 2.101*0.78)
(-0.652;2.627)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигаем нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R2=0 на уровне значимости α.
2. Далее определяем фактическое значение F-критерия:

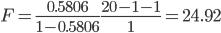
4. Табличное значение критерия со степенями свободы k1=1 и k2=18, Fтабл = 4.41
Поскольку фактическое значение F > Fтабл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна).
Выводы.
Изучена зависимость Y от X. На этапе спецификации была выбрана парная линейная регрессия. Оценены её параметры методом наименьших квадратов. Статистическая значимость уравнения проверена с помощью коэффициента детерминации и критерия Фишера. Установлено, что в исследуемой ситуации 58.06% общей вариабельности Y объясняется изменением X. Установлено также, что параметры модели статистически не значимы. Возможна экономическая интерпретация параметров модели - увеличение X на 1 ед.изм. приводит к увеличению Y в среднем на 0.58 ед.изм. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. При x=7, Y будет находиться в пределах от 2.77 до 7.32 ед.изм. и с вероятностью 95% не выйдет за эти пределы.
Литература.
1. Нефедова Г.А., Ащеулов В.А. Теория вероятностей и математическая статистика в конспективном изложении. Новосибирск, СГГА, 2006.
2. Вентцель Е.С. Теория вероятностей. - М.: Наука, 1969, 4 изд.
3. Агапов Г.И Задачник по теории вероятности. - М.: ВШ., 1986.
4. Гурский Е.И. Сборник задач по теории вероятностей и математической статистике. -М.: 1975.
6. Лесных Н.Б. Основы теории вероятностей и математической статистики. Теория ошибок измерений / Учебное пособие для студентов заочного факультета.- Новосибирск, изд. СГГА, 1992.