Новосибирск 2018г.
Решение задач по теории вероятности.
Задача №1
Монета подбрасывается три раза подряд. Под исходом опыта будем понимать события:
А = {выпадение “герба”},
= {выпадение “ решетки”}.
1. Построить пространство W элементарных событий опыта.
2. Описать событие В, состоящее в том, что: “решетка” выпала не более двух раз.
3. Вычислить теоретическую вероятность события В.
Решение
1. Построим пространство W элементарных событий опыта.
W 
2. Исходя из того, что решетка по условию задачи выпадает не более двух раз, мы исключаем те случаю, когда решетка выпадает три раза. Следовательно, событие В состоит из следующих элементарных событий:
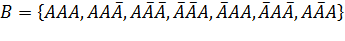
3.Найдем вероятность события В по формуле классической вероятности. Благоприятных исходов 7, а общее количество равновозможных исходов равно W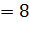 
,
Ответ.
1. W .
2. B 
.
3. 
Задача №2
Для 100 чисел, взятых из исходных данных Контрольной работы № 2, определить относительную частоту и вероятность события, состоящего в появлении (шифр 50)
{ последней цифры два}
| -0.75 | 1.37 | -0.98 | -0.40 | -0.11 | 1.63 | 1.30 | 0.50 | 0.80 | -1.90 | |
| 0.18 | -1.63 | -1.34 | 1.01 | 0.43 | 0.09 | -0.37 | 1.28 | 0.64 | 0.73 | |
| 0.25 | -1.33 | 1.16 | 1.88 | -1.22 | 1.47 | -0.06 | 0.25 | 0.38 | -1.54 | |
| 0.51 | 0.45 | 0.79 | -0.08 | 1.77 | 0.47 | 0.16 | 0.23 | 2.37 | 0.54 | |
| 0.53 | 0.61 | -1.14 | -1.00 | 0.56 | -0.70 | -0.44 | -0.15 | -0.06 | 1.27 | |
| -2.02 | 0.97 | -1.33 | 0.43 | 0.26 | -1.46 | -0.62 | -1.21 | 0.51 | 0.29 | |
| -0.43 | 0.40 | 1.24 | 0.34 | -0.12 | 1.18 | -1.36 | 0.31 | -0.12 | -1.52 | |
| 0.98 | 0.16 | 1.23 | -1.42 | -0.54 | 0.92 | 0.47 | 0.07 | 0.65 | -2.42 | |
| 0.62 | -0.29 | 0.60 | -0.57 | 0.75 | -0.40 | -0.53 | 0.87 | -0.29 | -1.05 | |
| 1.31 | 0.38 | -0.18 | -0.43 | 2.12 | -0.51 | 0.28 | 0.12 | -0.53 | 0.00 |
Решение:
Относительная частота определяется отношением числа испытаний, в которых событие наступило, к общему числу испытаний n=100 m=12
W=0.12
P(A) = 0.1 т.к число 2одно из 10 возможных {0,1,2,3,4,5,6,7,8,9}
Задача №3
В ящике имеется n деталей, среди которых a окрашенных. Наугад вынимают две детали. Найти вероятность того, что:
1) обе извлеченные детали окажутся окрашенными;
2) одна деталь окрашенная, а другая неокрашенная (порядок появления деталей не учитывается);
3) хотя бы одна из двух деталей окажется окрашенной.
У к а з а н и е: значения n и a взять из следующей таблицы согласно номеру варианта:
| Номер варианта | Число деталей | |
| i | n | a |
Решение:
По классическому определению. Событие А – «среди выбранных 2 деталей обе окажутся окрашенными». Событию А благоприятствуют 
элементарных исходов. Всего же элементарных исходов, образующих полную группу событий, равно 
, поэтому:
Пусть событие В – «среди выбранных 2 деталей одна окажется окрашенной, а другая нет». Событию В благоприятствуют 
элементарных исходов. Всего же элементарных исходов, образующих полную группу событий, равно , поэтому:
Пусть событие С – «среди выбранных 2 деталей хотя бы одна окажется окрашенной» (это означает или одна деталь или две будут окрашенные). Событию С благоприятствуют 
элементарных исходов. Всего же элементарных исходов, образующих полную группу событий, равно , поэтому:
Задача №4
Имеются три одинаковые с виду урны. Каждая урна содержит n j белых и m j черных шаров, где j = 1, 2, 3 – номер урны.
1. Найти вероятность того, что вынутый из наудачу взятой урны шар окажется белым.
2. Из наудачу выбранной урны вынули белый шар. Какова вероятность того, что шар вынут из а) первой, б) второй, в) третьей урны?
У к а з а н и е: значения n и m сформировать по данным следующей таблицы (i - номер варианта).
| 1-я урна | 2-я урна | 3-я урна |
n 1 = 1 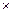 i =10
m 1 = 1+ i=11
| n 2 = 1 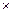i=10
m 2 = 20 - i=10
| n 3 = 5 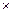i=50
m 3 = 8 + i =18
|
Решение:
1. Пустьсобытие А - «вынутый из наудачу взятой урны шар окажется белым».
Гипотезы:
- «шар из 1 урны»
- «шар из 2 урны»
-«шар и 3 урны»
Найдем вероятности гипотез
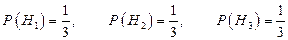
Условные вероятности
По формуле полной вероятности:
имеем
2. Пусть событие А – «из наудачу выбранной урны вынули белый шар». Найдем вероятность того, что шар вынут из а) первой, б) второй, в) третьей урны
Для нахождения вероятностей воспользуемся формулой Байса вероятности:
Задача №5
Батарея произвела 6 выстрелов по объекту. Вероятность попадания в объект при одном выстреле равна 
.
1. Определить вероятность того, что:
а) объект будет поражен k = 0, 1, 2, 3, 4, 5, 6 раз;
б) число попаданий в объект будет не менее трех;
в) число попаданий в объект не более трех;
г) объект будет поражен хотя бы один раз.
2. Получить ряд распределения и построить многоугольник распределения случайной величины X- числа попаданий в объект.
3. Получить функцию распределения случайной величины X и построить ее график.
4. Определить вероятнейшее число попаданий в объект по графику и по формуле.
5. Определить вероятность того, что число попаданий в объект будет заключено в пределах от 2 до 5.
6. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение числа попаданий в объект.
Решение:
а) Пусть A = {батарея поразит объект k раз}. По условию задачи 
. Вероятность того, поражения объекта равна 0,65, следовательно,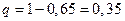 
. По формуле Бернулли имеем:
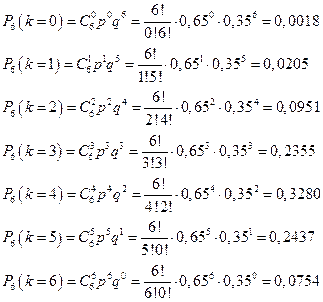
б) число попаданий в объект будет не менее трех
в) число попаданий в объект не более трех
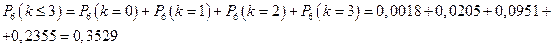
г) объект будет поражен хотя бы один раз.
2. Пусть X- число попаданий в объект
Составим закон распределения данной случайной величины, Х принимает значения 0, 1,2,3,4,5,6.
Таким образом, закон распределения имеет вид
| X | |||||||
| P | 0,0018 | 0,0205 | 0,0951 | 0,2355 | 0,3280 | 0,2437 | 0,0754 |
Построим многоугольник распределения случайной величины X
3. Функцию распределения находим по формуле:
Построим график функции распределения:
4. Определить вероятнейшее число попаданий в объект по графику и по формуле.
По графику данной число равно 4
Число 
называется наивероятнейшим числом наступлений (или наиболее вероятным числом успехов) в схеме Бернулли, если вероятности p и q отличны от нуля то число можно найти из двойного неравенства
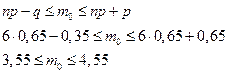
Следовательно, в этом интервале содержится только одно целое число - 4
5. Определить вероятность того, что число попаданий в объект будет заключено в пределах от 2 до 5.
6. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение числа попаданий в объект.
Математическое ожидание:
Дисперсия:
Среднее квадратичное отклонение:
Задача №6
Функция распределения случайной величины Х задана выражением:
Найти:
1) плотность вероятности f(x);
2) математическое ожидание M X;
3) среднее квадратическое отклонение 
;
4) вероятность попадания в интервал (0;5),
Решение:
Так как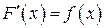 
, то плотность распределения имеет вид
Математическое ожидание вычисляем по формуле 
Дисперсию вычисляем по формуле 
Среднее квадратическое отклонение:
Вероятность того, что случайная величина Х примет значение из интервала [a,b] равна: P(a<x<b) = F(b)- F(a)
Задача №7
Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 10 мм и 2 мм. Найти вероятность того, что:
1). в результате испытания случайная величина Х примет значение, заключенное в интервале (a,b);
2). величина Х примет значение меньше, чем b
| № вар. | a (мм) | b (мм) |
Решение:
Вероятность попадания нормально распределенной случайной величины в заданный интервал определяется формулой:
,
значение функции Лапласа смотрим по таблице.
Следовательно,
1) вероятность того, что случайная величина заключена в пределах от 6 до 10 равна:
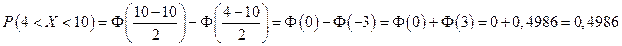2) вероятность того, что величина Х примет значение меньше, чем b
Задача №8
Для случайного вектора 
,
образующего систему случайных величин, известна ковариационная матрица 
, элементы которой каждому студенту следует сформировать на основе матрицы 
, - вычеркнув из нее 10 -ю строку и 10 -й столбец
1.Определить, чему равны средние квадратические отклонения случайных величин X i, входящих в систему.
2. Установить, какие случайные величины X i системы коррелированны, а какие не коррелированы.
3. Получить матрицу коэффициентов корреляции вектора Х91.
Решение:
По диагонали стоят К(Хi,Xi)=M(Xi2)-M(Xi)2=D(Xi), т.е. квадраты среднеквадратических отклонений.
К(Хi,Xi)=D(Xi)=s(Xi) 2
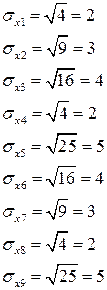
2. Коррелированы могут быть две величины (это означает, что они неким образом зависят друг от друга). Там, где К=0 - некоррелированные величин.
Некоррелированные величины:
X1 и Х3, Х1 И Х4, Х1 И Х8, Х1 И Х9
X2 и Х5, Х2 и Х7, Х2 И Х8
X3 и Х1,, Х3 и Х8,Х3 и Х9
Х4 иХ1, Х4 и Х9
Х5 и Х2,Х5 и Х7, Х5 и Х9
Х6 и Х9
Х7 и Х2, Х7 и Х5, Х7и Х9
Х8 иХ1, Х8 иХ3, Х8 и Х4, Х8 и Х5, Х8 и Х6, Х8 и Х7
Х9 иХ1, Х9 и Х3, Х9 и Х4, Х9 иХ5, Х9 и Х6, Х9 и Х7
3. Коэффициент корреляции равен К(Хi, Xj)/(s(Xi)*s(Xj), где s(Xi) - среднеквадратическое отклонение
Матрица коэффициентов корреляции имеет вид
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | |
| x1 | 1,00 | -0,08 | 0,00 | 0,00 | 0,12 | -0,16 | 0,12 | 0,00 | 0,00 |
| x2 | -0,08 | 1,00 | -0,13 | 0,05 | 0,00 | 0,14 | 0,00 | 0,00 | -0,17 |
| x3 | 0,00 | -0,13 | 1,00 | 0,06 | -0,14 | 0,23 | 0,07 | 0,00 | 0,00 |
| x4 | 0,00 | 0,05 | 0,06 | 1,00 | 0,38 | 0,26 | -0,15 | 0,48 | 0,00 |
| x5 | 0,12 | 0,00 | -0,14 | 0,38 | 1,00 | -0,02 | 0,00 | 0,15 | 0,00 |
| x6 | -0,16 | 0,14 | 0,23 | 0,26 | -0,02 | 1,00 | -0,10 | -0,08 | 0,00 |
| x7 | 0,12 | 0,00 | 0,07 | -0,15 | 0,00 | -0,10 | 1,00 | 0,30 | 0,00 |
| x8 | 0,00 | 0,00 | 0,00 | 0,48 | 0,15 | -0,08 | 0,30 | 1,00 | 0,25 |
| x9 | 0,00 | -0,17 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,25 | 1,00 |
Математическая статистика.
Контрольная работа №2
Исходные данные: результаты измерений 
(i = 1,2,.., n) некоторой случайной величины Х, рассматриваемые как случайная выборка объема 
n из генеральной совокупности; n = 100.
| -0.75 | 1.37 | -0.98 | -0.40 | -0.11 | 1.63 | 1.30 | 0.50 | 0.80 | -1.90 | |
| 0.18 | -1.63 | -1.34 | 1.01 | 0.43 | 0.09 | -0.37 | 1.28 | 0.64 | 0.73 | |
| 0.25 | -1.33 | 1.16 | 1.88 | -1.22 | 1.47 | -0.06 | 0.25 | 0.38 | -1.54 | |
| 0.51 | 0.45 | 0.79 | -0.08 | 1.77 | 0.47 | 0.16 | 0.23 | 2.37 | 0.54 | |
| 0.53 | 0.61 | -1.14 | -1.00 | 0.56 | -0.70 | -0.44 | -0.15 | -0.06 | 1.27 | |
| -2.02 | 0.97 | -1.33 | 0.43 | 0.26 | -1.46 | -0.62 | -1.21 | 0.51 | 0.29 | |
| -0.43 | 0.40 | 1.24 | 0.34 | -0.12 | 1.18 | -1.36 | 0.31 | -0.12 | -1.52 | |
| 0.98 | 0.16 | 1.23 | -1.42 | -0.54 | 0.92 | 0.47 | 0.07 | 0.65 | -2.42 | |
| 0.62 | -0.29 | 0.60 | -0.57 | 0.75 | -0.40 | -0.53 | 0.87 | -0.29 | -1.05 | |
| 1.31 | 0.38 | -0.18 | -0.43 | 2.12 | -0.51 | 0.28 | 0.12 | -0.53 | 0.00 |
План
1. Преобразовать исходную выборку в статистический группированный ряд, построить график эмпирических частот (многоугольник распределения) и выдвинуть гипотезу о нормальном законе распределения генеральной совокупности. Выдвинуть гипотезы об асимметрии и эксцессе кривой распределения.
2. Вычислить теоретические (гипотетические) частоты для каждого интервала группированного ряда. Построить график теоретических частот и вычислить эмпирическое значение критерия согласия Пирсона (критерийc2).
3. Проверить все выдвинутые гипотезы, составить сводную таблицу проверки гипотез и дать заключение по результатам анализа.
Ход выполнения:
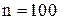- объем выборки;
- максимальный элемент выборки;
- минимальный элемент выборки;
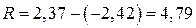- размах выборки;
Примем k = 10 - число интервалов (групп).
Вычислим С = 
- длина интервала (группы).
Определим границы группы.
Таблица 1.
| Номер группы | Нижняя граница | Верхняя граница |
| -2.42 | -1.94 | |
| -1.94 | -1.46 | |
| -1.46 | -0,98 | |
| -0,98 | -0.5 | |
| -0.5 | -0.02 | |
| -0.02 | 0.46 | |
| 0.46 | 0.94 | |
| 0.94 | 1.24 | |
| 1.24 | 1.9 | |
| 1.9 | 2.38 |