Рассмотрим основной геометрический смысл двойного интеграла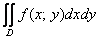 
. Предполагаем, что функция 
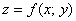существует в каждой точке 
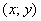плоской области 
и задаёт некоторую поверхность трехмерного пространства. Для определенности считаем, что 
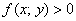, то есть поверхность располагается над плоскостью 
.
Согласно общей концепции интегрирования, произведение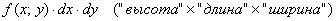 
равно бесконечно малому объёму 
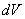элементарного кусочка тела (посмотрите на кусок, выделенный на чертеже пунктирными линиями, и мысленно сделайте бесконечно малыми его «длину» и «ширину»). Двойной же интеграл объединяет эти бесконечно малые значения 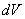по всей области , в результате чего мы получаем суммарный (интегральный) объём всего цилиндрического бруса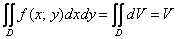 
:
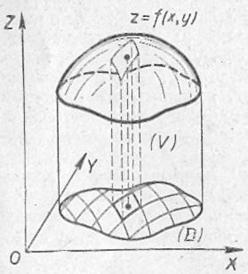
Что это за тело, думаю, понятно – снизу цилиндрический брус ограничен заштрихованной областью , а сверху – фрагментом поверхности 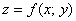(«шапкой»).
Дополнительно поясню геометрический смысл на Примере №1. В нём мы рассматривали двойной интеграл 
, причём область интегрирования имела следующий вид:
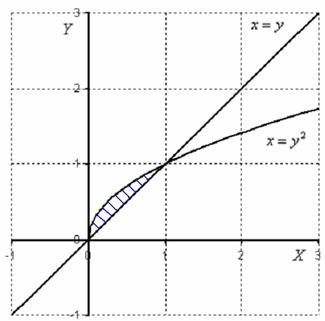
Из начала координат перпендикулярно экрану монитора мысленно проведите на себя стрелку оси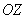 
. Подынтегральная функция 
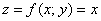задаёт плоскость в пространстве, которая проходит над областью и ограничивает цилиндрический брус сверху, поэтому значение его объёма получилось положительным: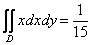 
. Да, такой вот малюсенький брусок, 1/15-я единичного «кубика».
Двойной интеграл может быть и отрицательным, в таких случаях график функции 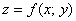полностью (или бОльшей частью) лежит под областью . И если в задаче требуется найти именно объём тела с помощью двойного интеграла (в тройном этот вопрос отпадает), то к «кускам», лежащим ниже плоскости 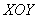, следует добавить знак «минус» (по аналогии с площадью криволинейной трапеции, лежащей ниже оси абсцисс ).
Однако на практике почти всегда встречаются задачи на формальный расчёт двойных интегралов, поэтому мы продолжим совершенствовать технику вычислений:
Пример 3
Вычислить двойной интеграл
, 
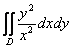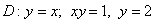
Решение: Изобразим область интегрирования на чертеже:
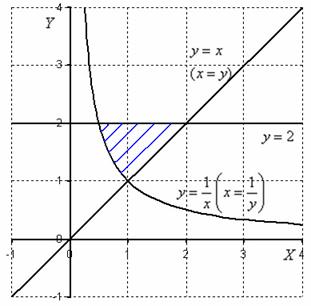
После того, как корректно выполнен чертеж и правильно найдена область интегрирования, самое время разобраться с порядком обхода.
Согласно первому способу обхода, область придется разделить на две части, при этом необходимо будет вычислить следующие интегралы:
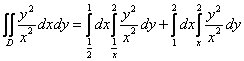
Энтузиазма, прямо скажем, мало. Проанализируем, а не проще ли использовать второй способ обхода области? Перейдем к обратным функциям, переход здесь элементарен:
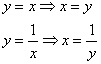
Порядок обхода области:
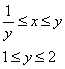
Таким образом:
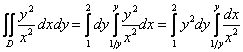
Ну вот, совсем другое дело. И снова заметьте, что во внутреннем интеграле интегрирование осуществляется по «икс», поэтому константу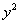 
можно сразу вынести во внешний интеграл
1) Найдём внутренний интеграл:
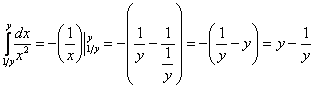
Всё-таки подстановка пределов интегрирования, порой, выглядит своеобразно. Сначала вместо «икса» мы подставили верхний предел интегрирования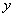 
, затем вместо «икса» подставили нижний предел интегрирования 
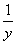. Будьте внимательны при подстановках!
2) Результат предыдущего пункта подставим во внешний интеграл, при этом не забываем про 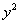, который там уже находится:
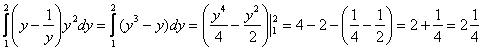
Ответ: 
Для тренировки можете попробовать вычислить двойной интеграл менее рациональным способом: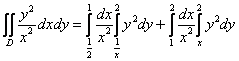 
. Результаты должны совпасть.
Пример 4
Вычислить двойной интеграл
, 
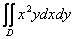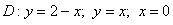
Это пример для самостоятельного решения. Постройте область и проанализируйте, какой способ обхода области выгоднее использовать. Полное решение и ответ в конце урока.
Усложняем задачу, теперь подынтегральная функция будет представлять собой сумму. Рассмотрим еще два примера, где я остановлюсь на приёме вычисления интеграла, который типичен и эффективен для кратных интегралов:
Пример 5
Вычислить двойной интеграл
, 
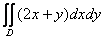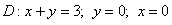
Решение: Сначала рассмотрим то, чего делать не нужно – в данном случае не следует использовать свойства линейности кратного интеграла и представлять его в виде:
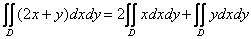
Почему? Вычислений заметно прибавится!
Решение, как обычно, начинаем с построения области интегрирования:
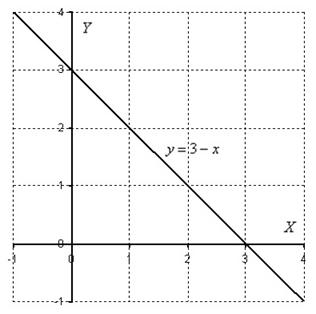
Область незамысловата, даже штриховать не буду. В данном примере, как легко заметить, не имеет особого значения порядок интегрирования, поэтому выберем первый, более привычный вариант обхода области:
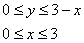
Таким образом:
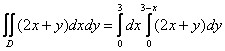
Здесь, в отличие от двух предыдущих примеров, из внутреннего интеграла ничего вынести нельзя, поскольку начинкой является сумма.
С повторными интегралами опять разбираемся по отдельности. Да, кстати, кто хочет посмотреть, как решать повторные интегралы одной строкой, пожалуйста, зайдите на страницу Готовые решения по высшей математике и закачайте архив с примерами решений кратных интегралов.
1) Сначала берём внутренний интеграл:
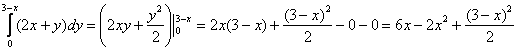
Хотелось бы остановиться на нескольких существенных моментах. Во-первых, о частном интегрировании. О нём я уже подробно рассказывал в статье Дифференциальные уравнения в полных дифференциалах. Вкратце повторюсь:
Если интегрирование проводится по «игрек», то переменная «икс» считается константой. И наоборот.
Тем не менее, вот нашли вы первообразную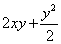 
и возникли сомнения, а правильно ли она найдена? Всегда можно выполнить проверку, в данном случае следует найти частную производную по «игрек»:
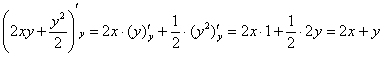
Получена исходная подынтегральная функция, значит, всё в порядке.
Момент второй, подстановка пределов интегрирования. По стандартной формуле Ньютона-Лейбница сначала вместо «игреков» мы подставили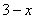 
, а затем – нижний предел интегрирования (нули). После подстановки должны остаться только «иксы».
И, наконец, может показаться странным результат: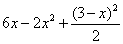 
Ведь можно раскрыть скобки и привести подобные слагаемые! В данном случае это сделать несложно, и чайникам, вероятно, лучше так и поступить. Но если будет не вторая, а 3-я или 4-я степень? На самом деле линейную функцию в степени выгоднее проинтегрировать, не раскрывая скобок! Данный прием я уже применял и подробно комментировал во втором параграфе урока Как вычислить объем тела вращения?
Ещё раз посмотрим, как он работает:
2) Берём оставшийся внешний интеграл:
При нахождении интеграла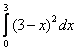 
использован метод подведения функции под знак дифференциала. Где-нибудь возникли сомнения в правильности интегрирования? Возьмите производную по «икс» и выполните проверку!
Ответ: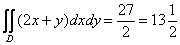 
Пример 6
Вычислить двойной интеграл
, 
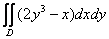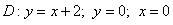
Это пример для самостоятельного решения. В образце решения, как и в разобранном примере, использован первый способ обхода области.
На практике немало примеров, где трудно (а то и невозможно) обойтись без микрокалькулятора-«дробовика». Рассмотрим практический пример на данную тему:
Пример 7
Вычислить двойной интеграл по области 
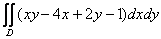
Задача будет решена двумя способами, так как готовое решение у меня уже есть =) А если серьезно, второй способ будет нужен для дополнительных важных комментариев.
Решение: Изобразим область интегрирования на чертеже:
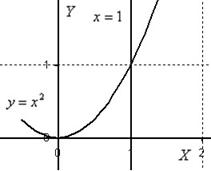
Область интегрирования тут простая, и основной гемор ожидается как раз в вычислениях.
Выберем следующий порядок обхода области:
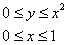
Таким образом:
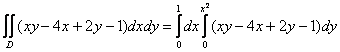
1) 
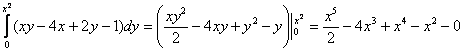
Начинающим чайникам всегда рекомендую выполнять проверку, особенно в подобных примерах: возьмите частную производную по «игрек» от первообразной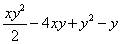 
и получите подынтегральную функцию 
.
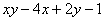Будьте предельно внимательны в подстановке пределов интегрирования: сначала вместо «игреков» подставляем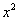 
, затем – ноль. В оформлении вполне допустимо записать один, а не несколько нолей, как это сделано в данном примере. После подстановки должны остаться только «иксы».
2) Второй шаг прост:
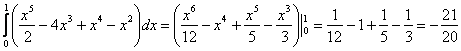
Перейдём к обратной функции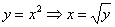 
и изменим порядок обхода области:
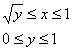
Таким образом:
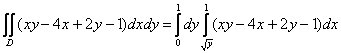
1) Вычислим внутренний интеграл:
Когда мы интегрируем по «икс», то переменная «игрек» считается константой. Не лишней будет и промежуточная проверка, возьмём частную производную по «икс» от найденной первообразной:
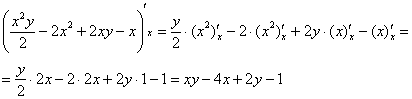
Получена подынтегральная функция, что и хотелось увидеть.
Подстановка пределов интегрирования здесь сложнее: сначала вместо «иксов» подставляем 1, затем вместо «иксов» подставляем 
. После подстановки должны остаться только «игреки».
Степени рекомендую оставить в виде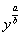 
, а не преобразовывать их в корни – будет удобнее интегрировать на втором шаге:
2)
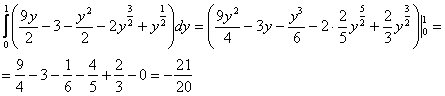
Результаты совпали, как оно и должно быть.
Легко заметить, что первый способ решения был заметно проще.
Всегда перед решением анализируйте – какой путь легче и короче.
Дроби в рассмотренном примере еще худо-бедно можно привести к общему знаменателю вручную. Но не удивляйтесь, если на практике получится ответ вроде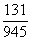 
, по крайне мере, в своей коллекции я нашел немало диких примеров, где без микрокалькулятора-«дробовика» фактически не обойтись.
Ответ: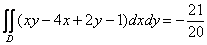 
Ответ получился отрицательным. Геометрически это обозначает, что график подынтегральной функции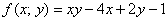 
(поверхность в пространстве) полностью или бОльшей частью (не проверял) располагается ниже области интегрирования под плоскостью .
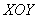Пример 8
Вычислить двойной интеграл по области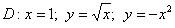 
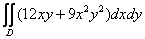
Это пример для самостоятельного решения. Ответ будет целым – чтобы от своего хорошего настроения не запугать вас окончательно =). Похожие двойные интегралы встречаются в известном задачнике Кузнецова, и по этой причине пример тоже уместен. Полное решение и ответ в конце урока.
Студенты-заочники почти всегда сталкиваются с двойными интегралами наподобие тех, которые уже рассмотрены, но никто не застрахован от творческих примеров, где в подынтегральной функции есть какие-нибудь синусы, косинусы, экспоненты и т.п.
Рассмотрим заключительные примеры на данную тему:
Пример 9
Вычислить двойной интеграл по области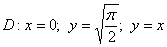 
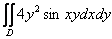
Решение: В ходе выполнения чертежа может возникнуть трудность с построением прямой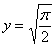 
, которая параллельна оси 
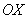. Ничего сложного: если 
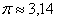, то 
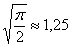– примерно на этом уровне и следует провести прямую.
Выполним чертёж:
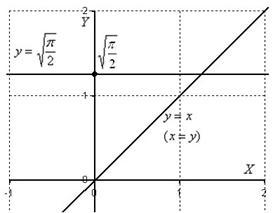
После выполнения чертежа нужно выяснить, какой порядок обхода области выгоднее применить.
Рассмотрим первый способ обхода:
Тогда: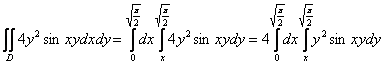 
Очевидно, что первый способ является крайне неудачным, поскольку внутренний интеграл 
придётся дважды брать по частям.
Но есть еще и второй способ обхода области:
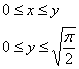
Следовательно: 
Выглядит гораздо привлекательнее, начинаем вычисления:
1) По формуле Ньютона-Лейбница разберемся с внутренним интегралом:
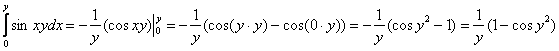
Когда мы интегрируем по «икс», то переменная «игрек» считается константой. Если возникают трудности с интегрированием, можно прибегнуть даже к такому способу: временно замените «игрек» конкретным числом, например, «пятёркой»:
.
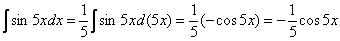Теперь замените «пятёрку» обратно – «игреком»: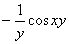 
И, конечно же, лучше сделать проверку, продифференцировав первообразную по «икс»:
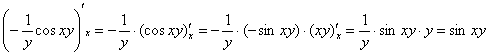
Далее при подстановке пределов интегрирования сначала вместо «икса» подставляем 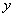, затем – ноль. После подстановки должны остаться только «игреки».
2) Полученный результат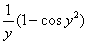 
перемещаем во внешний интеграл, не забывая, что там уже есть 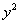и константа 4:
Второй интеграл взят методом подведения функции под знак дифференциала.
Ответ: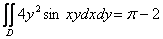 
Таким образом, выбор порядка обхода иногда зависит не только от самой области интегрирования, но и от подынтегральной функции.
Пример 10
Вычислить двойной интеграл по области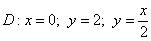 
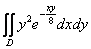
Это пример для самостоятельного решения.
Хочется привести ещё примеры, но в первом раунде я обещал не маньячить, поэтому скрепя сердце, заканчиваю статью. Множество других примеров на вычисление двойных интегралов можно найти в соответствующем архиве на странице Готовые решения по высшей математике. Если тема проработана качественно, то рискну предположить, что многие читатели без особого труда разберутся и и в тройных интегралах – принципы решения очень похожи!