Шайкин А.Н.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕНЫХ
(РЕФЕРАТИВНОЕ ИЗЛОЖЕНИЕ ДЛЯ ВЕЧЕРНЕГО ФАКУЛЬТЕТА)

ПРЕДЕЛ
Определение. Функцией нескольких (n) переменных называется правило f, сопоставляющее каждому упорядоченному набору чисел (x 1, x 2,…, xn) или, другими словами, точке М (М  Х
Х  Rn) некоторое число u
Rn) некоторое число u  R.
R.
Определение. Графиком функции u = f (x 1, x 2,…, xn) называется множество точек пространства Rn +1, координаты которых связаны соотношением u = f (x 1, x 2,…, xn).
Определение. Функция  (M) называется бесконечно малой величиной при М
(M) называется бесконечно малой величиной при М  М 0, если
М 0, если 

 |
|  (M)|<
(M)|<  (
( – проколотая окрестность точки М 0).
– проколотая окрестность точки М 0).
Определение. Число А называется пределом по базе окрестностей точки М 0 функции f (M), т.е. A =  , если f (M)= А +
, если f (M)= А +  (M), где
(M), где  (M) – бесконечно малая величина при М
(M) – бесконечно малая величина при М  М 0, или, развернуто,
М 0, или, развернуто, 

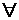 М
М  | f (M)– A |<
| f (M)– A |<  , где
, где  – расстояние между точками М и М 0, которое при М (x 1, x 2,…, xn) и М 0(x 01, x 02,…, x 0 n) вычисляется следующим образом:
– расстояние между точками М и М 0, которое при М (x 1, x 2,…, xn) и М 0(x 01, x 02,…, x 0 n) вычисляется следующим образом:
 =
=  .
.
Теорема (о единственности предела). Если  = А и
= А и  = В, то А = В.
= В, то А = В.
Теорема (об арифметических свойствах предела). Если  = А и
= А и  = В, то для арифметической операции ◊ (◊
= В, то для арифметической операции ◊ (◊  {+,–,
{+,–,  }) имеет место равенство
}) имеет место равенство  ◊ g (M))= A ◊ B (В случае деления необходимо дополнительно потребовать, чтобы В
◊ g (M))= A ◊ B (В случае деления необходимо дополнительно потребовать, чтобы В  0).
0).
Определение. Уравнение М = М 0+ t  называется параметричес-ким уравнением прямой, проходящей через точку М 0 в направлении вектора
называется параметричес-ким уравнением прямой, проходящей через точку М 0 в направлении вектора  .
.
Определение. Число А называется пределом функции f (M) в точке М по направлению l, т.е. А =  , если
, если 

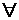 t
t 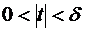 | f (M)– A |<
| f (M)– A |<  .
.
Замечание. Из существования и равенства пределов по всем направлениям, вообще говоря, не следует существования предела по базе окрестностей.
Определение. Пусть f (x, y) определена в проколотой окрестности  точки М 0(х 0, у 0) радиуса R и
точки М 0(х 0, у 0) радиуса R и 
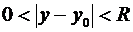
 =
=  . Тогда, если
. Тогда, если  , то он называется повторным пределом. Аналогично определяется повторный предел
, то он называется повторным пределом. Аналогично определяется повторный предел  .
.
Замечание. Если существуют оба повторных предела, то, вообще говоря, b  c. Из существования предела по базе окрестностей, вообще говоря, не следует существования повторных пределов.
c. Из существования предела по базе окрестностей, вообще говоря, не следует существования повторных пределов.
Теорема (о достаточном условии существования повторных пределов). Пусть f (x, y) определена в проколотой окрестности  точки М 0(х 0, у 0) радиуса R и
точки М 0(х 0, у 0) радиуса R и 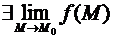 = А. Пусть, кроме того,
= А. Пусть, кроме того, 
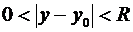
 =
=  и
и 

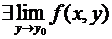 =
=  . Тогда
. Тогда  ,
,  и А = В = С.
и А = В = С.
НЕПРЕРЫВНОСТЬ
Определение. Функция u = f (М) называется непрерывной в точке М 0, т.е.  , если она определена в некоторой окрестности точки М 0 и
, если она определена в некоторой окрестности точки М 0 и  = f (M 0) или
= f (M 0) или  , а развернуто,
, а развернуто, 

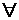 М
М  | f (M)– f(M 0 ) |<
| f (M)– f(M 0 ) |<  .
.
Определение. Функция называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.
Определение. Точка М 0 называется точкой разрыва функции, если функция определена в некоторой проколотой окрестности точки М 0 и в этой точке функция не является непрерывной.
Теорема (об арифметических свойствах функции, непрерывной в точке). Если  и
и  , то для арифметической операции ◊ (◊
, то для арифметической операции ◊ (◊  {+,–,
{+,–,  })
})  ◊ g (M))
◊ g (M))  (В случае деления необходимо дополнительно потребовать, чтобы g (M 0)
(В случае деления необходимо дополнительно потребовать, чтобы g (M 0)  0).
0).
Теорема (о локальной ограниченности функции, непрерывной в точке). Если  , то
, то 
 ,т.е. функция f (М) ограничена в некоторой окрестности точки М 0.
,т.е. функция f (М) ограничена в некоторой окрестности точки М 0.
Теорема (о локальном знакопостоянстве функции, непрерывной в точке). Если  и f (M 0)
и f (M 0)  0, то
0, то
1) f (M 0)> 0 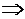

 f (M)> 0;
f (M)> 0;
2) f (M 0)< 0 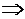

 f (M)< 0.
f (M)< 0.
Определение. Множество называется связным, если любые две его точки можно соединить непрерывной кривой, целиком лежащей в этом множестве.
Определение. Точка М 0 называется предельной для множества Х, если в любой ее окрестности содержатся точки из Х.
Определение. Множество называется замкнутым, если оно содержит все свои предельные точки.
Определение. Множество называется открытым, если для любой точки этого множества существует ее окрестность, содержащаяся в этом множестве.
Теорема. Дополнением замкнутого множества является открытое, а дополнением открытого – замкнутое.
Определение. Множество называется ограниченным, если существует круг с центром в начале координат, содержащий это множество.
Теорема (Коши о промежуточном значении). Если Х – связное множество и  ; М 1
; М 1  Х, М 2
Х, М 2  Х, то для любого значения А, лежащего между f (М 1) и f (М 2) найдется точка М 0
Х, то для любого значения А, лежащего между f (М 1) и f (М 2) найдется точка М 0  Х f (М 0)= А.
Х f (М 0)= А.
Теорема (Вейерштрасса). Если Х – замкнутое и ограниченное множество и  , то
, то  и найдутся точки М 1
и найдутся точки М 1  Х и М 2
Х и М 2  Х, такие что f (М 1)=
Х, такие что f (М 1)=  и f (М 2)=
и f (М 2)=  .
.
ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ И ДИФФЕРЕНЦИРУЕМОСТЬ
Определение. Пусть функция u = f (M) определена на открытом множестве Х и М 0  Х. Пусть М = М 0+ t
Х. Пусть М = М 0+ t  – уравнение прямой, проходящей через точку М 0 в направлении вектора
– уравнение прямой, проходящей через точку М 0 в направлении вектора  (Без ограничения общности, далее будем считать, что |
(Без ограничения общности, далее будем считать, что |  |=1). Тогда f (M)= f (М 0+ t
|=1). Тогда f (M)= f (М 0+ t  )=
)=  . Функция
. Функция  , очевидно, определена при достаточно малом | t |. Если
, очевидно, определена при достаточно малом | t |. Если  дифференцируема по t в нуле, то
дифференцируема по t в нуле, то  называется производной функции f (M) в точке М 0 по направлению вектора
называется производной функции f (M) в точке М 0 по направлению вектора  и обозначается
и обозначается  , т.е.
, т.е.  =
=  .
.
Определение. Если 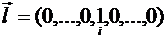 , то
, то  называется частной производной функции f (M) по i -й переменной и обозначается
называется частной производной функции f (M) по i -й переменной и обозначается  .
.
Определение. Пусть функция u = f (M) определена на открытом множестве Х и М 0  Х. Тогда функция u = f (M) дифференцируема в точке М 0, т.е.
Х. Тогда функция u = f (M) дифференцируема в точке М 0, т.е.  , если f (M)= f (M 0)+
, если f (M)= f (M 0)+  ++
++  (M)
(M)  , где
, где  (M) – бесконечно малая величина при М
(M) – бесконечно малая величина при М  М 0 (Можно показать, что
М 0 (Можно показать, что  (M)
(M)  =
=  , где
, где  (M) – бесконечно малые величины при
(M) – бесконечно малые величины при  ).
).
Теорема (достаточное условие существования производных по направлению). Пусть  . Тогда
. Тогда  =
=  (М 0), где
(М 0), где  – коэффициенты из определения дифференцируемости, и
– коэффициенты из определения дифференцируемости, и 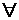


 =
=  .
.
Доказательство. Пусть М = М 0+ t  – уравнение прямой, проходящей через точку М 0 в направлении вектора
– уравнение прямой, проходящей через точку М 0 в направлении вектора  . Тогда приращение функции f (M) в точке М 0 в направлении вектора
. Тогда приращение функции f (M) в точке М 0 в направлении вектора  по определению дифференцируемости будет f (M)– f (M 0)= f (М 0+ t
по определению дифференцируемости будет f (M)– f (M 0)= f (М 0+ t  )– f (M 0)=
)– f (M 0)=  +
+  (М 0+ t
(М 0+ t  )
)  = t
= t 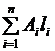 +
+  (t)| t |. Тогда
(t)| t |. Тогда  (M 0)=
(M 0)=  =
=  (
(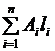 +
+  (t))=
(t))= 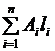 . При
. При 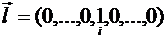 получаем
получаем  (М 0)=
(М 0)=  . Возвращаясь к произвольному
. Возвращаясь к произвольному  , подставляя, получаем
, подставляя, получаем  (M 0)=
(M 0)=  .
.
Замечание. Поскольку li =  , где
, где  – угол между
– угол между  и осью OXi, то для случая трех переменных x, y и z имеем
и осью OXi, то для случая трех переменных x, y и z имеем
 (M 0)=
(M 0)=  (М 0)
(М 0)  +
+  (М 0)
(М 0)  +
+  (М 0)
(М 0)  ,
,
где  ,
,  и
и  – соответствующие направляющие косинусы вектора
– соответствующие направляющие косинусы вектора  .
.
Теорема (необходимое условие дифференцируемости). Если  , то
, то  .
.
Доказательство. Пользуясь определением дифференцируемости, имеем  )=
)=  (
(  +
+  (M)
(M)  )= =
)= =  +
+  =0, что соответствует непрерывности функции f (M) в точке М 0.
=0, что соответствует непрерывности функции f (M) в точке М 0.
Теорема (достаточное условие непрерывности). Пусть функция f (M) определена в некоторой окрестности  точки М 0 и
точки М 0 и 

 (М) (i =1,…, n). Если
(М) (i =1,…, n). Если  (М)
(М)  , то
, то  .
.
Теорема (достаточное условие дифференцируемости). Пусть функция f (M) определена в некоторой окрестности  точки М 0 и
точки М 0 и 

 (М) (i =1,…, n). Если
(М) (i =1,…, n). Если  (М)
(М)  , то
, то  .
.
Доказательство. 

=  –
–  =
=  –
–  +
+
+  –
–  +
+  –…
–…
…–  +
+  –
–  =
=
(по теореме Лагранжа)
= 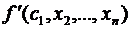
 +
+ 
 +…+
+…+
+ 
 =
=
(по непрерывности частных производных)
= 
 +
+ 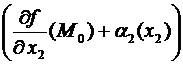
 +…
+…
…+ 
 =
=
= 
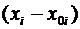 +
+ 
 .
.
Следовательно,  .
.
Замечание. Достаточное условие дифференцируемости не является необходимым, т.е. существуют функции, дифференцируемые в точке, но имеющие разрывные и даже неограниченные в любой окрестности этой точки производные по любому направлению.
ГРАДИЕНТ
Определение. Если на множестве  задана функция f (M),
задана функция f (M),  , то говорят, что на Х задано скалярное поле.
, то говорят, что на Х задано скалярное поле.
Определение. Градиентом скалярного поля (или функции f (M)) в точке М 0 называется вектор  =
= 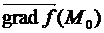 =
=
= 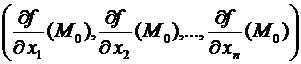 , если
, если  .
.
Замечание. Используя понятие градиента, определение дифференцируемости функции f (M) в точке М 0 можно записать:

 ,
,
а определение производной по направлению:
 .
.
Свойства градиента.
Свойство 1. Производнаяфункции f (M) в точке М 0 по направлению вектора  равна произведению длины вектора
равна произведению длины вектора  на косинус угла
на косинус угла  между векторами
между векторами 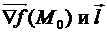 .
.
Доказательство. По определению производной по направлению, градиента и скалярного произведения, учитывая, что  , имеем
, имеем  =
=  =
=  , где
, где  – угол между векторами
– угол между векторами 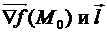 .
.
Свойство 2. Абсолютная величина производнойфункции f (M) в точке М 0 по направлению вектора  не превосходит длины вектора
не превосходит длины вектора  .
.
Доказательство. Поскольку  , то пользуясь свойством 1, получаем
, то пользуясь свойством 1, получаем 

 .
.
Свойство 3. Наибольшее по всем векторам  значение производнойфункции f (M) в точке М 0 по направлению вектора
значение производнойфункции f (M) в точке М 0 по направлению вектора  равно длине вектора
равно длине вектора  , и достигается по направлению вектора
, и достигается по направлению вектора  , где
, где 
 .
.
Доказательство. Пользуясь свойством 1, заметим, что 
 =
=  =
=  и достигается при
и достигается при  , т.е. при
, т.е. при  =0. Следовательно,
=0. Следовательно, 
 .
.
Свойство 4. Наименьшее по всем векторам  значение производнойфункции f (M) в точке М 0 по направлению вектора
значение производнойфункции f (M) в точке М 0 по направлению вектора  равно –
равно –  и достигается по направлению вектора
и достигается по направлению вектора  , где
, где 
 .
.
Доказательство. Пользуясь свойством 1, заметим, что 
 =
= 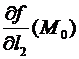 =–
=–  и достигается при
и достигается при  , т.е. при
, т.е. при  =
=  . Следовательно,
. Следовательно, 
 .
.
Свойство 5. Если 

 , то
, то  =0.
=0.
Доказательство. Поскольку 

 , то
, то  =
=  . Тогда
. Тогда  . Следовательно, по свойству 1,
. Следовательно, по свойству 1,  =0.
=0.
Определение. Линией (при n =2) или поверхностью (при n >2) уровня функции f (M), 
 , называется кривая (при n =2) или поверхность (при n >2)
, называется кривая (при n =2) или поверхность (при n >2) 
 , такая что
, такая что  f (M)= const.
f (M)= const.
Свойство 6. Градиент функции f (M) в точке М 0 нормален к линии (поверхности) уровня, проходящей через точку М 0.
Доказательство. Исходя из определения линии (поверхности) уровня, производная функции f (M) в точке М 0 по направлению касательной к линии уровня равна нулю. Следовательно, по свойству 1,  , т.е. угол
, т.е. угол  между касательной к линии уровня и вектором
между касательной к линии уровня и вектором  равен
равен  .
.
Свойство 7. Градиент показывает направление наиболее крутого подъема.
Доказательство. По свойству 3 имеем
 =
= 
 =
=  .
.
Определение. Окружности (сферы), образованные концами всех векторов  при всевозможных векторах
при всевозможных векторах  в конкретной точке М 0 называются индикатрисами производных по направлению функции f (M) в точке М 0.
в конкретной точке М 0 называются индикатрисами производных по направлению функции f (M) в точке М 0.
СЛОЖНАЯ ФУНКЦИЯ
Определение. Пусть  ,
,  . Если
. Если 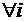
 ,
,  , то
, то  называется сложной функцией.
называется сложной функцией.
Теорема (о производной сложной функции). Пусть о сложной функции, определенной выше, при тех же обозначениях, известно
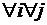
 ;
;  ; (i =1,…, n); (j =1,…, m).
; (i =1,…, n); (j =1,…, m).
Также 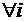
 ;
;  . Тогда
. Тогда  и
и

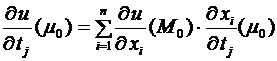 .
.
Доказательство. 


 =
=
=  +
+  , где
, где 
 бесконечно малая величина при
бесконечно малая величина при  . Тогда
. Тогда 
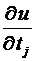 =
=  =
= 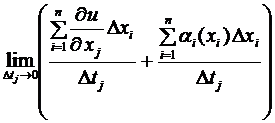 =
=


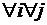

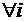
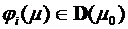

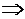

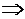

=  =
=  =
=  =
=  .
.
Поскольку 
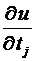 непрерывны как суммы произведений непрерывных функций, то, по теореме о достаточном условии дифференцируемости,
непрерывны как суммы произведений непрерывных функций, то, по теореме о достаточном условии дифференцируемости,  .
.
Частный случай. Пусть  ,
,  ;
; 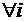
 , т.е.
, т.е.  – сложная функция одной переменной t. Тогда
– сложная функция одной переменной t. Тогда
 .
.
Частный случай частного случая. Если  , где
, где  – одна из
– одна из  , то
, то
 .
.
ДИФФЕРЕНЦИАЛ
Определение. Пусть  , т.е.
, т.е.  (М 0)= =
(М 0)= =  +
+  (M)
(M)  . Тогда дифференциалом функции
. Тогда дифференциалом функции 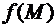 в точке М 0 называется главная, линейная относительно
в точке М 0 называется главная, линейная относительно  часть приращения функции, т.е. df (M 0)= =
часть приращения функции, т.е. df (M 0)= =  .
.
Замечание. 
 =0+…+0+1
=0+…+0+1  +0+…+0=
+0+…+0= 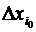 , т.е. дифференциал независимой переменной совпадает с ее приращением. Следовательно, df (M 0)=
, т.е. дифференциал независимой переменной совпадает с ее приращением. Следовательно, df (M 0)=  .
.
Замечание. Для приближенных вычислений можно использовать формулу f (M)  f (M 0)+
f (M 0)+  .
.
Теорема (об инвариантности формы первого дифференциала). Пусть  ,
,  ,
, 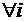
 ,
,  ,
,
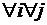
 ;
;  ; (i =1,…, n); (j =1,…, m),
; (i =1,…, n); (j =1,…, m),
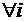
 ;
;  .
.
Тогда df =  =
=  .
.
Доказательство. 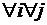

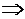
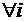
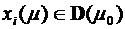
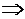
 dxi =
dxi =  . Тогда df =
. Тогда df = 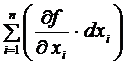 =
=
=  =
=  =
=  =
=
=  =
= 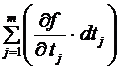 .
.
НЕЯВНАЯ ФУНКЦИЯ
Определение. Пусть есть уравнение  (т.е.
(т.е.  ), ставящее в соответствие каждой точке М одно или несколько значений u, удовлетворяющих этому уравнению. Тогда говорят, что это уравнение неявно определяет одну или несколько функций
), ставящее в соответствие каждой точке М одно или несколько значений u, удовлетворяющих этому уравнению. Тогда говорят, что это уравнение неявно определяет одну или несколько функций  .
.
Теорема (о производной неявной функции). Пусть уравнение  задает неявную функцию
задает неявную функцию  и
и  , где
, где  и
и  . Если имеется окрестность точки
. Если имеется окрестность точки  , такая что
, такая что 
 ,
, 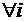

 ,
, 
 ,
,  , то
, то 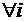
 =
=  .
.
Доказательство (для  ). Пусть переменная х 1 получила приращение
). Пусть переменная х 1 получила приращение  , а остальные переменные
, а остальные переменные  приращений не получили. Это вызвало приращение
приращений не получили. Это вызвало приращение  , такое что
, такое что 
 и
и  . Следовательно,
. Следовательно,  .
.
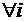
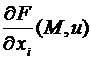
 ,
, 

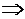
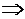

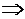
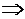
 =
= 
 +0+…+0+
+0+…+0+ 
 +
+ 
 +
+
+0+…+0+ 
 =0
=0 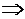
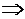
 +
+ 
 +
+  +
+ 