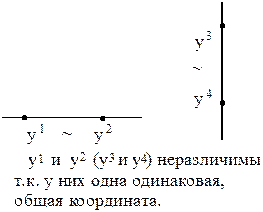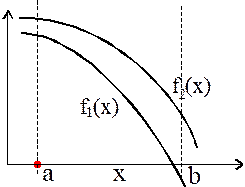Лабораторная работа №12.
Многокритериальные задачи. Построение множеств Парето.
Цель работы: изучение парето-эффективных множеств.
Постановка задачи: Построить множество Парето для
а) заданного множества оценок 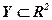 ;
;
б) заданного множества решений 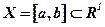 и двух критериев f1(x), f2(x).
и двух критериев f1(x), f2(x).
Теоретические сведения к выполнению лабораторной работы.
Пусть 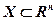 множество допустимых решений, качество которых оценивается с помощью векторного критерия качества
множество допустимых решений, качество которых оценивается с помощью векторного критерия качества
 ;
;
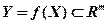 - множество оценок, состоящее и оценок
- множество оценок, состоящее и оценок 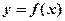 ;
;  - отношение предпочтения ЛПР (лица, принимающего решения), которое будем использовать как для сравнения различных решений, так и их оценок, ≥ - отношение «больше либо равно, но не совпадает».
- отношение предпочтения ЛПР (лица, принимающего решения), которое будем использовать как для сравнения различных решений, так и их оценок, ≥ - отношение «больше либо равно, но не совпадает».
Рассмотрим сначала множество оценок Y.
Сильная Аксиома Парето. Если для двух оценок 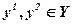 выполняется соотношение y1 ³ y2, то
выполняется соотношение y1 ³ y2, то  .
.
Аксиома Парето позволяет перейти от абстрактного отношения предпочтения  к вполне конкретному и легко проверяемому отношению ≥.
к вполне конкретному и легко проверяемому отношению ≥.
Оценку y*, будем называть парето-оптимальной (в сильном смысле), если не существует такой оценки  , что y³ y*.
, что y³ y*.
Через P(Y) будем обозначать множество оптимальных оценок на Y.
Рассмотрим вопрос о геометрической интерпретации парето-оптимальных точек и построении их множества P(Y) при m=2. Прежде всего отметим, что если y1 ³ y2, то геометрически это означает, что оценка y1 находится в створе угла, построенного по точке y2 (внутри угла или на его сторонах и не совпадает с y2):

Рис. 1. Геометрическая интерпретация отношения y1 ³ y2.
Отсюда вытекает, что парето-оптимальная оценка – это такая оценка, что в створ построенного по ней угла, не попадают другие оценки из множества Y. Поэтому внутренняя точка множества Y не может быть парето-оптимальной: в створ угла, построенной по внутренней точке, обязательно попадают другие оценки. Таким образом, парето-оптимальная оценка – граничная точка множества оценок. При этом это не любая граничная точка, а «северо-восточная» граничная точка:
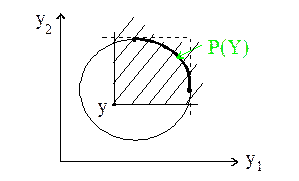
Рис. 2. Геометрическая интерпретация множества P(Y).
Если множество Y строго выпуклое, то P(Y) строится достаточно просто. В случае невыпулого множества или множества со сложной конфигурацией границы появляются проблемы. Их «создают» оценки, лежащие на одной вертикали или одной горизонтали. В соответствии с сильной аксиомой Парето из двух оценок, лежащих на одной горизонтали, «лучшей» является та, которая находится правее. Аналогично, из двух оценок, лежащих на одной вертикали, лучшей является та, которая находится выше. Поэтому парето-оптимальные в сильном смысле оценки не могут находиться на горизонтальных или вертикальных промежутках границы (точнее, внутри этих промежутков). Они могут располагаться только на концах таких промежутков (на правом конце горизонтального промежутка или верхнем конце вертикального промежутка). Примеры построения Парето-оптимальных множеств для множеств со сложной границей приведены на рис. 3.
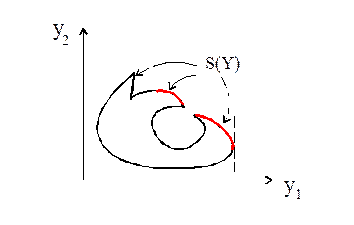
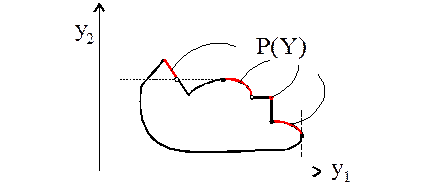

Рис 3. Построение Парето-оптимальных множеств для множеств со
сложной конфигурацией границы.
Слабая Аксиома Парето. Если для двух оценок 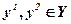 выполняется соотношение y1 > y2, то
выполняется соотношение y1 > y2, то 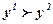 .
.
Оценку y*, будем называть парето-оптимальной (в слабом смысле), если не существует такой оценки 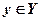 , что y> y*.
, что y> y*.
Через S(Y) будем обозначать множество парето-оптимальных оценок (в слабом смысле) на Y.
Слабая аксиома Парето отличается от сильной всего лишь одним значком: вместо отношения «больше либо равно, но не совпадает» (≥) используется отношение «больше» (>). Однако смена операции отношения существенно влияет в ряде случаев на построение множества парето-оптимальных точек.
Рассмотрим сначала отношение y1 > y2 и его геометрическую интерпретацию. Оценка y1 «лучше» y2 в том случае, если она находится внутри угла, построенного по точке y2. Она не может находиться на стороне угла, так как с точки зрения отношения «>» такие точки являются неразличимыми с y2 (см. рис. 4).
|
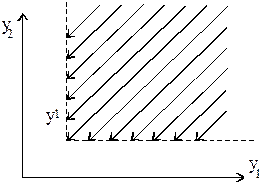
Рис. 4. Геометрическая интерпретация отношения y1 > y2.
На рис. 5 приведен пример, который наглядно иллюстрирует разницу между множествами P(Y) и S(Y).
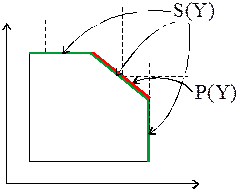
Рис. 5. Геометрическая интерпретация множеств P(Y) и S(Y).
Более сложный случай представлен на рис. 6.
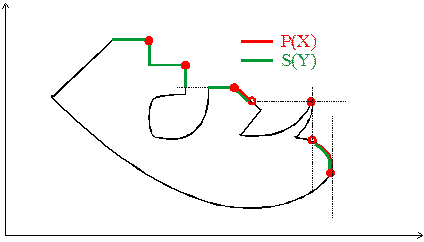
Рис. 6. Различие между P(X) и S(Y) в случае множества со сложной границей.
Вернемся теперь к множеству решений X. В терминах решений сильная и слабая аксиомы Парето формулируются следующим образом:
Сильная Аксиома Парето. Если для двух решений 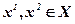 выполняется соотношение f (x1) ³f( x2), то
выполняется соотношение f (x1) ³f( x2), то 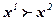 .
.
Слабая Аксиома Парето. Если для двух решений 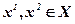 выполняется соотношение f (x1) >f( x2), то
выполняется соотношение f (x1) >f( x2), то 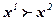 .
.
Решение x*, будем называть парето-оптимальным (в сильном смысле), если не существует такого другого решения 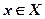 , что f(x)³ f(x*).
, что f(x)³ f(x*).
Решение x*, будем называть парето-оптимальным (в слабом смысле), если не существует такого другого решения 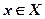 , что f(x)> f(x*).
, что f(x)> f(x*).
Дадим геометрическую интерпретацию этим аксиомам и определениям при n=1 и m=2 (одна переменная, 2 критерия).
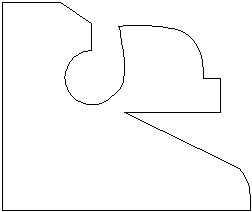
Вначале рассмотрим сильную аксиому. Отношение f(x1)³ f(x2) выполняется только в том случае, если значение обоих критериев в точке x1 не меньше значений критериев в точке x2. Это означает, что парето-оптимальные решения не могут находиться на промежутках монотонного возрастания или убывания обоих критериев. Поэтому в примере, представленном на рис. 7 а), множество P(X)={b}, а на рисунке 7 б) - P(X)={а}.
| |||
| |||
Рис. 7. Парето-оптимальные множества в случае одинакового поведения критериев.
В то же время промежутки, на которых критерии ведут себя по-разному, являются подозрительными на парето-оптимальность. В простейшем случае (см. рис. 8) P(X)=X.

Рис. 8. Парето-оптимальное множества в случае разного поведения
монотонных критериев.
На рис. 9 приведены примеры, когда один из критериев является монотонным, а второй - немонотонным.
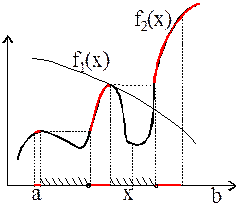
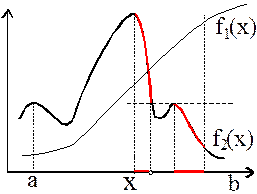
Рис. 9. Парето-оптимальные множества в случае, если один из критериев монотонен.
Алгоритм построения множества P(X), если один из критериев монотонен, можно описать следующим образом. Допустим, что f1(x) монотонно убывает.
1. По графику f2(x) найдем подмножество значений Xв, на котором функция f2(x) монотонно возрастает (т.е. удалим из множества X промежутки, на которых f2(x) убывает и образует впадины). Максимальное из всех подмножеств Xв и будет парето-оптимальным множеством решений.
2. Исследуем концы соседних отрезков, образующих парето-оптимальное множество. Из двух смежных концов выбирается тот, у которого один из критериев имеет большее значение (значения по другому из критериев у таких точек одинаковы). Эта ситуация иллюстрируется на рис. 10
Рис. 10. Анализ точек на концах отрезков парето-оптимальных множеств.
В том случае, если оба из критериев немонотонны, дать какие-либо простые правила по построению парето-оптимальных точек невозможно. Рекомендуется переходить к оценкам и проводить исследование парето-оптимальных точек на множестве оценок.
Множество слабо-парето-оптимальных точек S(X) в рассматриваемых случаях совпадает или почти совпадают с P(X). Отличие только на концах отрезков. В силу свойств отношения “>” смежные точки на концах отрезков неразличимы. Поэтому S(X) содержит концы всех своих отрезков.
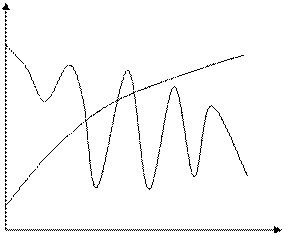
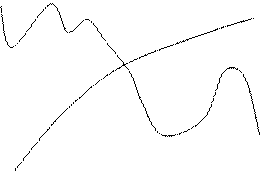
2. Варианты заданий к лабораторной работе
| № | К заданию а) | К заданию б) |
| 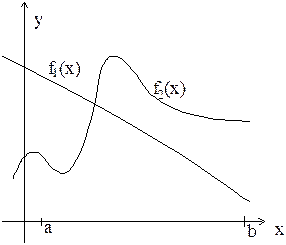
| |

| 
| |
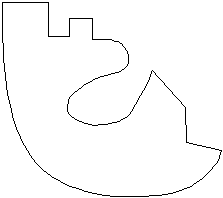
| 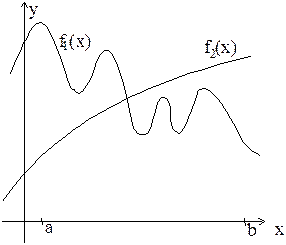
| |
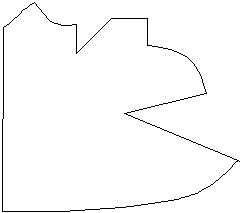
| 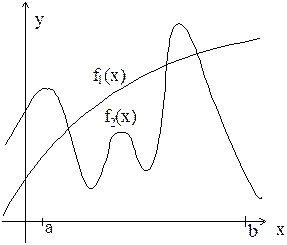
| |
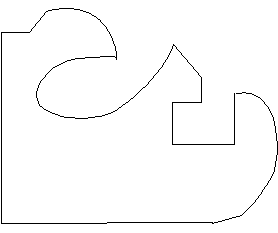
|
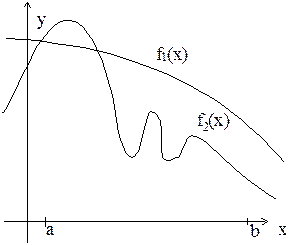
| |
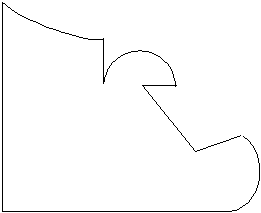
|
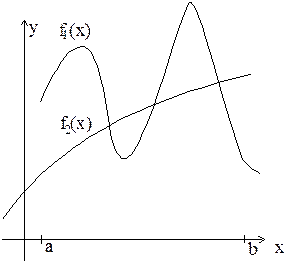
|
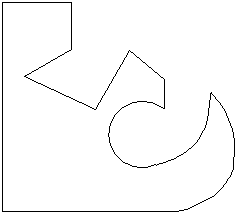
|
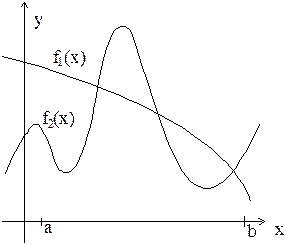
| |
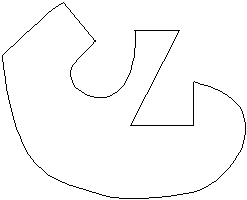
|
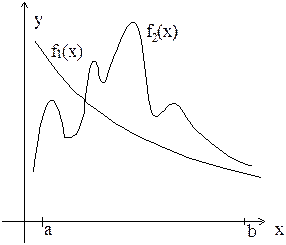
| |
|
|
|
| |
|
| |

|
|
|
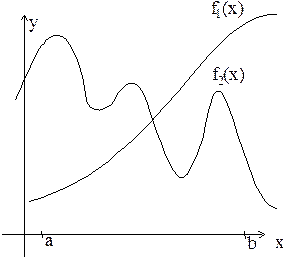
| |

| 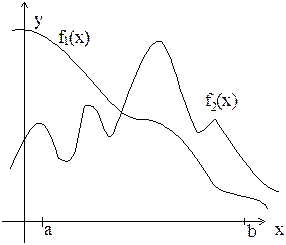
| |
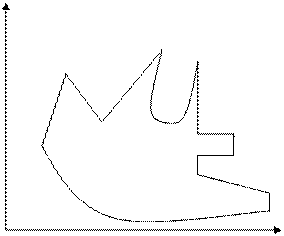
| 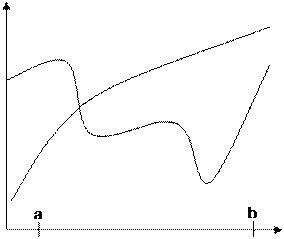
|

 
| 
| |
 
| 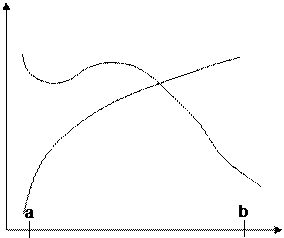
| |
 
| 
| |
 
| 
| |
 
| 
| |
 
|  
| |
 
|   
| |
 
| 
| |
 
| 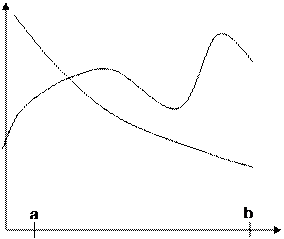
| |
 
|    
| |
 
| 
| |
 
| 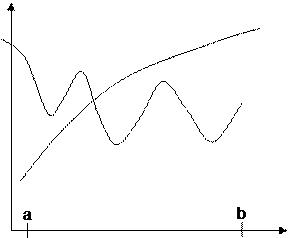
|
3. Требования к отчету по лабораторной работе. Отчет должен включать:
· титульный лист установленной формы.
· постановку задачи с конкретизированным данными.
· рисунки множеств с выделенными на них оптимальными точками по Парето.