Первообразная. Неопределённый интеграл и его свойства
Пусть функция f(x) задана на некотором множестве X. Тогда функция
F(x), определенная на этом множестве, называется первообразной функции
f(х), если она дифференцируема для любых  и F'(x) = f(x) для всех
и F'(x) = f(x) для всех
 .
.
Если F(x) - одна из первообразных функции f(x) на множестве X, то
любая другая первообразная функции f(x) имеет вид F(x) + c, где с - некоторая постоянная.
Совокупность F(x) + с всех первообразных функции f(x) на множестве
X называется неопределенным интегралом от функции f(x) и обозначается
 где
где 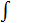 - знак интеграла, f(x) - подынтегральная функция, f(x)dx-
- знак интеграла, f(x) - подынтегральная функция, f(x)dx-
подынтегральное выражение. Таким образом.
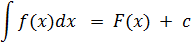
Операция нахождения всех первообразных функции f(x) называется
интегрированием этой функции.
Перечислим основные свойства неопределенного интеграла (правила интегрирования):
Функция F (х) называется первообразной функцией для функции f (x) на промежутке

Интеграл от основных элементарных функций


Непосредственное интегрирование.
Непосредственным интегрированием называют приведение данного интеграла к алгебраической сумме более простых интегралов, используя основные правила интегрирования (свойства 4 и 5 неопределенного интеграла), тождественные преобразования подынтегральной функции с целью получения выражений, имеющихся в таблице основных интегралов.
Интегрируя функции, содержащие переменную в знаменателе дроби или под знаком радикала, нужно вводить степень с отрицательным или дробным показателем, привести подынтегральное выражение к виду какого-либо табличного интеграла.
При интегрировании произведения в ряде случаев полезно предварительно раскрыть скобки.
Пример 1


Пример 2

Решение.
Данный интеграл не является табличным. Представим подынтегральную функцию в виде

Теперь применим формулу 3 таблицы основных интегралов и получим:


Пример 3
Найти интеграл

Пример 4
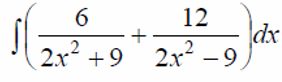


Пример 5

Пример 6
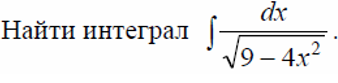
Решение.
Данный интеграл приведем к табличному следующим образом:


Пример 7




Пример 8
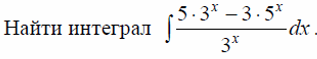
Решение. Используя правило 5 интегрирования и формулу 7 таблицы
интегралов, получим:


Пример 9

Пример 10

Решение. Применяя правило 5 интегрирования и формулы 3, 6, 5
таблицы интегралов, получим:

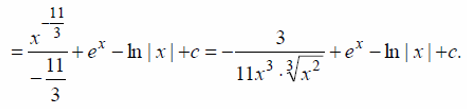
Интегрирование путем подведения под знак дифференциала
И методом подстановки
Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом случае пользуются методом подстановки (методом замены переменной интегрирования).
Сущность этого метода заключается в том, что путем введения новой переменной удается свести данный интеграл к новому интегралу, который сравнительно легко берется непосредственно.
Для интегрирования методом подстановки можно использовать
следующую схему:
1) часть подынтегральной функции надо заменить новой переменной:
2) найти дифференциал от обеих частей замены:
3) все подынтегральное выражение выразить через новую переменную
(после чего должен получиться табличный интеграл);
4) найти полученный табличный интеграл:
5) сделать обратную замену.
Методом подстановки или методом замены переменной. При применении этого метода используют подстановки двух видов:





Пример 1

Решение. Этот интеграл можно найти и не производя замены переменной. Здесь достаточно развернуть выражение  по формуле бинома
по формуле бинома
Ньютона и применить почленное интегрирование. Однако этот способ связан с большим количеством вычислений. При помощи замены переменной можно сразу свести данный интеграл к табличному.
Введем 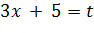
тогда


Отсюда получаем
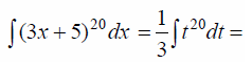

Пример 2

Пример 3


Пример 4
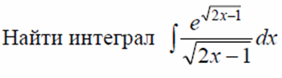
Пример 5

Решение.
Сведем этот интеграл к табличному интегралу

Преобразуем интеграл

Введем новую переменную

Тогда

Откуда

Окончательно получаем

Интегрирование по частям
Одним из эффективных методов интегрирования является метод интегрирования по частям. Этот метод чаше всего применяется для интегрирования некоторых трансцендентных функций (например, ln x, arcsin x, arctg x), а также произведений алгебраических и трансцендентных функций. Суть его состоит в следующем.
Если 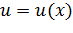 и
и  - непрерывно дифференцируемые на некотором интервале функции, кроме того, на этом интервале существует интеграл
- непрерывно дифференцируемые на некотором интервале функции, кроме того, на этом интервале существует интеграл  , то на нем существует интеграл
, то на нем существует интеграл  и имеет место формула
и имеет место формула
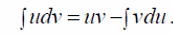


Эта формула часто применяется, когда подынтегральной функцией является:
• логарифмическая или обратная тригонометрическая функция:
• произведение каждой из этих функций на алгебраическую:
• произведение, содержащее алгебраические, тригонометрические,
показательные функции и др.
При использовании этой формулы подынтегральное выражение нужно разбивать на два множителя u и dv таким образом, чтобы интегрирование выражений dv и vdu было более простым, чем интегрирование исходного выражения udv.
Формула интегрирования по частям может применяться неоднократно.
Некоторые рекомендации:

Интегрирование по частям иногда приводит к интегралу, совпадающему с исходным или сводящемуся к нему. В этом случае интеграл находится из получающегося относительно исходного интеграла уравнения.
Пример 1
Вычислить интеграл

Решение. Положим здесь

откуда



Пример 2
Вычислить интеграл

Решение. Положим здесь

откуда

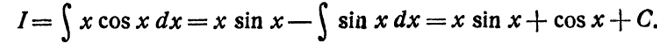
Посмотрим на этом примере, к каким результатам приводит удачный выбор множителей и и dv.
Положим

Откуда

Тогда

Интеграл не упростился, а усложнился.
Пример 3
Вычислить интеграл

Пример 4
Вычислить интеграл

Решение. Положим здесь

откуда
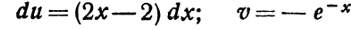

Последний интеграл опять проинтегрируем по частям.
Положим

Откуда
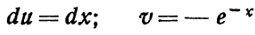
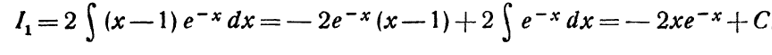
Окончательно получим
