Центральным аппаратом в любой химико-технологической системе, включающей целый ряд машин и аппаратов, соединенных между собой различными связями, является химический реактор - аппарат, в котором протекает химический процесс. Выбор типа, конструкции и расчет химического реактора, создание системы управление его работой – одна из важных задач химической технологии.
Как и в случае других аппаратов, используемых в химической промышленности (теплообменных, массообменных и др.), для изучения, расчета и проектирования химических реакторов применяется метод моделирования.
Под математической моделью понимается некоторое упрощенное изображение процесса в реакторе, которое сохраняется наиболее существенные свойства реального объекта и передает их в математической форме. В зависимости от постановленной задачи математическая модель учитывает разное число признаков объекта и поэтому модель может быть широкой и узкой.
Модель реактора идеального вытеснения
Реакторы вытеснения – трубчатые аппараты, имеющие вид удлиненного канала. В трубчатых реакторах перемещение имеет локальный характер и вызывается неравномерностью распределения скорости потока и ее флуктуациями, а также завихрениями. Реакторы вытеснения бывают двух видов: идеального и полного вытеснения.
Идеально вытеснение предполагает, что любое количество реагентов и продуктов через реактор перемещается как твердый поршень, и по длине реактора (в пространстве) в соответствии с особенностями реакции и сопровождающих ее физических явлений устанавливается определенное распределение концентраций участников реакции, температуры и других параметров.К реакторам идеального вытеснения относятся те аппараты, в которых отсутствует радиальное и продольное перемешивание.
|
|
Материальный баланс
Материальный баланс – вещественное выражение закона сохранения массы вещества, согласно которому по всякой замкнутой системе масса веществ, вступивших во взаимодействие, равна массе веществ, образовавшихся в результате взаимодействия. Применительно к материальному балансу любого технологического процесса это означает, что масса веществ, поступивших на технологическую операцию – приход, равна массе полученных веществ – расходу. Материальный баланс составляют по уравнению основной суммарной реакции с учетом параллельных и побочных реакций.
Материальный баланс непрерывно действующих проточных реакторов составляется, как правило, для установившегося (стационарного) режима, при котором общая масса веществ, поступивших в аппарат за данный период времени, равна массе веществ, вышедших из аппарата. Количество же всех веществ в аппарате постоянно, т. е. накопления или убыли суммарного количества веществ не происходит.[3]
Составим материальный баланс реактора идеального вытеснения.
dV ZNA
x x+dx
Реактор представляет собой длинный канал, через который реакционная смесь движется в поршневом режиме. Изменение концентрации происходит по длине. Выделим элементарный объем dV, для которого считается материальный баланс, где ZNA-концентрация ключевого реагента.
[кг/c]=[(м3/с)∙(м3/кмоль)∙(кг/кмоль)]
- расход
-массовый расход химической реакции
[кг/с]=[(кмоль/м3∙с)∙(м3)∙(кг/кмоль)
|
|
-массовый расход на убыль
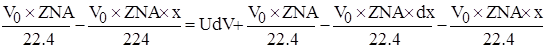
- объем реактора
[м3]=[(м3/c)∙(c)]
- уравнение материального баланса для реактора, работающего в режиме идеального вытеснения.
- время пребывания реакционной смеси в реакторе для получения заданной степени превращения x. Из этого уравнения можно рассчитать объем реактора.
Тепловой баланс
Hfp Hch
Hfr Hт/o
-теплота физического прихода, где Cp-теплоемкость.
[кДж/с]=[(м3/c)∙(кДж/м3/град)∙(град)]
- теплота физического расхода.
[кДж/с]=[(м3/c)∙(кДж/м3/град)∙(град)]
- теплота химической реакции.
[кДж/c]=[(кмоль/м3∙c)∙(кДж/кмоль)∙(м3)]
-теплота теплообменника,
[кДж/c]=[(кДж/м2∙град∙с)∙(м2/м3)∙(град)∙(м3)]
Где К-коэффициент теплопередачи, определяющийся по следующей формуле
,
Где d-толщина стенки;
α1, α2 - коэффициент теплоотдачи с наружной и внутренней поверхностях соответственно;
λ – коэффициент теплопроводности
Приход:
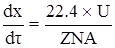
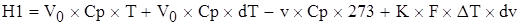
Расход:
По закону сохранения энергии:
-
уравнение политермы, в котором учитывается часть теплоты химической реакции, идущей на изменение температур в химической реакции, и часть, уходящая на теплоту, которую уводит теплообменник.
В адиабатическом режиме теплообменник отсутствует:
- уравнение адиабаты.
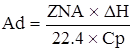- адиабатический коэффициент.
Физический смысл адиабатического коэффициента: на столько градусов изменится температура реакционной смеси, если степень превращения будет равна 1, то есть, если ключевой реагент прореагировал полностью.