Занятие №63-64.
Тема: Формулы приведения.
Цель: Научиться применять формулы приведения при нахождении значений тригонометрических функций любых углов и применять их при преобразовании тригонометрических выражений.
Ход занятия.
Проверка домашней работы.
Почему-то многие из вас решили, что конспект писать не обязательно?! А ведь практически на каждом занятии вводятся новые тригонометрические формулы, правила и т. д. Впредь прошу основные положения конспекта записывать, а домашние упражнения решать самостоятельно, а не списывать, причём с ошибками, а то почти все работы писаны как под копирку!
2. Перечень вопросов, рассматриваемых в теме:
· формулы приведения;
- мнемоническое правило для формул приведения;
- преобразование тригонометрических выражений на основе использования формул приведения;
- вычисление значений тригонометрических выражений на основе формул приведения;
- доказательство тригонометрические тождества на основе формул приведения;
·
· 3.Теоретический материал для самостоятельного изучения
Для вычисления значений тригонометрических функций углов больше 90⁰  используют формулы приведения. Они позволяют синус, косинус, тангенс и котангенс различных углов приводить к острым углам.
используют формулы приведения. Они позволяют синус, косинус, тангенс и котангенс различных углов приводить к острым углам.
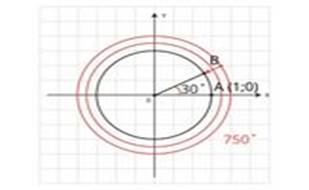
Пример: Вычислить sin750⁰ и cos750⁰  .
.
Представим число 750⁰=360⁰ 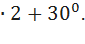

 .
.
Рассмотрим точку А(1;0) на единичной окружности. При повороте вокруг начала координат на угол 750⁰  она сделает 2 полных оборота по 360⁰
она сделает 2 полных оборота по 360⁰  и ещё повернётся на угол 30⁰
и ещё повернётся на угол 30⁰  . Переместится в точку В, в которую могла бы попасть, сделав поворот на угол 30⁰
. Переместится в точку В, в которую могла бы попасть, сделав поворот на угол 30⁰  . Значит, sin750⁰=sin30⁰=
. Значит, sin750⁰=sin30⁰= 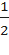 , а cos750⁰=cos30⁰=
, а cos750⁰=cos30⁰= 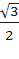 .
.
Таким образом, справедливы равенства sin750⁰=sin(360⁰ 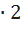 +30⁰)=sin30⁰, аналогично
+30⁰)=sin30⁰, аналогично
Cos750⁰=cos(360⁰ 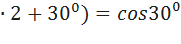
Количество полных оборотов по 360  или по 2
или по 2 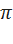
 может выражаться любым целым числом k, как положительным, так и отрицательным и нулём. При повороте точки А(1;0) на угол2
может выражаться любым целым числом k, как положительным, так и отрицательным и нулём. При повороте точки А(1;0) на угол2 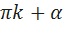 , где k
, где k 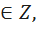
 получается та же самая точка, что при повороте на угол
получается та же самая точка, что при повороте на угол 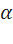

Для вычисления углов больше 90⁰  используют формулы приведения. Они позволяют синус, косинус, тангенс и котангенс различных углов приводить к острым углам.
используют формулы приведения. Они позволяют синус, косинус, тангенс и котангенс различных углов приводить к острым углам.
Справедливы равенства:
Sin(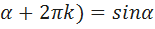 , где k
, где k 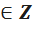 , cos(
, cos(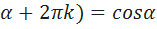 , где k
, где k 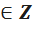

Пусть точка А(1;0) переместилась в точку В1 при повороте на угол 135⁰  и в точку В при повороте на угол 45⁰
и в точку В при повороте на угол 45⁰  (рис. 2).
(рис. 2).

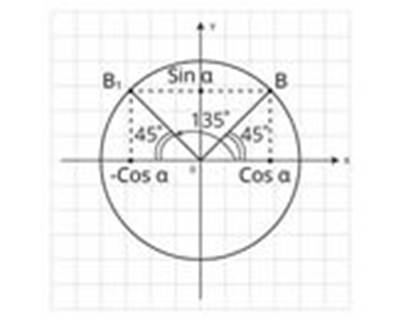

Рисунок 2 – точки А, В, В1 на единичной окружности
Запишем 135⁰  в виде: 180⁰ - 45⁰. На единичной окружности точки В1 и В симметричны относительно оси Оу, значит их ординаты (синусы) равны, абсциссы (косинусы)- противоположные числа.
в виде: 180⁰ - 45⁰. На единичной окружности точки В1 и В симметричны относительно оси Оу, значит их ординаты (синусы) равны, абсциссы (косинусы)- противоположные числа.
Поэтомуsin135⁰=sin(180⁰- 45⁰)=sin45⁰= 
 , а cos135⁰=cos(180⁰- 45⁰)=-cos45⁰=-
, а cos135⁰=cos(180⁰- 45⁰)=-cos45⁰=- 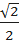
 .
.
А так как 180⁰= 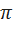
 , то справедливы формулы sin(
, то справедливы формулы sin(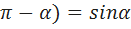 , cos(
, cos(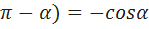
 .
.
Используя формулы сложения, докажем следующие формулы приведения:
Sin( –
– 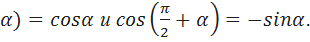

Воспользуемся формулой синуса разности и косинуса суммы:  sin(
sin(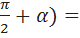 sin
sin  cosα+
cosα+
Cos  sinα=1
sinα=1 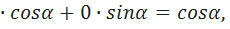 и cos(
и cos(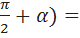 cos
cos  cos
cos 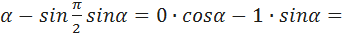
- sin 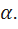 Формулы доказаны.
Формулы доказаны.
Аналогично доказываются и другие формулы приведения и все они связаны следующим правилом: Если в формуле приведения угол равен 90⁰ 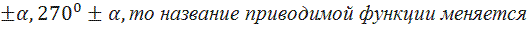 (синус на косинус, тангенс на котангенс и наоборот), а если угол равен 180⁰
(синус на косинус, тангенс на котангенс и наоборот), а если угол равен 180⁰ 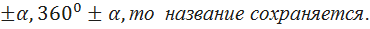 Знак перед приведённой функцией ставится такой, каков знак приводимой функции в соответствующей четверти, считая угол
Знак перед приведённой функцией ставится такой, каков знак приводимой функции в соответствующей четверти, считая угол 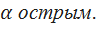
Это правило можно записать тремя словами: